北师大版九年级数学上册 4.6利用相似三角形测高 同步学案(无答案)
文档属性
| 名称 | 北师大版九年级数学上册 4.6利用相似三角形测高 同步学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 60.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 00:00:00 | ||
图片预览

文档简介
4.6利用相似三角形测高
【学习目标】:
1. 掌握几种测量旗杆高度的方法与原理
2. 解决一些较简单的相关生活实际问题
【学习重点】: 通过设计测量旗杆高度的方案,学会将实物图形抽象成几何图形的方法.
【学习难点】:体会将实际问题转化成数学模型的转化思想.
【学习过程】:
【一、预学】:
1、提出问题,创设情境:
问题(1):1. 相似三角形的性质:相似三角形的对应角_________,对应边_________;
2.相似三角形的判定:①___________________的两个三角形相似; ②________________且___________的两个三角形相似;③______________________的两个三角形相似;
目标导引,预学探究:
问题(2):学校操场上的国旗旗杆的高度是多少?你有什么办法测量?
【二、研学】(合作发现,交流展示)
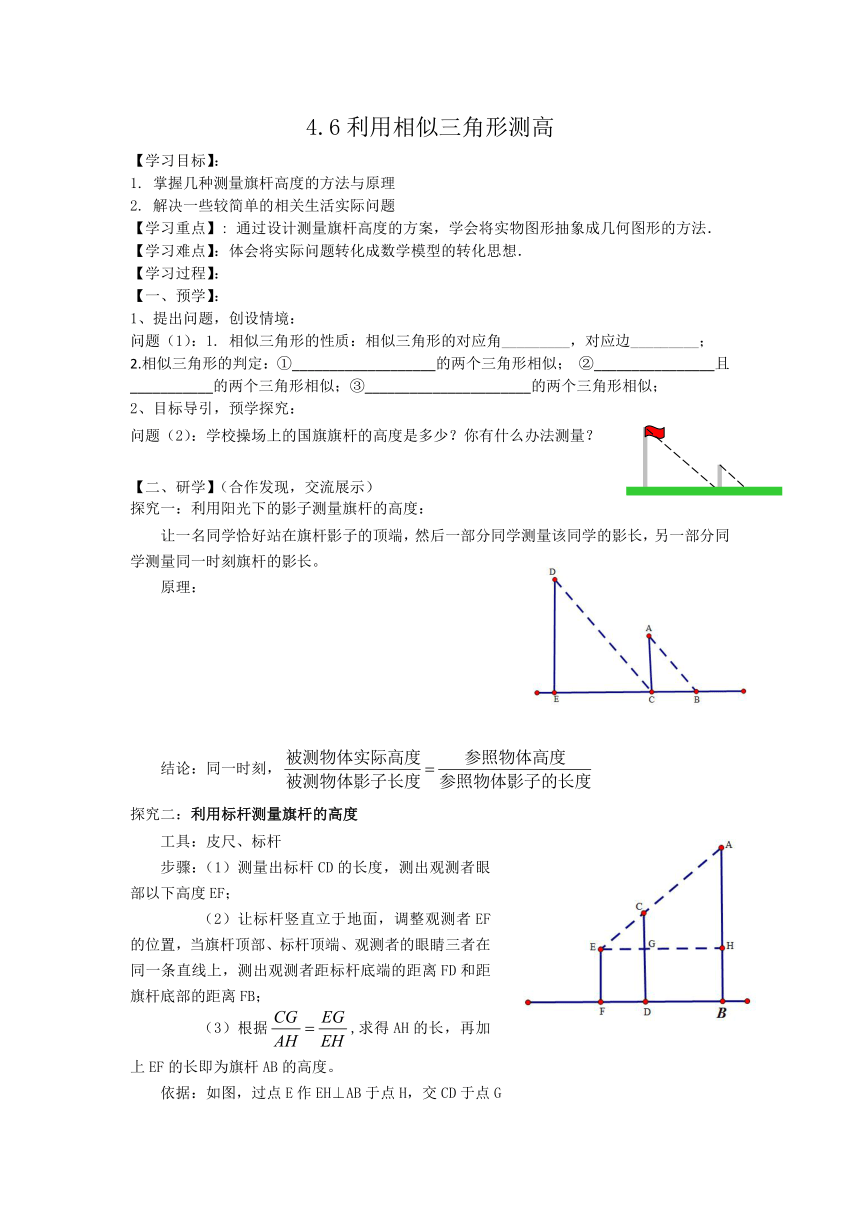
探究一:利用阳光下的影子测量旗杆的高度:
让一名同学恰好站在旗杆影子的顶端,然后一部分同学测量该同学的影长,另一部分同学测量同一时刻旗杆的影长。
原理:
结论:同一时刻,
探究二:利用标杆测量旗杆的高度
工具:皮尺、标杆
步骤:(1)测量出标杆CD的长度,测出观测者眼部以下高度EF;
(2)让标杆竖直立于地面,调整观测者EF的位置,当旗杆顶部、标杆顶端、观测者的眼睛三者在同一条直线上,测出观测者距标杆底端的距离FD和距旗杆底部的距离FB;
(3)根据,求得AH的长,再加上EF的长即为旗杆AB的高度。
依据:如图,过点E作EH⊥AB于点H,交CD于点G
∵CD∥AB ∴∠ECG=∠EAH
∵∠CEG=∠AEH ∴△ ∽△
∴
∵EG=FD,EH=FB,CG=CD-GD=CD-EF,
且FD,FB,CD,EF可测
∴可求AH的长度
∴AB=AH+HB=AH+EF
探究三:利用镜子的反射杆测量旗杆的高度
工具:皮尺、镜子
步骤:(1)在观测者与旗杆之间放一面镜子,在镜子上做一个标记;
(2)测出观测者眼睛到地面的距离;
(3)观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合,此时测出镜子上标记O到人脚底D的距离OD及镜子上的标记O到旗杆底部的距离OB;
(4)把测得的数据代入,即可求得旗杆的高度AB。
依据:在△COD与△AOB中
∵∠COD=∠AOB,∠CDO=∠ABO=90°
∴△ ∽△ ∴
∵CD,OD,OB皆可测得 ∴ AB可求。
探究x:
【三、评学】:
积累巩固:
1、基础练习
高4m的旗杆在水平地面上的影子长为6m,此时测得附近一个建筑物的影子长24m,求该建筑物的高度。
2.旗杆的影子长为6m,同时测得旗杆顶端到其影子顶端的距离是10m,如果此时附近一座纪念塔的影子长30m,那么这座纪念塔有多高?
2、拓展延伸:
1.如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1cm.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,求窗户的高度.
【课堂小结】:
通过本课学习,你掌握了哪些知识?获得了哪些技能?还存在什么疑问?
【学习目标】:
1. 掌握几种测量旗杆高度的方法与原理
2. 解决一些较简单的相关生活实际问题
【学习重点】: 通过设计测量旗杆高度的方案,学会将实物图形抽象成几何图形的方法.
【学习难点】:体会将实际问题转化成数学模型的转化思想.
【学习过程】:
【一、预学】:
1、提出问题,创设情境:
问题(1):1. 相似三角形的性质:相似三角形的对应角_________,对应边_________;
2.相似三角形的判定:①___________________的两个三角形相似; ②________________且___________的两个三角形相似;③______________________的两个三角形相似;
目标导引,预学探究:
问题(2):学校操场上的国旗旗杆的高度是多少?你有什么办法测量?
【二、研学】(合作发现,交流展示)
探究一:利用阳光下的影子测量旗杆的高度:
让一名同学恰好站在旗杆影子的顶端,然后一部分同学测量该同学的影长,另一部分同学测量同一时刻旗杆的影长。
原理:
结论:同一时刻,
探究二:利用标杆测量旗杆的高度
工具:皮尺、标杆
步骤:(1)测量出标杆CD的长度,测出观测者眼部以下高度EF;
(2)让标杆竖直立于地面,调整观测者EF的位置,当旗杆顶部、标杆顶端、观测者的眼睛三者在同一条直线上,测出观测者距标杆底端的距离FD和距旗杆底部的距离FB;
(3)根据,求得AH的长,再加上EF的长即为旗杆AB的高度。
依据:如图,过点E作EH⊥AB于点H,交CD于点G
∵CD∥AB ∴∠ECG=∠EAH
∵∠CEG=∠AEH ∴△ ∽△
∴
∵EG=FD,EH=FB,CG=CD-GD=CD-EF,
且FD,FB,CD,EF可测
∴可求AH的长度
∴AB=AH+HB=AH+EF
探究三:利用镜子的反射杆测量旗杆的高度
工具:皮尺、镜子
步骤:(1)在观测者与旗杆之间放一面镜子,在镜子上做一个标记;
(2)测出观测者眼睛到地面的距离;
(3)观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合,此时测出镜子上标记O到人脚底D的距离OD及镜子上的标记O到旗杆底部的距离OB;
(4)把测得的数据代入,即可求得旗杆的高度AB。
依据:在△COD与△AOB中
∵∠COD=∠AOB,∠CDO=∠ABO=90°
∴△ ∽△ ∴
∵CD,OD,OB皆可测得 ∴ AB可求。
探究x:
【三、评学】:
积累巩固:
1、基础练习
高4m的旗杆在水平地面上的影子长为6m,此时测得附近一个建筑物的影子长24m,求该建筑物的高度。
2.旗杆的影子长为6m,同时测得旗杆顶端到其影子顶端的距离是10m,如果此时附近一座纪念塔的影子长30m,那么这座纪念塔有多高?
2、拓展延伸:
1.如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面的距离BC=1cm.已知某一时刻BC在地面的影长CN=1.5m,AC在地面的影长CM=4.5m,求窗户的高度.
【课堂小结】:
通过本课学习,你掌握了哪些知识?获得了哪些技能?还存在什么疑问?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
