有理数的乘法[上学期]
图片预览






文档简介
课件24张PPT。郁文中学yujianqing 制作有理数乘法教学目标:
1.经历探索有理数乘法法则的过程,发展观察、归纳、
猜测、验证等能力。
2.能运用法则进行简单的有理数乘法运算。
3.培养学生的语言表达能力,通过合作学习,调动学
生学习的积极性,增强 学习数学的自信心
重点: 会利用法则进行简单的有理数乘法运算。
难点: 法则的推导。
我们在小学已经熟悉正数和0的运算,
例如:
那么引入负数之后,怎样进行有理数的乘法运算呢? 比如 (-2) ×(+3) =?
(-5) ×(- 4) =?
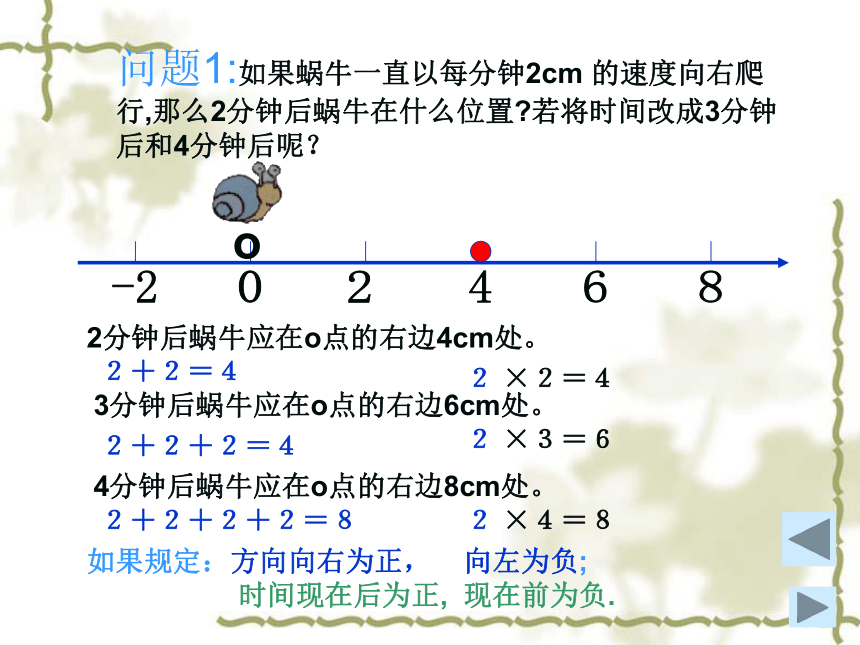
…情境:如下图,一只蜗牛沿着直线L爬行,它现在的位置恰好在 L上的OL问题1:如果蜗牛一直以每分钟2cm 的速度向右爬行,那么2分钟后蜗牛在什么位置?若将时间改成3分钟后和4分钟后呢? o2分钟后蜗牛应在o点的右边4cm处。3分钟后蜗牛应在o点的右边6cm处。4分钟后蜗牛应在o点的右边8cm处。2+2=42 ×2=42+2+2=42 ×3=62+2+2+2=82 ×4=8如果规定:方向向右为正, 向左为负;
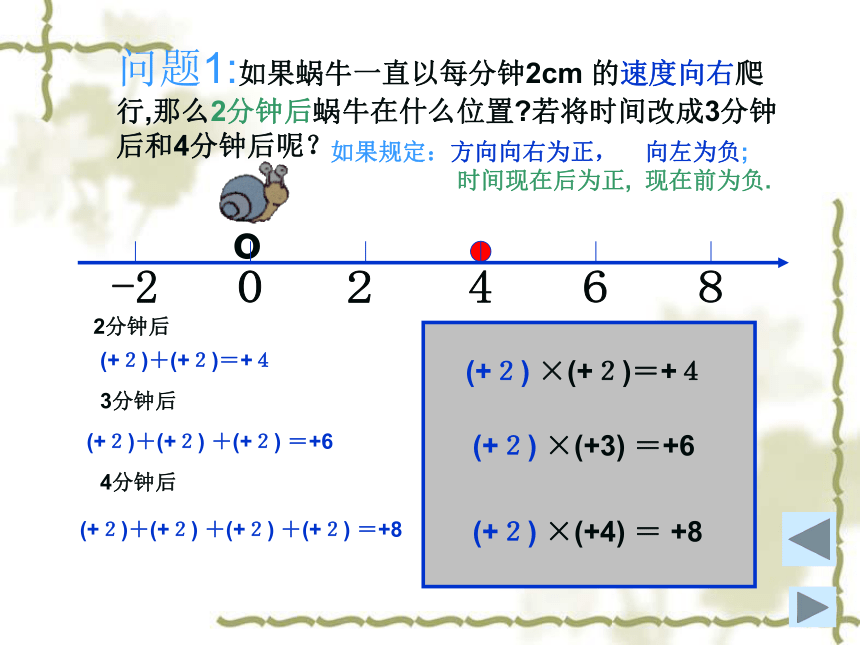
时间现在后为正, 现在前为负.问题1:如果蜗牛一直以每分钟2cm 的速度向右爬行,那么2分钟后蜗牛在什么位置?若将时间改成3分钟后和4分钟后呢? o2分钟后(+2)+(+2)=+4(+2) ×(+2)=+43分钟后(+2)+(+2) +(+2) =+6(+2) ×(+3) =+64分钟后(+2)+(+2) +(+2) +(+2) =+8(+2) ×(+4) = +8如果规定:方向向右为正, 向左为负;
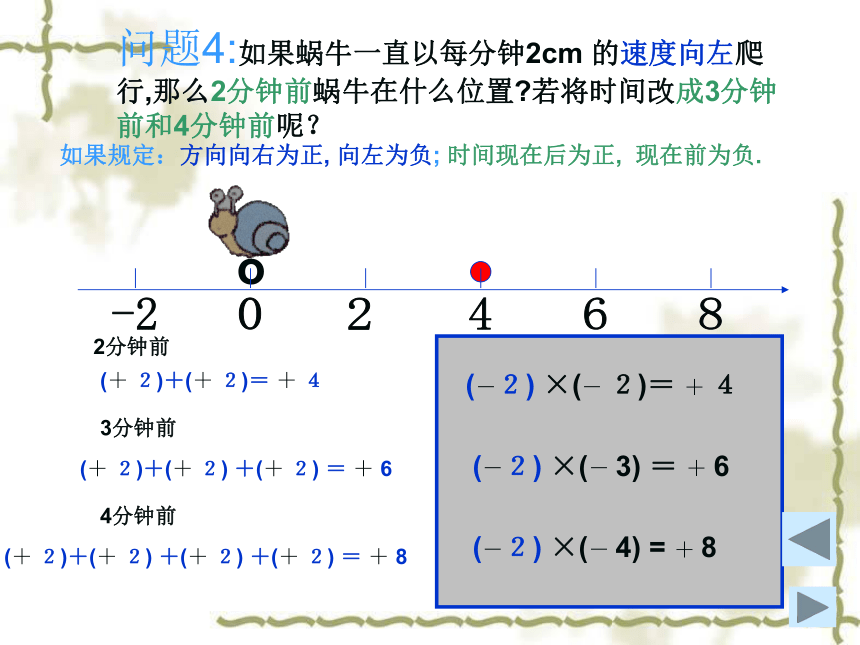
时间现在后为正, 现在前为负.问题2:如果蜗牛一直以每分钟2cm 的速度向左爬行,那么2分钟后蜗牛在什么位置?若将时间改成3分钟后和4分钟后呢? o2分钟后(-2)+(-2)=-4(-2) ×(+2)=-43分钟后(-2)+(-2) +(-2) =-6(-2) ×(+3) =-64分钟后(-2)+(-2) +(-2) +(-2) =-8(-2) ×(+4) =-8如果规定:方向向右为正, 向左为负; 时间现在后为正, 现在前为负.问题3:如果蜗牛一直以每分钟2cm 的速度向右爬行,那么2分钟前蜗牛在什么位置?若将时间改成3分钟前和4分钟前呢? 2分钟前(-2)+(-2)=-4(+ 2) ×(- 2)=-43分钟前(-2)+(-2) +(-2) =-6(+ 2) ×(- 3) =-64分钟前(-2)+(-2) +(-2) +(-2) =-8(+ 2) ×(- 4) =-8o如果规定:方向向右为正, 向左为负; 时间现在后为正, 现在前为负.问题4:如果蜗牛一直以每分钟2cm 的速度向左爬行,那么2分钟前蜗牛在什么位置?若将时间改成3分钟前和4分钟前呢? 2分钟前(+ 2)+(+ 2)= + 4(-2) ×(- 2)= + 43分钟前(+ 2)+(+ 2) +(+ 2) = + 6(-2) ×(- 3) = + 64分钟前(+ 2)+(+ 2) +(+ 2) +(+ 2) = + 8(-2) ×(- 4) = + 8o如果规定:方向向右为正, 向左为负; 时间现在后为正, 现在前为负.根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数;负数乘负数积为__数;
负数乘正数积为__数;正数乘负数积为__数;
乘积的绝对值等于各因数绝对值的__。正正负负乘积(同号得正)(异号得负)(+2) ×(+ 2)=+4
(+2) ×(+ 3) =+6
(+2) ×(+ 4) = +8(-2) ×(+2)=-4
(-2) ×(+3) =-6
(-2) ×(+4) =-8(+ 2) ×(- 2)=-4
(+ 2) ×(- 3) =-6
(+ 2) ×(- 4) =-8(-2) ×(- 2)= + 4
(-2) ×(- 3) = + 6
(-2) ×(- 4) =+ 8观察这四组式子思考??思考:当一个因数为0时,积是多少?如 0×3= (-2)×0=00两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。有理数乘法(multiplication)法则结合法则,观察下面两个式子:
(1) (-5)×(-2) = + (5×2) = +10;
(2) (-5) × 2 = - (5×2) = -10
从中你发现有理数乘法运算与小学乘法运算有什么联系吗?同号两数相乘得正并把绝对值相乘异号两数相乘得负并把绝对值相乘例1: 计算
(1) (-3)×9 (2) (- ) ×(-2)
=-54=-24=+6=0想一想,从计算结果中,你发现有何规律?倒数的概念:
有理数中仍然有:乘积是1的两个数互为倒数. 数a(a≠0)的倒数是什么?用式子表示:如果ab=1,则a、b互为倒数;反之,如果a、b互为倒数,则ab=1怎么求一个数的倒数?注意:求倒数与符号无关,不能改变符号。练习2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是__.
⑶如果两数互为相反数(0除外),
那么它们的倒数也是互为相反数吗?=1= -1=3= -3没有是例2 用正负数表示气温的变化量,上升为正,下降为负。
登山队攀登一座山峰,每登高1千米,气温的变化量为 -6℃,攀登3千米后,气温有什么变化?解: - 6 ×3
= -(6×3)
= -18答:气温下降18℃。一题多变,越变越聪明已知|x|=2, |y|=3,且x y<0,求x 、y的值?开放性试题1.当 a、b是什么有理数时,等式|ab|=-ab成立。解:(1)当a>0, b<0时, 等式|ab|=-ab;
(2) 当a<0, b>0时, 等式|ab|=-ab;
(3) 当a、b两数中至少有一个数为0时,等式 |ab|=-ab;变式:当 a、b是什么有理数时,等式ab= |ab|成立。解:(1)当a>0, b>0时, 等式ab =|ab|
(2) 当a<0, b<0时, 等式ab =|ab|
(3) 当a、b两数中至少有一个数为0时,等式|ab|=-ab;课堂小结通过本节课的学习,大家学会了什么?有理数的乘法法则
有理数乘法运算的方法与技巧
有理数中仍然有:乘积是1的两个数互为倒数做一做1.书面作业:课本47页习题1.2.3.
2.预习作业:预习课本37页至43页.
并想一想:
(1) 三个或三个以上不等于零的有理数相乘时,积的符号如何决定?
(2)在有理数运算中,乘法的交换律,结合律以及分配律还成立吗?谢谢大家!
1.经历探索有理数乘法法则的过程,发展观察、归纳、
猜测、验证等能力。
2.能运用法则进行简单的有理数乘法运算。
3.培养学生的语言表达能力,通过合作学习,调动学
生学习的积极性,增强 学习数学的自信心
重点: 会利用法则进行简单的有理数乘法运算。
难点: 法则的推导。
我们在小学已经熟悉正数和0的运算,
例如:
那么引入负数之后,怎样进行有理数的乘法运算呢? 比如 (-2) ×(+3) =?
(-5) ×(- 4) =?
…情境:如下图,一只蜗牛沿着直线L爬行,它现在的位置恰好在 L上的OL问题1:如果蜗牛一直以每分钟2cm 的速度向右爬行,那么2分钟后蜗牛在什么位置?若将时间改成3分钟后和4分钟后呢? o2分钟后蜗牛应在o点的右边4cm处。3分钟后蜗牛应在o点的右边6cm处。4分钟后蜗牛应在o点的右边8cm处。2+2=42 ×2=42+2+2=42 ×3=62+2+2+2=82 ×4=8如果规定:方向向右为正, 向左为负;
时间现在后为正, 现在前为负.问题1:如果蜗牛一直以每分钟2cm 的速度向右爬行,那么2分钟后蜗牛在什么位置?若将时间改成3分钟后和4分钟后呢? o2分钟后(+2)+(+2)=+4(+2) ×(+2)=+43分钟后(+2)+(+2) +(+2) =+6(+2) ×(+3) =+64分钟后(+2)+(+2) +(+2) +(+2) =+8(+2) ×(+4) = +8如果规定:方向向右为正, 向左为负;
时间现在后为正, 现在前为负.问题2:如果蜗牛一直以每分钟2cm 的速度向左爬行,那么2分钟后蜗牛在什么位置?若将时间改成3分钟后和4分钟后呢? o2分钟后(-2)+(-2)=-4(-2) ×(+2)=-43分钟后(-2)+(-2) +(-2) =-6(-2) ×(+3) =-64分钟后(-2)+(-2) +(-2) +(-2) =-8(-2) ×(+4) =-8如果规定:方向向右为正, 向左为负; 时间现在后为正, 现在前为负.问题3:如果蜗牛一直以每分钟2cm 的速度向右爬行,那么2分钟前蜗牛在什么位置?若将时间改成3分钟前和4分钟前呢? 2分钟前(-2)+(-2)=-4(+ 2) ×(- 2)=-43分钟前(-2)+(-2) +(-2) =-6(+ 2) ×(- 3) =-64分钟前(-2)+(-2) +(-2) +(-2) =-8(+ 2) ×(- 4) =-8o如果规定:方向向右为正, 向左为负; 时间现在后为正, 现在前为负.问题4:如果蜗牛一直以每分钟2cm 的速度向左爬行,那么2分钟前蜗牛在什么位置?若将时间改成3分钟前和4分钟前呢? 2分钟前(+ 2)+(+ 2)= + 4(-2) ×(- 2)= + 43分钟前(+ 2)+(+ 2) +(+ 2) = + 6(-2) ×(- 3) = + 64分钟前(+ 2)+(+ 2) +(+ 2) +(+ 2) = + 8(-2) ×(- 4) = + 8o如果规定:方向向右为正, 向左为负; 时间现在后为正, 现在前为负.根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数;负数乘负数积为__数;
负数乘正数积为__数;正数乘负数积为__数;
乘积的绝对值等于各因数绝对值的__。正正负负乘积(同号得正)(异号得负)(+2) ×(+ 2)=+4
(+2) ×(+ 3) =+6
(+2) ×(+ 4) = +8(-2) ×(+2)=-4
(-2) ×(+3) =-6
(-2) ×(+4) =-8(+ 2) ×(- 2)=-4
(+ 2) ×(- 3) =-6
(+ 2) ×(- 4) =-8(-2) ×(- 2)= + 4
(-2) ×(- 3) = + 6
(-2) ×(- 4) =+ 8观察这四组式子思考??思考:当一个因数为0时,积是多少?如 0×3= (-2)×0=00两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。有理数乘法(multiplication)法则结合法则,观察下面两个式子:
(1) (-5)×(-2) = + (5×2) = +10;
(2) (-5) × 2 = - (5×2) = -10
从中你发现有理数乘法运算与小学乘法运算有什么联系吗?同号两数相乘得正并把绝对值相乘异号两数相乘得负并把绝对值相乘例1: 计算
(1) (-3)×9 (2) (- ) ×(-2)
=-54=-24=+6=0想一想,从计算结果中,你发现有何规律?倒数的概念:
有理数中仍然有:乘积是1的两个数互为倒数. 数a(a≠0)的倒数是什么?用式子表示:如果ab=1,则a、b互为倒数;反之,如果a、b互为倒数,则ab=1怎么求一个数的倒数?注意:求倒数与符号无关,不能改变符号。练习2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是__.
⑶如果两数互为相反数(0除外),
那么它们的倒数也是互为相反数吗?=1= -1=3= -3没有是例2 用正负数表示气温的变化量,上升为正,下降为负。
登山队攀登一座山峰,每登高1千米,气温的变化量为 -6℃,攀登3千米后,气温有什么变化?解: - 6 ×3
= -(6×3)
= -18答:气温下降18℃。一题多变,越变越聪明已知|x|=2, |y|=3,且x y<0,求x 、y的值?开放性试题1.当 a、b是什么有理数时,等式|ab|=-ab成立。解:(1)当a>0, b<0时, 等式|ab|=-ab;
(2) 当a<0, b>0时, 等式|ab|=-ab;
(3) 当a、b两数中至少有一个数为0时,等式 |ab|=-ab;变式:当 a、b是什么有理数时,等式ab= |ab|成立。解:(1)当a>0, b>0时, 等式ab =|ab|
(2) 当a<0, b<0时, 等式ab =|ab|
(3) 当a、b两数中至少有一个数为0时,等式|ab|=-ab;课堂小结通过本节课的学习,大家学会了什么?有理数的乘法法则
有理数乘法运算的方法与技巧
有理数中仍然有:乘积是1的两个数互为倒数做一做1.书面作业:课本47页习题1.2.3.
2.预习作业:预习课本37页至43页.
并想一想:
(1) 三个或三个以上不等于零的有理数相乘时,积的符号如何决定?
(2)在有理数运算中,乘法的交换律,结合律以及分配律还成立吗?谢谢大家!
