湘教版七年级上册1.1具有相反意义的量课件(共39张PPT)
文档属性
| 名称 | 湘教版七年级上册1.1具有相反意义的量课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 986.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 15:45:19 | ||
图片预览











文档简介
(共39张PPT)
七年级·数学· 湘教版·上册
导学案课堂同步导学
第一章 有理数
1.1 具有相反意义的量
合作探究
分层作业
预习导学
单元概述 有理数是初中数学的起始章节,是后续学习初中数学的基础,本章学习的好坏直接影响后续初中数学的学习.
本章的学习可以让学生感受数学知识和方法的联系性,是小学数学的延续,也是之后代数运算学习的基础,充分体现了数学知识的发生发展过程
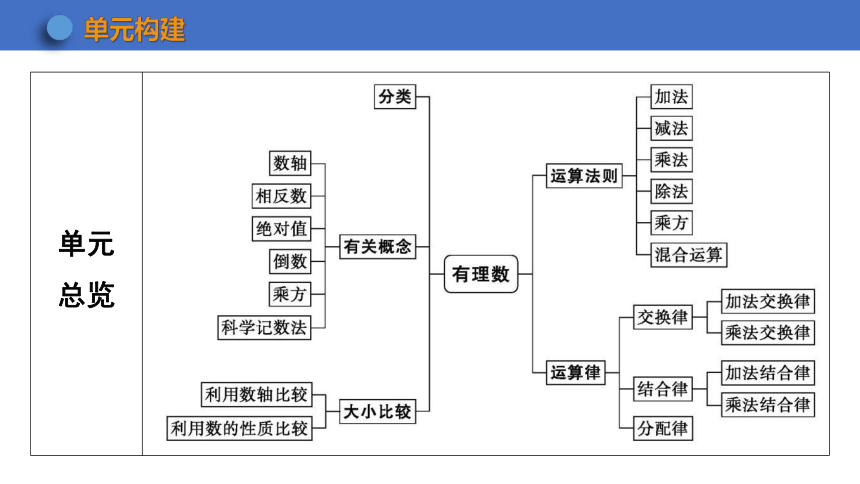
单元 总览
1.理解具有相反意义的量的概念,并能够用正、负数来表示.
2.理解有理数的概念,并能够对有理数进行正确分类.
◎重点:有理数的概念及其分类.
◎难点:理解负数、非负数等概念以及把有理数按不同标准分类.
我们今天这节数学课先来做一道语文题,请说出下面这些词语的反义词:上升、盈利、前进.(学生回答)顾名思义,反义词就是具有相反意义的词.数学主要研究对象之一就是数量,请看以下数量:上升3米,下降2米;盈利400元,亏损300元;前进1米,后退4米,每两个量之间都具有相反意义,我们称为具有相反意义的量,这就是我们本节课的主要研究内容.
用正数、负数表示具有相反意义的量
认真阅读课本本课时“议一议”之前的内容,解答下面的问题.
1.仿照“观察”中表示数的方法,请表示以下的数据.
零下2摄氏度: -2 ℃ ,零上8摄氏度: 8(或+8) ℃ ;
存入1000元: +1000 ,支出300元: -300 .
-2 ℃
8(或+8)
℃
+1000
-300
2.根据正数、负数的概念,请把上题中你所表示的四个数分类.
正数: 8,+1000 ;负数: -2,-300 .
揭示概念:在具有相反意义的一对量中,把其中一种量用正数表示,另一种量就用 负 数表示,负数是在正数前面加“ - ”,读做 负 .正数和0统称为 非负 数.
温馨提示 0既不是正数,也不是负数;“+”号可以省略不写.
8,+1000
-2,-300
负
-
负
非负
1.下面说法正确的是 ③ (填序号).
①“黑色”和“白色”表示具有相反意义的量;
②“快”和“慢”表示具有相反意义的量;
③“向南100米”和“向北1000米”表示具有相反意义的量.
③
2.如果向右走5步记为+5,那么向左走3步记为 -3 .
3.某水文观测站的记录员将高于平均水位2 m的水位记为+2 m,那么-0.5 m表示 低于平均水位0.5 m的水位 .
4.仿照“动脑筋”中的例子,自己试着举几组具有相反意义的量并表示出来.
解:略.
-3
低于平均水位0.5 m的水位
·导学建议·
在用正、负数表示具有相反意义的量时,注意追问学生每个问题情境中“+”号和“-”号的意义,如“预习自测”第3题中“-0.5 m”中的负号表示“低于平均水位”,便于学生从根本上认识正、负号和正、负数.
有理数及其分类
1.认真阅读课本本课时“议一议”,理解数的类型,并解决下面的问题.
(1) 根据你的理解,说一说-5是什么数?
解:-5是负数、整数、负整数、有理数.
·导学建议·
学生刚刚接触有理数,理解不深刻,所以在回答本题时可能只能说出其中的一种或几种,老师要细心观察学生对数的类型的理解程度,及时进行提示,特别是负整数的含义:既是负数,又是整数.
(2) 根据有理数的定义,请把下面有理数的分类补充完整.
有理数
正
0
正
负
负
归纳总结 正整数、零、负整数统称为 整 数;正分数和负分数统称为 分 数;整数和分数统称为 有理 数.
整
分
有理
·导学建议·
这种分类方法是按有理数的定义分类,请学生展示时,要强调分类的标准,并强调事物分类的时候应该遵循的原则:标准明确、不重不漏.在展示过程中强化“整数”、“分数”、“有理数”的概念,特别是“整数”的概念,学生极易丢掉0.
(3)观察课本中有理数分类的示意图,你认为有理数还可以分为哪几类?仿照上题试着写一写.
正分数和正整数可以统称为正数,那么负整数和负分数可以统称为什么数呢?0呢?从这个角度看,有理数可以分为哪几类呢?
解:负整数和负分数可以统称为负数,0既不是正数也不是负数.有理数分类如下所示:
有理数
·导学建议·
引导学生区分两个分类的标准,第一种是按定义分类,第二种是按数的性质分类,可以通俗地称为“两分法”和“三分法”.再次强调分类时必须做到不重不漏,特别注意有理数中的“0”.
2.把下列各数填在相应的大括号里:
1,-,8.9,-7,,-3.2,+1008,-0.06,28,-9,0.
负整数集合:{ -7,-9 };
整数集合:{ 1,-7,+1008,28,-9,0 };
负分数集合:{ -,-3.2,-0.06 };
-7,-9
1,-7,+1008,28,-9,0
-,-3.2,-0.06
非负数集合:{ 1,8.9,,+1 008,28,0 }.
1,8.9,,+1 008,28,0
温馨提示 因为分数与有限小数或无限循环小数之间可以相互转化,所以小数和分数统称为分数.
正、负数的意义
3.某方便面厂生产的100 g袋装方便面外包装上印有(100±5)g的字样.请问:“±5 g”表示什么意义?
解:“±5 g”表示这种方便面每袋最多比标准质量多5 g,最少比标准质量少5 g,即这种方便面一袋的质量在95 g—105 g之间.
变式训练 若某同学购买一袋这样的方便面,称了一下发现只有97 g,问该厂家在重量上有无欺诈行为?说明理由.
解:该厂无欺诈行为.因为95<97<105,所以无欺诈行为.
·导学建议·
“+”和“-”既是运算符号,又是决定数的性质的符号,当它们是性质符号时,一般表示一定的意义.例如:本题中“+”表示高于标准质量,而“-”表示低于标准质量.在教学中一定要引导学生理解每一道题目当中正、负号的意义,只有做到这一点,才能从性质和值两个角度去理解有理数.
0的意义
4.某品牌薯片每包的标准质量为50 g,超出标准质量记为正,不足记为负.则52 g可以记为 +2g ,47 g可以记为 -3g ,50 g可以记为 0g .
+2g
-3g
0g
方法归纳交流 “0”是表示“没有”吗?举例说明.
解:不是,0不再只表示“没有”.例如0 ℃表示一个温度,海拔0 m表示海平面的高度等等.
1下列选项中具有相反意义的量的是 ( D )
A.气温上升5 ℃和零下5 ℃
B.走了100米和跑了100米
C.盈利200元和支出300元
D.顺时针4圈和逆时针3圈
D
2某校七年级一班在《第一章 有理数》的测试中班级成绩的平均分为83,班主任规定:个人成绩超出平均分的部分记为“+”,低于平均分的部分记为“-”,阳阳考了80分,他应该记做 -3 .
3如果收入100元记做+100元,那么-80元表示 支出80元 .
4有四个数-3,0,1,2,其中负数有 -3 .
5用正数和负数表示下列具有相反意义的量.
-3
支出80元
-3
(1)顺时针转3圈和逆时针转2圈;
(2)粮食增产500 t和粮食减产100 t;
(3)水面上升0.2 m和水面下降0.1 m.
解:(1)若规定顺时针旋转为正,则逆时针旋转为负,两个量可以表示为+3或3,-2;
(2)若规定增产为正,则减产为负,两个量可以表示为+500或500,-100;
(3)若规定水面上升为正,则水面下降为负,两个量可以表示为+0.2或0.2,-0.1.
6仔细思考以下各对量:(1)气温降低4 ℃与气温为10 ℃;(2)胜2局与负3局;(3)转盘逆时针转3圈与顺时针转5圈;(4)收入3万元与亏损3万元.其中具有相反意义的量的有 ( C )
A.0对 B.1对 C.2对 D.3对
C
7在一次数学测验中,小明所在班级的平均分为86分,把高出平均分的部分记为正数,小明考了98分记作+12分,若小强成绩记作-4分,则他的考试分数为 ( D )
A.90分 B.88分 C.84分 D.82分
D
8下列说法正确的是 ( B )
A.一个有理数不是正数就是负数
B.一个有理数不是分数就是整数
C.有理数是指整数、分数、正有理数、零、负有理数
D.以上说法都正确
9小明的妈妈在超市买了一瓶消毒液,发现在瓶上印有这样一段文字:“净含量(750±5)mL”,这瓶消毒液至少有
745 mL.
B
745
10写出五个数(不能重复),同时满足下列三个条件:
(1)其中三个数是非正数;
(2)其中三个数是非负数;
(3)五个数都是有理数.
这五个数是 0,1,2,-1,-2(答案不唯一) .
0,1,2,-1,-2(答案不唯一)
11如图,一只甲虫在5×5的方格(每小格边长为1个单位长度)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C可以记为( +3 , +4 ),B→C可以记为( +2 , 0 ).
+3
+4
+2
0
(2)D→ A 可以记为(-4,-2).
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程长度为 10 .
(4)若这只甲虫从A处去甲虫P处的行走路线依次为(+1,+3),(+3,-2),(-2,+1),请在图中标出P的位置.
A
10
解:如图所示.
END
感谢观看 下节课再会
七年级·数学· 湘教版·上册
导学案课堂同步导学
第一章 有理数
1.1 具有相反意义的量
合作探究
分层作业
预习导学
单元概述 有理数是初中数学的起始章节,是后续学习初中数学的基础,本章学习的好坏直接影响后续初中数学的学习.
本章的学习可以让学生感受数学知识和方法的联系性,是小学数学的延续,也是之后代数运算学习的基础,充分体现了数学知识的发生发展过程
单元 总览
1.理解具有相反意义的量的概念,并能够用正、负数来表示.
2.理解有理数的概念,并能够对有理数进行正确分类.
◎重点:有理数的概念及其分类.
◎难点:理解负数、非负数等概念以及把有理数按不同标准分类.
我们今天这节数学课先来做一道语文题,请说出下面这些词语的反义词:上升、盈利、前进.(学生回答)顾名思义,反义词就是具有相反意义的词.数学主要研究对象之一就是数量,请看以下数量:上升3米,下降2米;盈利400元,亏损300元;前进1米,后退4米,每两个量之间都具有相反意义,我们称为具有相反意义的量,这就是我们本节课的主要研究内容.
用正数、负数表示具有相反意义的量
认真阅读课本本课时“议一议”之前的内容,解答下面的问题.
1.仿照“观察”中表示数的方法,请表示以下的数据.
零下2摄氏度: -2 ℃ ,零上8摄氏度: 8(或+8) ℃ ;
存入1000元: +1000 ,支出300元: -300 .
-2 ℃
8(或+8)
℃
+1000
-300
2.根据正数、负数的概念,请把上题中你所表示的四个数分类.
正数: 8,+1000 ;负数: -2,-300 .
揭示概念:在具有相反意义的一对量中,把其中一种量用正数表示,另一种量就用 负 数表示,负数是在正数前面加“ - ”,读做 负 .正数和0统称为 非负 数.
温馨提示 0既不是正数,也不是负数;“+”号可以省略不写.
8,+1000
-2,-300
负
-
负
非负
1.下面说法正确的是 ③ (填序号).
①“黑色”和“白色”表示具有相反意义的量;
②“快”和“慢”表示具有相反意义的量;
③“向南100米”和“向北1000米”表示具有相反意义的量.
③
2.如果向右走5步记为+5,那么向左走3步记为 -3 .
3.某水文观测站的记录员将高于平均水位2 m的水位记为+2 m,那么-0.5 m表示 低于平均水位0.5 m的水位 .
4.仿照“动脑筋”中的例子,自己试着举几组具有相反意义的量并表示出来.
解:略.
-3
低于平均水位0.5 m的水位
·导学建议·
在用正、负数表示具有相反意义的量时,注意追问学生每个问题情境中“+”号和“-”号的意义,如“预习自测”第3题中“-0.5 m”中的负号表示“低于平均水位”,便于学生从根本上认识正、负号和正、负数.
有理数及其分类
1.认真阅读课本本课时“议一议”,理解数的类型,并解决下面的问题.
(1) 根据你的理解,说一说-5是什么数?
解:-5是负数、整数、负整数、有理数.
·导学建议·
学生刚刚接触有理数,理解不深刻,所以在回答本题时可能只能说出其中的一种或几种,老师要细心观察学生对数的类型的理解程度,及时进行提示,特别是负整数的含义:既是负数,又是整数.
(2) 根据有理数的定义,请把下面有理数的分类补充完整.
有理数
正
0
正
负
负
归纳总结 正整数、零、负整数统称为 整 数;正分数和负分数统称为 分 数;整数和分数统称为 有理 数.
整
分
有理
·导学建议·
这种分类方法是按有理数的定义分类,请学生展示时,要强调分类的标准,并强调事物分类的时候应该遵循的原则:标准明确、不重不漏.在展示过程中强化“整数”、“分数”、“有理数”的概念,特别是“整数”的概念,学生极易丢掉0.
(3)观察课本中有理数分类的示意图,你认为有理数还可以分为哪几类?仿照上题试着写一写.
正分数和正整数可以统称为正数,那么负整数和负分数可以统称为什么数呢?0呢?从这个角度看,有理数可以分为哪几类呢?
解:负整数和负分数可以统称为负数,0既不是正数也不是负数.有理数分类如下所示:
有理数
·导学建议·
引导学生区分两个分类的标准,第一种是按定义分类,第二种是按数的性质分类,可以通俗地称为“两分法”和“三分法”.再次强调分类时必须做到不重不漏,特别注意有理数中的“0”.
2.把下列各数填在相应的大括号里:
1,-,8.9,-7,,-3.2,+1008,-0.06,28,-9,0.
负整数集合:{ -7,-9 };
整数集合:{ 1,-7,+1008,28,-9,0 };
负分数集合:{ -,-3.2,-0.06 };
-7,-9
1,-7,+1008,28,-9,0
-,-3.2,-0.06
非负数集合:{ 1,8.9,,+1 008,28,0 }.
1,8.9,,+1 008,28,0
温馨提示 因为分数与有限小数或无限循环小数之间可以相互转化,所以小数和分数统称为分数.
正、负数的意义
3.某方便面厂生产的100 g袋装方便面外包装上印有(100±5)g的字样.请问:“±5 g”表示什么意义?
解:“±5 g”表示这种方便面每袋最多比标准质量多5 g,最少比标准质量少5 g,即这种方便面一袋的质量在95 g—105 g之间.
变式训练 若某同学购买一袋这样的方便面,称了一下发现只有97 g,问该厂家在重量上有无欺诈行为?说明理由.
解:该厂无欺诈行为.因为95<97<105,所以无欺诈行为.
·导学建议·
“+”和“-”既是运算符号,又是决定数的性质的符号,当它们是性质符号时,一般表示一定的意义.例如:本题中“+”表示高于标准质量,而“-”表示低于标准质量.在教学中一定要引导学生理解每一道题目当中正、负号的意义,只有做到这一点,才能从性质和值两个角度去理解有理数.
0的意义
4.某品牌薯片每包的标准质量为50 g,超出标准质量记为正,不足记为负.则52 g可以记为 +2g ,47 g可以记为 -3g ,50 g可以记为 0g .
+2g
-3g
0g
方法归纳交流 “0”是表示“没有”吗?举例说明.
解:不是,0不再只表示“没有”.例如0 ℃表示一个温度,海拔0 m表示海平面的高度等等.
1下列选项中具有相反意义的量的是 ( D )
A.气温上升5 ℃和零下5 ℃
B.走了100米和跑了100米
C.盈利200元和支出300元
D.顺时针4圈和逆时针3圈
D
2某校七年级一班在《第一章 有理数》的测试中班级成绩的平均分为83,班主任规定:个人成绩超出平均分的部分记为“+”,低于平均分的部分记为“-”,阳阳考了80分,他应该记做 -3 .
3如果收入100元记做+100元,那么-80元表示 支出80元 .
4有四个数-3,0,1,2,其中负数有 -3 .
5用正数和负数表示下列具有相反意义的量.
-3
支出80元
-3
(1)顺时针转3圈和逆时针转2圈;
(2)粮食增产500 t和粮食减产100 t;
(3)水面上升0.2 m和水面下降0.1 m.
解:(1)若规定顺时针旋转为正,则逆时针旋转为负,两个量可以表示为+3或3,-2;
(2)若规定增产为正,则减产为负,两个量可以表示为+500或500,-100;
(3)若规定水面上升为正,则水面下降为负,两个量可以表示为+0.2或0.2,-0.1.
6仔细思考以下各对量:(1)气温降低4 ℃与气温为10 ℃;(2)胜2局与负3局;(3)转盘逆时针转3圈与顺时针转5圈;(4)收入3万元与亏损3万元.其中具有相反意义的量的有 ( C )
A.0对 B.1对 C.2对 D.3对
C
7在一次数学测验中,小明所在班级的平均分为86分,把高出平均分的部分记为正数,小明考了98分记作+12分,若小强成绩记作-4分,则他的考试分数为 ( D )
A.90分 B.88分 C.84分 D.82分
D
8下列说法正确的是 ( B )
A.一个有理数不是正数就是负数
B.一个有理数不是分数就是整数
C.有理数是指整数、分数、正有理数、零、负有理数
D.以上说法都正确
9小明的妈妈在超市买了一瓶消毒液,发现在瓶上印有这样一段文字:“净含量(750±5)mL”,这瓶消毒液至少有
745 mL.
B
745
10写出五个数(不能重复),同时满足下列三个条件:
(1)其中三个数是非正数;
(2)其中三个数是非负数;
(3)五个数都是有理数.
这五个数是 0,1,2,-1,-2(答案不唯一) .
0,1,2,-1,-2(答案不唯一)
11如图,一只甲虫在5×5的方格(每小格边长为1个单位长度)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C可以记为( +3 , +4 ),B→C可以记为( +2 , 0 ).
+3
+4
+2
0
(2)D→ A 可以记为(-4,-2).
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程长度为 10 .
(4)若这只甲虫从A处去甲虫P处的行走路线依次为(+1,+3),(+3,-2),(-2,+1),请在图中标出P的位置.
A
10
解:如图所示.
END
感谢观看 下节课再会
同课章节目录
