人教版七年级上册 2.1 整式(第2课时)课件(共33张PPT)
文档属性
| 名称 | 人教版七年级上册 2.1 整式(第2课时)课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
2.1 整 式
第二章 整式的加减
第2课时 单项式
1、某种商品每袋4.8元,在一个月内的销售量是m袋,用式子表示在这个月内销售这种商品的收入。
4.8m元
2、圆柱体的底面半径、高分别是r,h ,用式子表示圆柱体的体积。
3、有两片棉田,一片有m 公顷,平均每公顷产棉花a千克;另一片有n公顷,平均每公顷产棉花b千克,用式子表示两片棉田上棉花的总产量。
4、在一个大正方形的铁片中挖去一个小正方形铁片,大正方边长是a㎜,小正方形的边长是b ㎜,用式子表示剩余部分的面积。
π r h
(am+bn)千克
(a -b ) ㎜
一、复习回顾
用字母表示数或式子时要注意什么
1.数和字母,字母和字母相乘时,乘号可以省略不写。在省略乘号时,要把数字写在字母的前面。
2.相同字母相乘时应写成幂的形式。
3.1或-1与字母相乘时,1通常省略不写。
4.式子中出现除法运算时,要写成分数形式,带分数与字母相乘时,带分数要写成假分数的形式。
归纳:
1.抓住关键词语,明确他们的意义以及他们之间的关系,如:和、差、积、商、大、小、多、少、倍、倒数、相反数等等;
2.理清楚语句层次,明确运算顺序。
3.牢记一些概念和公式。
二、新课导入
1.边长为a的正方体的表面积为( ),体积为( )。
2.铅笔的单价是x元,圆珠笔的单价是铅笔单价的2.5倍,圆珠笔的单价是( )元。
3.一辆汽车的速度是v千米/时,它t小时行驶的路程为( )。
4.数n的相反数是( )。
5. 半径为r cm的圆的周长是 ( ) cm,面积为 ( )cm .
6a
a
2.5x
vt千米
–n
2πr
πr2
*
观察交流
6a a 2.5x vt –n 2πr πr2
你发现这些式子有什么共同特点?
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示数字与字母、字母与字母的积)。
6 a a a a a 2.5 x v t –1 n 2 π r π r r
单项式:
数与字母或字母与字母积的式子叫做单项式.单独的一个数或一个字母也是单项式.
例如:像 2017, x 等是单项式.
思考:
(1)“9”是不是单项式?“a”是不是单项式?
单独一个数或一个字母也是单项式
(2)4a b c 是不是单项式?
是单项式,单项式数字因数与字母可能一个或多个。
(3) 是不是单项式?
4a
2
不是单项式,单项式是分数形式时,分母中不含有字母。
(4) 9 + a是不是单项式?
单项式中不能含有加减运算
练习:
判断下列各代数式哪些是单项式?
x
x +1
abc b2 5ab2 y xy2 5
归纳:
判断单项式的方法
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
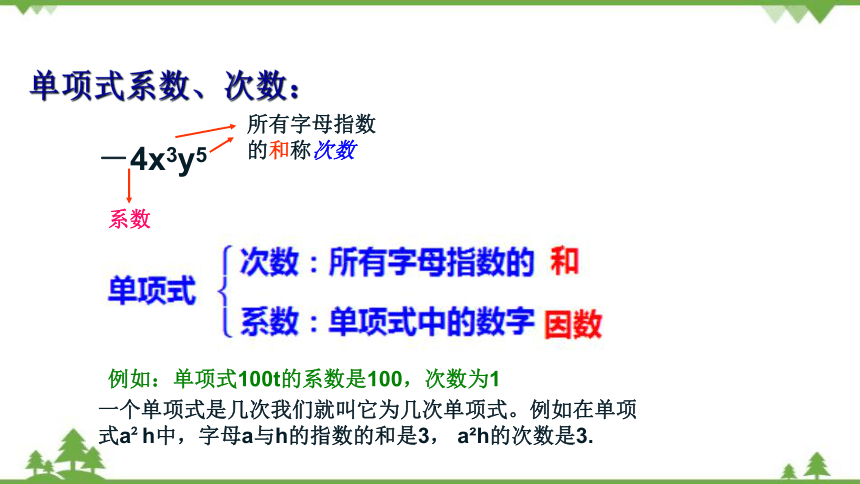
单项式系数、次数:
-4x3y5
所有字母指数的和称次数
系数
例如:单项式100t的系数是100,次数为1
一个单项式是几次我们就叫它为几次单项式。例如在单项式a h中,字母a与h的指数的和是3, a h的次数是3.
例题讲解:
例3 用单项式填空,并指出它们的系数和次数.
1. 每包书有12册,n包书有_____册;
2. 底边长为a,高为h的三角形的面积是_____;
3. 一个长方体的长和宽都是a,高为h,它的体积是_____;
4. 一台电视机原价为a元,现按原价的九折出售,这台电
视机现在的售价为____;
5. 一个长方形的长为0.9,宽为a,面积是____.
12n
系数是12,次数是1
0.9a
0.9a
系数是 1/2,次数是2
系数是 1,
次数是3
系数是0.9,次数是1
系数是0.9,次数是1
同一个式子可以表示不同的含义
思考:
(1)“-a”的系数是几?a的系数呢?
如果一个单项式中只含有字母因数,它的系数就是1或者-1。
(2)单项式π r 中,它的系数是?
圆周率π是常数,单项式中出现π时,
要将其看成系数。 (常数是指固定不变的数值)
(3)“6 ”的次数是几?
单独一个非零数的次数是0。
练习:
判断下列各单项式的系数和次数?
abc b2 5ab2 y xy2 5
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②单项式的系数包含符号,当一个单项式的系数是1或-1时,“1” 通常省略不写,当单项式的系数是带分数时,通常写成假分数;
③省略1的字母指数别漏掉;
④单项式次数只与字母指数有关,单独一个非0数字的次数是0,
00是没有意义的。
归纳:
课本练习
1.填表:
2.填空:
(1)全校学生总数是 x人 ,其中女生占总数 4 8 %,则女生人数是 ,男生人数是 ;
(2)一辆长途汽车从杨柳村出发,3小时后到达相距S千米的溪河镇,这辆长途汽车的平均速是 千米/时;
(3)产品由m千克增长10%,就达到 千克。
0.48x人
(x-0.48x)人即0.52x人
s
3
m+0.1m即(1+0.1)m
巩固应用:
1、 7 x2y的系数是7 2、 x2y2与x3没有系数
3、 ab3c2的次数是0+3+2 4、 a2的系数是 1
5、 32 x2y3的次数是7 6、 π r h系数是
1、判断下列各题是否正确
3
1
3
1
2、下列各式中单项式的个数有几个?
x2
x +y
ab
5
3
5
2x2y
a2bc 1 x2 2x
a
3
3、写出下列各单项式的系数和次数。
mx
4、若 是关于xy的单项式,且系数为 ,
次数是4,求a、b的值。
5、已知单项式16x2y4与 x2ym+2次数相同,求
m2-2m+1的值。
6、已知x2y|a|+(b+2)是关于x,y的五次单项式,
求a2-3ab的值。
课堂小结:
1.这节课我们学了什么知识?
2.你认为要注意些什么?
课堂小结
方法归纳
1.一个式子是单项式需具备两个条件:
①式子中不含运算符号“+”或“-”;
②分母中不含有字母。
2.确定单项式系数的方法:把式子中的所有字母及指数去掉。剩下的就是它的系数。
3.计算单项式的次数时要注意:
①没有写指数的字母,实际上它的指数为1,计算式不能遗漏。
②不能将系数的指数计算在内。
作业
教科书
习题2.1的第1题,第2题,第7题.
请写出一个单项式
使它的系数是2,次数是2
下列关于24的次数正确的说法是( )
A 、2 B 、4
C 、0 D 、无法确定
说出一个单项式
并且找一个同学说出它的系数和次数。
如果 5 xym-1是4次单项式,则m=
说出下列单项式的系数和次数
(1)10%m
(2)3 ×105x2y
2.1 整 式
第二章 整式的加减
第2课时 单项式
1、某种商品每袋4.8元,在一个月内的销售量是m袋,用式子表示在这个月内销售这种商品的收入。
4.8m元
2、圆柱体的底面半径、高分别是r,h ,用式子表示圆柱体的体积。
3、有两片棉田,一片有m 公顷,平均每公顷产棉花a千克;另一片有n公顷,平均每公顷产棉花b千克,用式子表示两片棉田上棉花的总产量。
4、在一个大正方形的铁片中挖去一个小正方形铁片,大正方边长是a㎜,小正方形的边长是b ㎜,用式子表示剩余部分的面积。
π r h
(am+bn)千克
(a -b ) ㎜
一、复习回顾
用字母表示数或式子时要注意什么
1.数和字母,字母和字母相乘时,乘号可以省略不写。在省略乘号时,要把数字写在字母的前面。
2.相同字母相乘时应写成幂的形式。
3.1或-1与字母相乘时,1通常省略不写。
4.式子中出现除法运算时,要写成分数形式,带分数与字母相乘时,带分数要写成假分数的形式。
归纳:
1.抓住关键词语,明确他们的意义以及他们之间的关系,如:和、差、积、商、大、小、多、少、倍、倒数、相反数等等;
2.理清楚语句层次,明确运算顺序。
3.牢记一些概念和公式。
二、新课导入
1.边长为a的正方体的表面积为( ),体积为( )。
2.铅笔的单价是x元,圆珠笔的单价是铅笔单价的2.5倍,圆珠笔的单价是( )元。
3.一辆汽车的速度是v千米/时,它t小时行驶的路程为( )。
4.数n的相反数是( )。
5. 半径为r cm的圆的周长是 ( ) cm,面积为 ( )cm .
6a
a
2.5x
vt千米
–n
2πr
πr2
*
观察交流
6a a 2.5x vt –n 2πr πr2
你发现这些式子有什么共同特点?
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示数字与字母、字母与字母的积)。
6 a a a a a 2.5 x v t –1 n 2 π r π r r
单项式:
数与字母或字母与字母积的式子叫做单项式.单独的一个数或一个字母也是单项式.
例如:像 2017, x 等是单项式.
思考:
(1)“9”是不是单项式?“a”是不是单项式?
单独一个数或一个字母也是单项式
(2)4a b c 是不是单项式?
是单项式,单项式数字因数与字母可能一个或多个。
(3) 是不是单项式?
4a
2
不是单项式,单项式是分数形式时,分母中不含有字母。
(4) 9 + a是不是单项式?
单项式中不能含有加减运算
练习:
判断下列各代数式哪些是单项式?
x
x +1
abc b2 5ab2 y xy2 5
归纳:
判断单项式的方法
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
单项式系数、次数:
-4x3y5
所有字母指数的和称次数
系数
例如:单项式100t的系数是100,次数为1
一个单项式是几次我们就叫它为几次单项式。例如在单项式a h中,字母a与h的指数的和是3, a h的次数是3.
例题讲解:
例3 用单项式填空,并指出它们的系数和次数.
1. 每包书有12册,n包书有_____册;
2. 底边长为a,高为h的三角形的面积是_____;
3. 一个长方体的长和宽都是a,高为h,它的体积是_____;
4. 一台电视机原价为a元,现按原价的九折出售,这台电
视机现在的售价为____;
5. 一个长方形的长为0.9,宽为a,面积是____.
12n
系数是12,次数是1
0.9a
0.9a
系数是 1/2,次数是2
系数是 1,
次数是3
系数是0.9,次数是1
系数是0.9,次数是1
同一个式子可以表示不同的含义
思考:
(1)“-a”的系数是几?a的系数呢?
如果一个单项式中只含有字母因数,它的系数就是1或者-1。
(2)单项式π r 中,它的系数是?
圆周率π是常数,单项式中出现π时,
要将其看成系数。 (常数是指固定不变的数值)
(3)“6 ”的次数是几?
单独一个非零数的次数是0。
练习:
判断下列各单项式的系数和次数?
abc b2 5ab2 y xy2 5
确定单项式的系数及次数时,应注意:
①圆周率π是常数;
②单项式的系数包含符号,当一个单项式的系数是1或-1时,“1” 通常省略不写,当单项式的系数是带分数时,通常写成假分数;
③省略1的字母指数别漏掉;
④单项式次数只与字母指数有关,单独一个非0数字的次数是0,
00是没有意义的。
归纳:
课本练习
1.填表:
2.填空:
(1)全校学生总数是 x人 ,其中女生占总数 4 8 %,则女生人数是 ,男生人数是 ;
(2)一辆长途汽车从杨柳村出发,3小时后到达相距S千米的溪河镇,这辆长途汽车的平均速是 千米/时;
(3)产品由m千克增长10%,就达到 千克。
0.48x人
(x-0.48x)人即0.52x人
s
3
m+0.1m即(1+0.1)m
巩固应用:
1、 7 x2y的系数是7 2、 x2y2与x3没有系数
3、 ab3c2的次数是0+3+2 4、 a2的系数是 1
5、 32 x2y3的次数是7 6、 π r h系数是
1、判断下列各题是否正确
3
1
3
1
2、下列各式中单项式的个数有几个?
x2
x +y
ab
5
3
5
2x2y
a2bc 1 x2 2x
a
3
3、写出下列各单项式的系数和次数。
mx
4、若 是关于xy的单项式,且系数为 ,
次数是4,求a、b的值。
5、已知单项式16x2y4与 x2ym+2次数相同,求
m2-2m+1的值。
6、已知x2y|a|+(b+2)是关于x,y的五次单项式,
求a2-3ab的值。
课堂小结:
1.这节课我们学了什么知识?
2.你认为要注意些什么?
课堂小结
方法归纳
1.一个式子是单项式需具备两个条件:
①式子中不含运算符号“+”或“-”;
②分母中不含有字母。
2.确定单项式系数的方法:把式子中的所有字母及指数去掉。剩下的就是它的系数。
3.计算单项式的次数时要注意:
①没有写指数的字母,实际上它的指数为1,计算式不能遗漏。
②不能将系数的指数计算在内。
作业
教科书
习题2.1的第1题,第2题,第7题.
请写出一个单项式
使它的系数是2,次数是2
下列关于24的次数正确的说法是( )
A 、2 B 、4
C 、0 D 、无法确定
说出一个单项式
并且找一个同学说出它的系数和次数。
如果 5 xym-1是4次单项式,则m=
说出下列单项式的系数和次数
(1)10%m
(2)3 ×105x2y
