2.15 用计算器进行计算 课件(共23张PPT)
文档属性
| 名称 | 2.15 用计算器进行计算 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 16:19:04 | ||
图片预览








文档简介
(共23张PPT)
2.15 用计算器进行计算
华师大版 七年级上册
教学目标
【教学目标】
1.让学生学会使用计算器进行有理数加、减、乘、除、乘方运算;
2.让学生能运用计算器进行实际问题的有关运算;
3.让学生体会解决问题的程序思想,探索使用规律和技巧.
【重点】使用计算器进行有理数加、减、乘、除、乘方运算.
【难点】运用计算器进行实际问题的有关运算.
新知导入
已知一个圆柱的底面半径为2.32cm,高为7.06cm,求这个圆柱的体积.
我们知道,圆柱的体积=底面积×高.
因此,计算这个圆柱的体积就要做这样的计算:
π×2.322×7.06.
碰到复杂的计算,我们应该怎么办?
碰到复杂的计算,我们可以利用电子计算器(简称计算器)来完成.
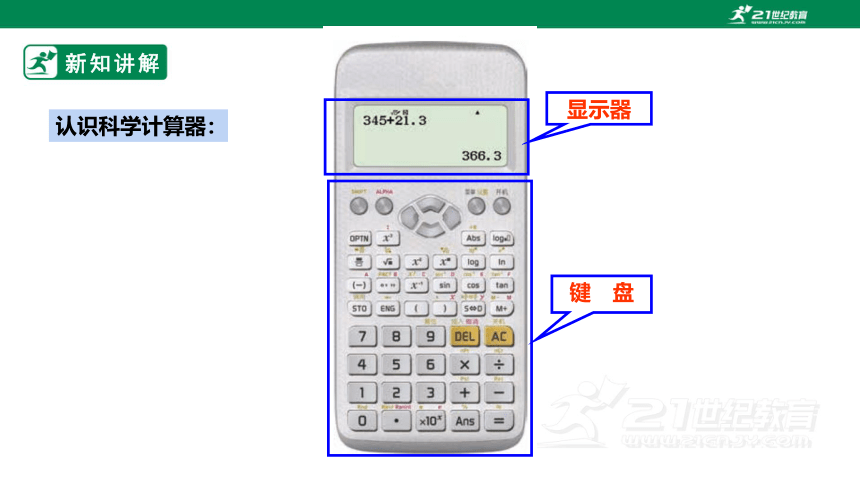
新知讲解
显示器
键 盘
认识科学计算器:
新知讲解
开启计算机键
清除键
完成运算或执行指令
运算键
执行第一功能
执行第二功能
认识科学计算器:
新知讲解
计算器一些常用键功能
开启键,清除键
第二功能键
数字键
小数点
分数键
四则运算键
完成运算或执行指令
删除键,删除光标所在位置的数字或符号
平方运算键、乘方运算键
答案存储器
0
1
2
3
5
6
7
8
4
9
ab/c
+
-
×
÷
=
DEL
ON/C
2ndf
xy
x2
新知讲解
例1 下面我们尝试运用计算器解题用计算器求345+21.3
用计算器求345 + 21.3的过程为:
键入 3 4 5 + 2 1 . 3 ,显示器显示运算式子345+21.3,
再按 = ,在第二行显示运算结果 ,
若需得到小数形式的结果,可继续按S D ,显示366. 3,
即345 + 21.3= =366. 3
在键入数据后,也可直接按 SHIFT = ,得到小数形式的结果。
做一做
按例1的方法,用计算器求105.3 - 243的值.
用计算器求105.3-243的过程为:
键入 1 0 5 . 3 - 2 4 3 ,显示器显示运算式子105.3-243,
再按 = ,在第二行显示运算结果 ,
若需得到小数形式的结果,可继续按S D ,显示-137.7,
即345 + 21.3= =-137.7
在键入数据后,也可直接按 SHIFT = ,得到小数形式的结果。
新知讲解
例2 用计算器求31.2 ÷ (-0.4).
解 用计算器求31.2 ÷(-0. 4)的按键顺序是: 3 1 . 2 ÷ (-) 0 . 4 =
显示结果为-78,所以
31.2 +(-0.4) =-78.
(1)输入0.4时,也可以省去小数点前的0,按 即可.
(2)不同型号的计算器可能会有不同的按键顺序.
如输入负数-5,有的计算器是 或 , 有的则为 .
做一做
按例2的方法,用计算器求8.2 x (-4.3)÷2.5的值
解: 用计算器求8.2 x (-4.3)÷2.5的按键顺序是:
8 . 2 x (-) 4 . 3 ÷ 2 . 5 =
显示结果为14.104,所以
8.2 x (-4.3)÷2.5=14.104
新知讲解
这是加法和乘法的混合运算对于加、减、乘、除和乘方的混合运算,只要按算式的书写顺序输人,计算器会按要求算出结果。
例3 用计算器求62.2 +4 x7.8
因此,本题的按键顺序是:
6 2 . 2 + 4 x 7 . 8 = S D
显示结果为93.4,所以
62.2 + 4 x7.8 = 93.4.
做一做
按例3的方法,用计算器求( -29.4) x2 ÷4.2÷( -7)的值
本题的按键顺序是:
( -) 2 9 . 4 x 2 ÷ 4 . 2 ÷ ( -) 7 =
显示结果为2,所以
( -29.4) x2 ÷4.2÷( -7) = 2
新知讲解
例4 用计算器求2.73
用计算器求2.73,可以使用求立方的专用键 x3 ,按键顺序是:
2 . 7 x3 = S D
显示结果为19. 683 ,所以
2.73= 19.683
新知讲解
也可以使用乘方的专用键 x口
( 按 2 . 7 x口 后,
出现2.7口) ,按键顺序是:
2 . 7 x口 3 = S D
新知讲解
用计算器求一个数的正整数次幂,不同的计算器可能会有不同的按键方式.
当求一个数的平方或立方时,不少计算器都有专用键.
课堂练习
1.计算器上用于开启计算器,使之工作的键是( )
A.ON B.CE C.OFF D.+
2.小清误将92输为693,要想将其删除掉,应按键( )
A.AC B. CE C.OFF D.DEL
3.计算器上AC键的功能是( )
A.开启计算器 B.关闭计算器
C.清除全部内容 D.清除局部内容
A
D
C
课堂练习
4.计算:
(1)(-29.4)×2÷(-7); (2)84;
(3)3.24×103+1.2×105; (4)3.12×106÷(-2.4×102).
解:(1)原式=8.4;
(2)原式=4096;
(3)原式=123240;
(4)原式=-13000.
课堂练习
5.计算:
(1)-3.73+(-3.8)4(精确到0.01);
(2)[6.38÷(-2)+6.53]×17.3(精确到百位).
解:(1)原式=157.8606≈157.86;
(2)原式=4695.8255≈4.7×103.
课堂练习
6.用计算器计算下列各式,探求你所发现的规律:
(1)12345679×9=__________________________.
(2)12345679×18=_________________________.
(3)12345679×9n(1≤n≤9的整数)=_______________.
111 111 111
222 222 222
nnn nnn nnn
解:12345679×9n(1≤n≤9的整数)所得的积为:每个数都是n的9位数.
7.用计算器计算:
一张纸的厚度大约是0.1毫米,把它对折30次后,将它的厚度与珠穆
朗玛峰的高度比较一下(珠穆朗玛峰高约8848米)看谁更高.
解此类题目时,先根据题意列出算式,再用计算器计算.
解:根据题意,得 0.1×230=107374182.4(毫米),
107374182.4毫米=107374.1824米,
所以厚度为107374.1824米,比珠穆朗玛峰还要高
课堂总结
1.怎样使用计算器进行有理数的加、减、乘、除和乘方的混合运算?
对于加、减、乘、除和乘方的混合运算,只要按算式的书写顺序输入,计算器会按要求算出结果.
2.怎样使用计算器求一个数的正整数次幂?
使用计算器求一个数的正整数次幂,可以使用乘方的专用键来进行计算.
3.使用计算器进行运算,一定要注意按键的顺序.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.15 用计算器进行计算
华师大版 七年级上册
教学目标
【教学目标】
1.让学生学会使用计算器进行有理数加、减、乘、除、乘方运算;
2.让学生能运用计算器进行实际问题的有关运算;
3.让学生体会解决问题的程序思想,探索使用规律和技巧.
【重点】使用计算器进行有理数加、减、乘、除、乘方运算.
【难点】运用计算器进行实际问题的有关运算.
新知导入
已知一个圆柱的底面半径为2.32cm,高为7.06cm,求这个圆柱的体积.
我们知道,圆柱的体积=底面积×高.
因此,计算这个圆柱的体积就要做这样的计算:
π×2.322×7.06.
碰到复杂的计算,我们应该怎么办?
碰到复杂的计算,我们可以利用电子计算器(简称计算器)来完成.
新知讲解
显示器
键 盘
认识科学计算器:
新知讲解
开启计算机键
清除键
完成运算或执行指令
运算键
执行第一功能
执行第二功能
认识科学计算器:
新知讲解
计算器一些常用键功能
开启键,清除键
第二功能键
数字键
小数点
分数键
四则运算键
完成运算或执行指令
删除键,删除光标所在位置的数字或符号
平方运算键、乘方运算键
答案存储器
0
1
2
3
5
6
7
8
4
9
ab/c
+
-
×
÷
=
DEL
ON/C
2ndf
xy
x2
新知讲解
例1 下面我们尝试运用计算器解题用计算器求345+21.3
用计算器求345 + 21.3的过程为:
键入 3 4 5 + 2 1 . 3 ,显示器显示运算式子345+21.3,
再按 = ,在第二行显示运算结果 ,
若需得到小数形式的结果,可继续按S D ,显示366. 3,
即345 + 21.3= =366. 3
在键入数据后,也可直接按 SHIFT = ,得到小数形式的结果。
做一做
按例1的方法,用计算器求105.3 - 243的值.
用计算器求105.3-243的过程为:
键入 1 0 5 . 3 - 2 4 3 ,显示器显示运算式子105.3-243,
再按 = ,在第二行显示运算结果 ,
若需得到小数形式的结果,可继续按S D ,显示-137.7,
即345 + 21.3= =-137.7
在键入数据后,也可直接按 SHIFT = ,得到小数形式的结果。
新知讲解
例2 用计算器求31.2 ÷ (-0.4).
解 用计算器求31.2 ÷(-0. 4)的按键顺序是: 3 1 . 2 ÷ (-) 0 . 4 =
显示结果为-78,所以
31.2 +(-0.4) =-78.
(1)输入0.4时,也可以省去小数点前的0,按 即可.
(2)不同型号的计算器可能会有不同的按键顺序.
如输入负数-5,有的计算器是 或 , 有的则为 .
做一做
按例2的方法,用计算器求8.2 x (-4.3)÷2.5的值
解: 用计算器求8.2 x (-4.3)÷2.5的按键顺序是:
8 . 2 x (-) 4 . 3 ÷ 2 . 5 =
显示结果为14.104,所以
8.2 x (-4.3)÷2.5=14.104
新知讲解
这是加法和乘法的混合运算对于加、减、乘、除和乘方的混合运算,只要按算式的书写顺序输人,计算器会按要求算出结果。
例3 用计算器求62.2 +4 x7.8
因此,本题的按键顺序是:
6 2 . 2 + 4 x 7 . 8 = S D
显示结果为93.4,所以
62.2 + 4 x7.8 = 93.4.
做一做
按例3的方法,用计算器求( -29.4) x2 ÷4.2÷( -7)的值
本题的按键顺序是:
( -) 2 9 . 4 x 2 ÷ 4 . 2 ÷ ( -) 7 =
显示结果为2,所以
( -29.4) x2 ÷4.2÷( -7) = 2
新知讲解
例4 用计算器求2.73
用计算器求2.73,可以使用求立方的专用键 x3 ,按键顺序是:
2 . 7 x3 = S D
显示结果为19. 683 ,所以
2.73= 19.683
新知讲解
也可以使用乘方的专用键 x口
( 按 2 . 7 x口 后,
出现2.7口) ,按键顺序是:
2 . 7 x口 3 = S D
新知讲解
用计算器求一个数的正整数次幂,不同的计算器可能会有不同的按键方式.
当求一个数的平方或立方时,不少计算器都有专用键.
课堂练习
1.计算器上用于开启计算器,使之工作的键是( )
A.ON B.CE C.OFF D.+
2.小清误将92输为693,要想将其删除掉,应按键( )
A.AC B. CE C.OFF D.DEL
3.计算器上AC键的功能是( )
A.开启计算器 B.关闭计算器
C.清除全部内容 D.清除局部内容
A
D
C
课堂练习
4.计算:
(1)(-29.4)×2÷(-7); (2)84;
(3)3.24×103+1.2×105; (4)3.12×106÷(-2.4×102).
解:(1)原式=8.4;
(2)原式=4096;
(3)原式=123240;
(4)原式=-13000.
课堂练习
5.计算:
(1)-3.73+(-3.8)4(精确到0.01);
(2)[6.38÷(-2)+6.53]×17.3(精确到百位).
解:(1)原式=157.8606≈157.86;
(2)原式=4695.8255≈4.7×103.
课堂练习
6.用计算器计算下列各式,探求你所发现的规律:
(1)12345679×9=__________________________.
(2)12345679×18=_________________________.
(3)12345679×9n(1≤n≤9的整数)=_______________.
111 111 111
222 222 222
nnn nnn nnn
解:12345679×9n(1≤n≤9的整数)所得的积为:每个数都是n的9位数.
7.用计算器计算:
一张纸的厚度大约是0.1毫米,把它对折30次后,将它的厚度与珠穆
朗玛峰的高度比较一下(珠穆朗玛峰高约8848米)看谁更高.
解此类题目时,先根据题意列出算式,再用计算器计算.
解:根据题意,得 0.1×230=107374182.4(毫米),
107374182.4毫米=107374.1824米,
所以厚度为107374.1824米,比珠穆朗玛峰还要高
课堂总结
1.怎样使用计算器进行有理数的加、减、乘、除和乘方的混合运算?
对于加、减、乘、除和乘方的混合运算,只要按算式的书写顺序输入,计算器会按要求算出结果.
2.怎样使用计算器求一个数的正整数次幂?
使用计算器求一个数的正整数次幂,可以使用乘方的专用键来进行计算.
3.使用计算器进行运算,一定要注意按键的顺序.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
