2022-2023学年度人教版数学九年级上册 24.1.2垂直于弦的直径 章节培优训练试卷(word版含答案)
文档属性
| 名称 | 2022-2023学年度人教版数学九年级上册 24.1.2垂直于弦的直径 章节培优训练试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 519.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 00:00:00 | ||
图片预览



文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
一、选择题
1.一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )
A.① B.② C.③ D.④
2. 如图,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为( )
A.8 B.12 C.16 D.2
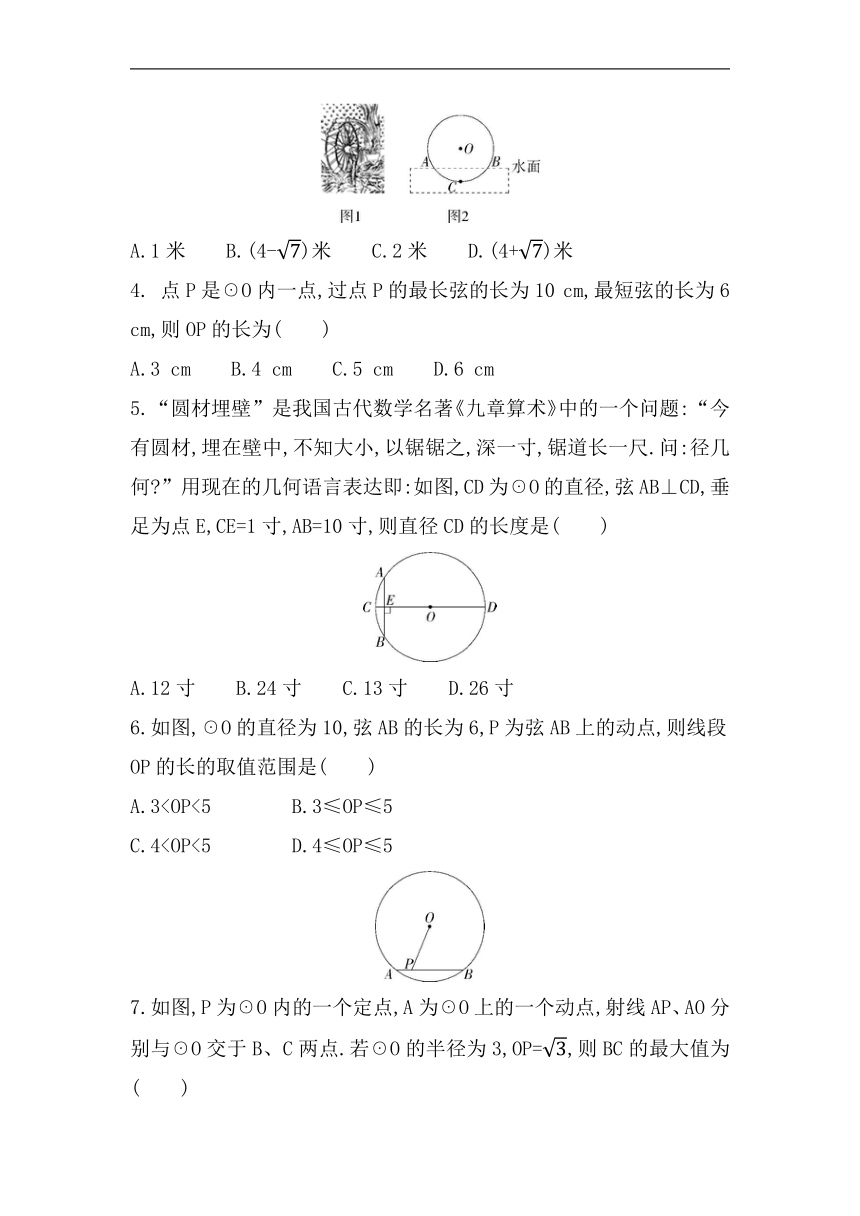
3. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且☉O被水面截得的弦AB长为6米,☉O的半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4-)米 C.2米 D.(4+)米
4. 点P是☉O内一点,过点P的最长弦的长为10 cm,最短弦的长为6 cm,则OP的长为( )
A.3 cm B.4 cm C.5 cm D.6 cm
5.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何 ”用现在的几何语言表达即:如图,CD为☉O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
6.如图,☉O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP的长的取值范围是( )
A.3C.47.如图,P为☉O内的一个定点,A为☉O上的一个动点,射线AP、AO分别与☉O交于B、C两点.若☉O的半径为3,OP=,则BC的最大值为( )
A.2 B.3 C. D.3
8.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分 B.0.8厘米/分
C.1.2厘米/分 D.1.4厘米/分
二、填空题
9.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
10.如图,在☉O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
11.如图,在半径为5的☉O中,M为弦AB的中点,连接OM,若OM=1,则AB的长为 .
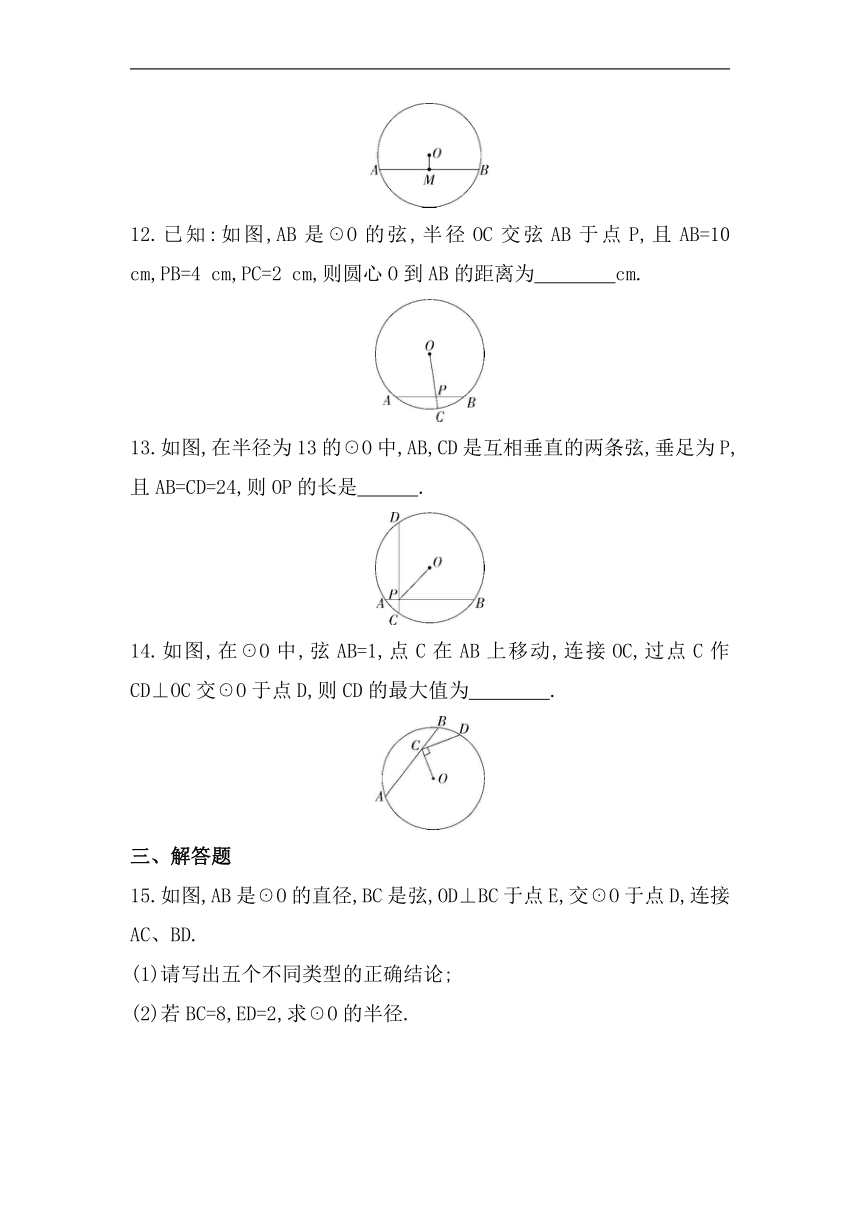
12.已知:如图,AB是☉O的弦,半径OC交弦AB于点P,且AB=10 cm,PB=4 cm,PC=2 cm,则圆心O到AB的距离为 cm.
13.如图,在半径为13的☉O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是 .
14.如图,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .
三、解答题
15.如图,AB是☉O的直径,BC是弦,OD⊥BC于点E,交☉O于点D,连接AC、BD.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求☉O的半径.
16.如图,要把残破的圆片修复完整,已知弧上的点A、B、C.
(1)试确定所在圆的圆心O;
(2)若△ABC是等腰三角形,底边BC=10厘米,腰AB=6厘米,求圆片的半径R.(结果保留根号)
答案全解全析
一、选择题
1.答案 B 第②块有一段完整的弧,可在这段弧上任取三点作两条弦,作出这两条弦的垂直平分线,它们的交点即为圆心,进而可得半径.故选B.
2.答案 C 如图,连接OA,
∵☉O的直径CD=20,OM∶OC=3∶5,
∴OC=10,OM=6.∵AB⊥CD,
∴AM===8,∴AB=2AM=16.故选C.
答案 B 如图,连接OC交AB于D,连接OA,∵点C为运行轨道的最低点,∴OC⊥AB,∴AD=AB=3(米).在Rt△OAD中,
OD===(米),
∴点C到弦AB所在直线的距离CD=OC-OD=(4-)米.故选B.
4.答案 B 如图所示,CD⊥AB于点P.根据题意,得AB=10 cm,CD=6 cm.∵AB是直径,且CD⊥AB,∴CP=CD=3 cm.根据勾股定理,得OP===4(cm).故选B.
5.答案 D 如图,连接OA,
∵AB⊥CD,且AB=10寸,∴AE=BE=5寸.设☉O的半径OA的长为x寸,则OC=OD=x寸.∵CE=1寸,∴OE=(x-1)寸.在Rt△AOE中,由勾股定理得x2-(x-1)2=52,化简得x2-x2+2x-1=25,即2x=26,∴CD=26寸,即直径CD的长为26寸.
6. 答案 D 如图,连接OA,过点O作OH⊥AB于H,则AH=HB=AB=3.
∵☉O的直径为10,
∴OA=5,由勾股定理得,OH===4,当点P与点A(或点B)重合时,OP的长度最大,当点P与点H重合时,OP的长度最小,
∴线段OP的长的取值范围是4≤OP≤5.
7. 答案 A 如图,过点O作OE⊥AB于E,
∵O为圆心,
∴AE=BE,
∵OA=OC,∴OE为△ABC的中位线,
∴OE=BC.
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合,即OP⊥AB时,BC取得最大值,∴BC的最大值为2OP=2.故选A.
8. 答案 A 设“图上”圆的圆心为O,连接OA,作OD⊥AB于D,延长DO交圆于点C,如图所示:
∵AB=16厘米,
∴AD=AB=8(厘米),
∵OA=10厘米,
∴OD===6(厘米),
∴DC=OC+OD=10+6=16(厘米),
∵太阳从所处位置到完全跳出海平面的时间为16分钟,
∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),故选A.
二、填空题
9.答案 3
解析 过点O作OH⊥CD于H,连接OC,如图,则OC=AB=5,CH=DH=CD=4,在Rt△OCH中,OH==3,所以CD与AB之间的距离是3.
10.答案 45°
解析 ∵OC⊥AB,∴AC=BC=AB=×4=2,∵OC=2,∴△AOC为等腰直角三角形,
∴∠AOC=45°.
11.答案 4
解析 如图,连接OA,∵M为AB的中点,O是圆心,
∴OM⊥AB,AM=BM,∴∠OMA=90°,由勾股定理得BM=AM===2,∴AB=AM+BM=2+2=4.
12. 答案 2
解析 如图,连接OA,作OD⊥AB于D,则AD=BD=AB=5(cm),∴DP=BD-PB=1(cm).设OA=OC=r cm,在Rt△AOD和Rt△OPD中,由勾股定理得OD2=OA2-AD2=OP2-DP2,即r2-52=(r-2)2-12,解得r=7,即OA=7 cm,∴OD==2(cm),即圆心O到AB的距离为2 cm.
13. 答案 5
解析 如图,作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
∴DN=CD,BM=AB,∵AB=CD=24,∴DN=BM=12,∴OM=ON==5.∵弦AB、CD互相垂直,∴∠DPB=90°.∵OM⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是矩形.∵OM=ON,∴四边形MONP是正方形,∴OP=5.
14.答案
解析 如图,连接OD,
∵CD⊥OC,
∴∠DCO=90°,
∴CD==(r为圆O的半径),当OC的长最小时,CD的长最大,而OC⊥AB时,OC的长最小,此时D、B两点重合,
CD=CB=AB=×1=,
∴CD的最大值为.
三、解答题
15.解析 (1)正确的结论:
CE=BE,=,OE=AC,∠C=90°,AC∥OD.(答案不唯一)
(2)∵OD⊥BC,OD过圆心O,BC=8,
∴∠OEB=90°,BE=CE=4,
设☉O的半径为R,则OB=OD=R,
由勾股定理得OB2=OE2+BE2,
即R2=(R-2)2+42,
解得R=5,
即☉O的半径是5.
16.解析 (1)如图,作AB,AC的垂直平分线交于点O,点O即为所在圆的圆心.
(2)如图,连接OA,OB,OC,OA交BC于点D,因为BA=AC,OB=OC,所以AO是BC的垂直平分线,即AO⊥BC,CD=BC,
所以CD=×10=5厘米,所以AD==厘米.
根据勾股定理得(R-)2+52=R2,解得R=厘米.
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
一、选择题
1.一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )
A.① B.② C.③ D.④
2. 如图,☉O的直径CD=20,AB是☉O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为( )
A.8 B.12 C.16 D.2
3. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且☉O被水面截得的弦AB长为6米,☉O的半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4-)米 C.2米 D.(4+)米
4. 点P是☉O内一点,过点P的最长弦的长为10 cm,最短弦的长为6 cm,则OP的长为( )
A.3 cm B.4 cm C.5 cm D.6 cm
5.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何 ”用现在的几何语言表达即:如图,CD为☉O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是( )
A.12寸 B.24寸 C.13寸 D.26寸
6.如图,☉O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP的长的取值范围是( )
A.3
A.2 B.3 C. D.3
8.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )
A.1.0厘米/分 B.0.8厘米/分
C.1.2厘米/分 D.1.4厘米/分
二、填空题
9.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .
10.如图,在☉O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
11.如图,在半径为5的☉O中,M为弦AB的中点,连接OM,若OM=1,则AB的长为 .
12.已知:如图,AB是☉O的弦,半径OC交弦AB于点P,且AB=10 cm,PB=4 cm,PC=2 cm,则圆心O到AB的距离为 cm.
13.如图,在半径为13的☉O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是 .
14.如图,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .
三、解答题
15.如图,AB是☉O的直径,BC是弦,OD⊥BC于点E,交☉O于点D,连接AC、BD.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求☉O的半径.
16.如图,要把残破的圆片修复完整,已知弧上的点A、B、C.
(1)试确定所在圆的圆心O;
(2)若△ABC是等腰三角形,底边BC=10厘米,腰AB=6厘米,求圆片的半径R.(结果保留根号)
答案全解全析
一、选择题
1.答案 B 第②块有一段完整的弧,可在这段弧上任取三点作两条弦,作出这两条弦的垂直平分线,它们的交点即为圆心,进而可得半径.故选B.
2.答案 C 如图,连接OA,
∵☉O的直径CD=20,OM∶OC=3∶5,
∴OC=10,OM=6.∵AB⊥CD,
∴AM===8,∴AB=2AM=16.故选C.
答案 B 如图,连接OC交AB于D,连接OA,∵点C为运行轨道的最低点,∴OC⊥AB,∴AD=AB=3(米).在Rt△OAD中,
OD===(米),
∴点C到弦AB所在直线的距离CD=OC-OD=(4-)米.故选B.
4.答案 B 如图所示,CD⊥AB于点P.根据题意,得AB=10 cm,CD=6 cm.∵AB是直径,且CD⊥AB,∴CP=CD=3 cm.根据勾股定理,得OP===4(cm).故选B.
5.答案 D 如图,连接OA,
∵AB⊥CD,且AB=10寸,∴AE=BE=5寸.设☉O的半径OA的长为x寸,则OC=OD=x寸.∵CE=1寸,∴OE=(x-1)寸.在Rt△AOE中,由勾股定理得x2-(x-1)2=52,化简得x2-x2+2x-1=25,即2x=26,∴CD=26寸,即直径CD的长为26寸.
6. 答案 D 如图,连接OA,过点O作OH⊥AB于H,则AH=HB=AB=3.
∵☉O的直径为10,
∴OA=5,由勾股定理得,OH===4,当点P与点A(或点B)重合时,OP的长度最大,当点P与点H重合时,OP的长度最小,
∴线段OP的长的取值范围是4≤OP≤5.
7. 答案 A 如图,过点O作OE⊥AB于E,
∵O为圆心,
∴AE=BE,
∵OA=OC,∴OE为△ABC的中位线,
∴OE=BC.
∵OE≤OP,
∴BC≤2OP,
∴当E、P重合,即OP⊥AB时,BC取得最大值,∴BC的最大值为2OP=2.故选A.
8. 答案 A 设“图上”圆的圆心为O,连接OA,作OD⊥AB于D,延长DO交圆于点C,如图所示:
∵AB=16厘米,
∴AD=AB=8(厘米),
∵OA=10厘米,
∴OD===6(厘米),
∴DC=OC+OD=10+6=16(厘米),
∵太阳从所处位置到完全跳出海平面的时间为16分钟,
∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),故选A.
二、填空题
9.答案 3
解析 过点O作OH⊥CD于H,连接OC,如图,则OC=AB=5,CH=DH=CD=4,在Rt△OCH中,OH==3,所以CD与AB之间的距离是3.
10.答案 45°
解析 ∵OC⊥AB,∴AC=BC=AB=×4=2,∵OC=2,∴△AOC为等腰直角三角形,
∴∠AOC=45°.
11.答案 4
解析 如图,连接OA,∵M为AB的中点,O是圆心,
∴OM⊥AB,AM=BM,∴∠OMA=90°,由勾股定理得BM=AM===2,∴AB=AM+BM=2+2=4.
12. 答案 2
解析 如图,连接OA,作OD⊥AB于D,则AD=BD=AB=5(cm),∴DP=BD-PB=1(cm).设OA=OC=r cm,在Rt△AOD和Rt△OPD中,由勾股定理得OD2=OA2-AD2=OP2-DP2,即r2-52=(r-2)2-12,解得r=7,即OA=7 cm,∴OD==2(cm),即圆心O到AB的距离为2 cm.
13. 答案 5
解析 如图,作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
∴DN=CD,BM=AB,∵AB=CD=24,∴DN=BM=12,∴OM=ON==5.∵弦AB、CD互相垂直,∴∠DPB=90°.∵OM⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是矩形.∵OM=ON,∴四边形MONP是正方形,∴OP=5.
14.答案
解析 如图,连接OD,
∵CD⊥OC,
∴∠DCO=90°,
∴CD==(r为圆O的半径),当OC的长最小时,CD的长最大,而OC⊥AB时,OC的长最小,此时D、B两点重合,
CD=CB=AB=×1=,
∴CD的最大值为.
三、解答题
15.解析 (1)正确的结论:
CE=BE,=,OE=AC,∠C=90°,AC∥OD.(答案不唯一)
(2)∵OD⊥BC,OD过圆心O,BC=8,
∴∠OEB=90°,BE=CE=4,
设☉O的半径为R,则OB=OD=R,
由勾股定理得OB2=OE2+BE2,
即R2=(R-2)2+42,
解得R=5,
即☉O的半径是5.
16.解析 (1)如图,作AB,AC的垂直平分线交于点O,点O即为所在圆的圆心.
(2)如图,连接OA,OB,OC,OA交BC于点D,因为BA=AC,OB=OC,所以AO是BC的垂直平分线,即AO⊥BC,CD=BC,
所以CD=×10=5厘米,所以AD==厘米.
根据勾股定理得(R-)2+52=R2,解得R=厘米.
同课章节目录
