2022-2023学年 人教版九年级数学上册22.3.3实物抛物线问题 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年 人教版九年级数学上册22.3.3实物抛物线问题 章节培优训练试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 447.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 08:31:20 | ||
图片预览




文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十二章 二次函数
22.3 实际问题与二次函数
第3课时 实物抛物线问题
一、选择题
1. 北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线型钢拱的函数表达式为( )
A.y=x2 B.y=-x2 C.y=x2 D.y=-x2
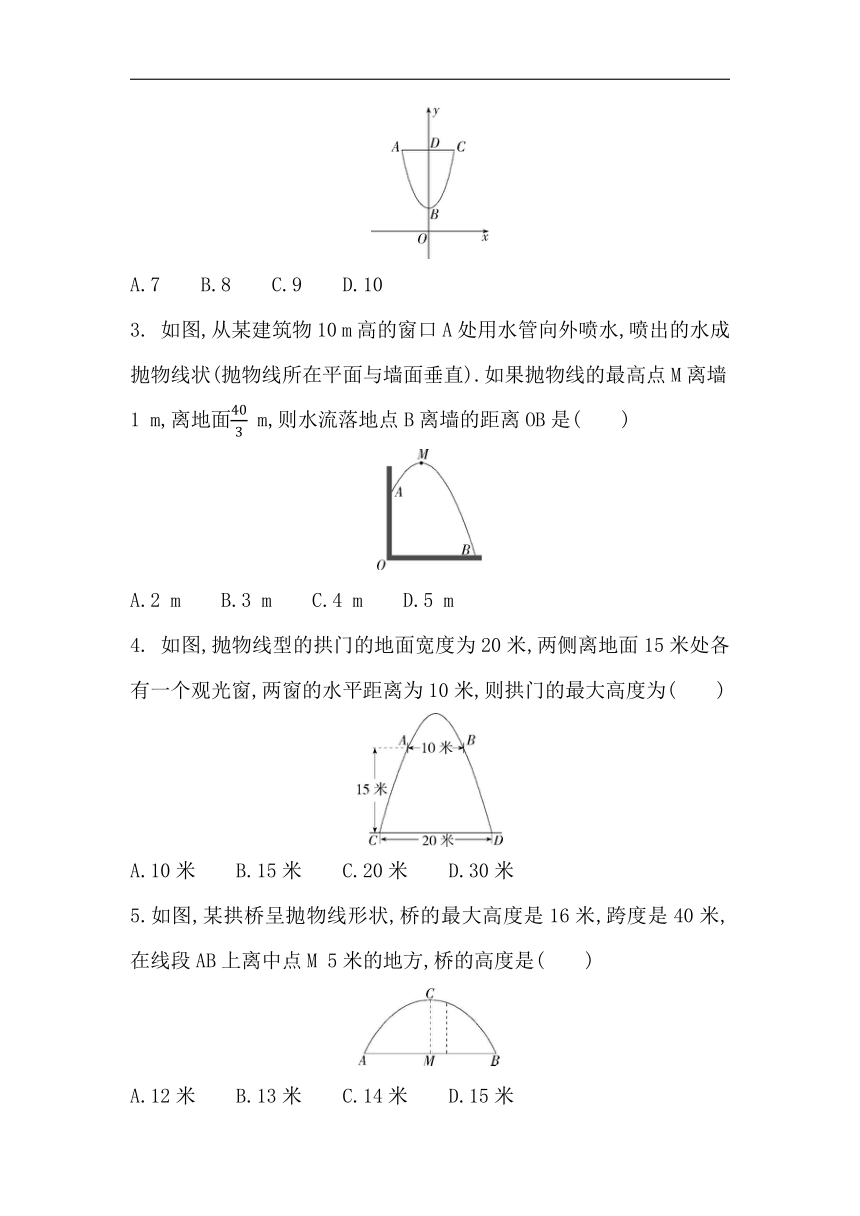
2. 如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线y=x2+5的一部分,则杯口的口径AC=( )
A.7 B.8 C.9 D.10
3. 如图,从某建筑物10 m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1 m,离地面 m,则水流落地点B离墙的距离OB是( )
A.2 m B.3 m C.4 m D.5 m
4. 如图,抛物线型的拱门的地面宽度为20米,两侧离地面15米处各有一个观光窗,两窗的水平距离为10米,则拱门的最大高度为( )
A.10米 B.15米 C.20米 D.30米
5.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段AB上离中点M 5米的地方,桥的高度是( )
A.12米 B.13米 C.14米 D.15米
6.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是40 m;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0 m/s;④小球的高度h=30 m时,t=1.5 s.其中正确的是( )
A.①④ B.①② C.②③④ D.②③
7.如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-k)2+h.已知球与O点的水平距离为6 m时,达到最高2.6 m,球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m,则下列判断正确的是( )
A.球不会过球网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定球能否过球网
二、填空题
8.如图,高腾同学在校运会跳高比赛中采用背跃式,跳跃路线是一条抛物线,他跳跃的高度y(单位:m)与跳跃时间x(单位:s)之间具有函数关系y=-x2+x+,那么他能跳过的最大高度为 m.
9.如图是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状的,抛物线两端点与水面的距离都是1米,拱桥的跨度为10米,桥洞与水面的最大距离是5米,桥洞两侧壁上各有一盏距离水面4米的景观灯.两盏景观灯之间的水平距离为 米.
10.如图所示,从O点正上方2 m的点A处向右上方抛一个小球P,小球运动的路线呈抛物线形状,该抛物线为L,小球与O点的水平距离为
2 m时达到最大高度6 m,然后落在下方台阶上弹起,已知MN=4 m,FM=DE=BC=1.2 m,ON=CD=EF=1 m,若小球弹起后的运动路线是一条与L形状相同的抛物线,且落点Q与B,D在同一直线上,则小球弹起后的最大高度是 m.
三、解答题
11.如图,一名垒球运动员进行投球训练,站在点O处开始投球,球出手的高度是2米,球运动的轨迹是抛物线,当球达到最高点E时,水平距离EG=20米,与地面的高度EF=6米,掷出的球恰好落在训练墙AB上B点的位置,AB=3米.
(1)求抛物线的函数关系式;
(2)求点O到训练墙AB的距离(OA的长度).
12.有一个抛物线形的桥洞,桥洞离水面的最大高度为4 m,跨度为12 m.现将它放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式;
(2)一艘宽为4米,高出水面3米的货船能否从此桥洞通过
13.某篮球队员的一次投篮命中,篮球从出手到命中行进的轨迹可以近似看作抛物线的一部分,表示篮球距地面的高度y(单位:m)与行进的水平距离x(单位:m)之间关系的图象如图所示.已知篮球出手位置A与篮筐的水平距离为4.5 m,篮筐距地面的高度为3.05 m,当篮球行进的水平距离为3 m时,篮球距地面的高度达到最大,为3.3 m.
(1)图中点B表示篮筐,其坐标为 ,篮球行进的最高点C的坐标为 ;
(2)求篮球出手时距地面的高度.
答案全解全析
一、选择题
1.答案 B 设抛物线的表达式为y=ax2(a≠0),将B(45,-78)代入得-78=a×452,解得a=-,故此抛物线型钢拱的函数表达式为y=-x2.故选B.
2.答案 C 由题意得14=x2+5,解得x=±,∴A,C,
∴AC=-=9,故选C.
3.答案 B 如图,建立平面直角坐标系,则抛物线的顶点M的坐标为,A点坐标为(0,10).设抛物线的解析式为y=a(x-1)2+,将A(0,10)代入得10=a+,解得a=-.∴抛物线的解析式为y=-(x-1)2+.当y=0时,0=-(x-1)2+,解得x1=-1(舍去),x2=3.∴OB=3 m.故选B.
4.答案 C 如图所示,以线段CD所在直线为x轴,线段CD的垂直平分线为y轴建立平面直角坐标系,此时,抛物线与 x 轴的交点为 C(-10,0),D(10,0),设这条抛物线的解析式为 y=a(x-10)·(x+10),∵抛物线经过点 B(5,15),∴15=a(5-10)×(5+10),解得a=-,∴y=-(x-10)(x+10)=-x2+20,∴当x=0时,y取得最大值,此时y=20,即拱门的最大高度是20米.故选C.
5. 答案 D 如图,以M为坐标原点,AB所在直线为x轴,建立平面直角坐标系,∵桥的最大高度是16米,跨度是40米,∴C(0,16),A(-20,0),B(20,0),设抛物线解析式为y=ax2+16,将A(-20,0)代入得0=400a+16,解得a=-,∴抛物线解析式为y=-x2+16,当x=5时,y=-×52+16=-1+16=15,∴在线段AB上离中点M 5米的地方,桥的高度是15米.
6. 答案 D ①由图象知小球在空中达到的最大高度是40 m,经过的路程是40×2=80(m),故①错误;②小球抛出3秒后开始下降,速度越来越快,故②正确;③小球抛出3秒时达到最高点,速度为0 m/s,故③正确;④设函数解析式为h=a(t-3)2+40,把O(0,0)代入得0=a(0-3)2+40,解得a=-,∴函数解析式为h=-(t-3)2+40,把h=30代入解析式,得30=-(t-3)2+40,解得t=4.5或t=1.5,∴小球的高度h=30 m时,t=1.5 s或4.5 s,故④错误.故选D.
7. 答案 C ∵球与O点的水平距离为6 m时,达到最高2.6 m,
∴抛物线为y=a(x-6)2+2.6.
∵抛物线y=a(x-6)2+2.6过点(0,2),∴2=a(0-6)2+2.6,解得a=-,故y与x的关系式为y=-(x-6)2+2.6,当x=9时,y=-×(9-6)2+2.6=2.45>2.43,所以球能过球网;当y=0时,-(x-6)2+2.6=0,解得x1=6+2>18,x2=6-2(舍去),故会出界.
二、填空题
8.答案
解析 ∵y=-x2+x+=-(x-1)2+,∴他能跳过的最大高度为m.
9.答案 5
解析 建立平面直角坐标系如图所示,则抛物线的顶点坐标为(5,5),且经过点(0,1),设抛物线的解析式为y=a(x-5)2+5(a≠0),把点(0,1)代入得1=a(0-5)2+5,解得a=-,∴抛物线的解析式为y=-(x-5)2+5.令y=4,可解得x1=,x2=,∴两盏景观灯之间的水平距离是-=5米.
10.答案
解析 建立平面直角坐标系如图所示,
则A(0,2),B(4.6,2),C(3.4,2),D(3.4,3),抛物线L的顶点为(2,6).设抛物线L的解析式为y=a(x-2)2+6,
把点A(0,2)代入得,4a+6=2,解得a=-1.
∵抛物线L的对称轴为直线x=2,
∴点A关于该对称轴的对称点为(4,2),
∴小球落在BC上.设直线BD的解析式为y=kx+b,
∴解得
∴直线BD的解析式为y=-x+,令y=0,则x=7,
∴Q(7,0).
∵小球弹起后的运动路线是一条与L形状相同的抛物线,
∴设弹起后的抛物线的解析式为y=-x2+mx+n,
把(4,2),(7,0)代入得解得
∴弹起后的抛物线的解析式为y=-x2+x-=-+,
∴小球弹起后的最大高度为 m.
三、解答题
11.解析 (1)由题意得,E(20,6)和C(0,2),
设抛物线的函数关系式为y=a(x-20)2+6,
∴2=a(0-20)2+6,
解得a=-0.01,
∴抛物线的函数关系式为y=-0.01(x-20)2+6.
(2)当y=3时,3=-0.01(x-20)2+6,
解得x1=20+10,x2=20-10(舍去).
答:点O到训练墙AB的距离(OA的长度)为(20+10)米.
12.解析 (1)由图象可知抛物线的顶点坐标为(6,4),过点(12,0),
设抛物线的解析式为y=a(x-6)2+4,
则0=a(12-6)2+4,解得a=-,
即这条抛物线的解析式为y=-(x-6)2+4.
(2)当x=×(12-4)=4时,y=-×(4-6)2+4=>3,∴货船能通过此桥洞.
13.解析 (1)(4.5,3.05);(3,3.3).
(2)设抛物线的解析式为y=a(x-3)2+3.3,
把B(4.5,3.05)代入得,3.05=a(4.5-3)2+3.3,
解得a=-,
∴抛物线的解析式为y=-(x-3)2+3.3,
当x=0时,y=2.3.
答:篮球出手时距地面的高度为2.3米.
班级 姓名
第二十二章 二次函数
22.3 实际问题与二次函数
第3课时 实物抛物线问题
一、选择题
1. 北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线型钢拱的函数表达式为( )
A.y=x2 B.y=-x2 C.y=x2 D.y=-x2
2. 如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线y=x2+5的一部分,则杯口的口径AC=( )
A.7 B.8 C.9 D.10
3. 如图,从某建筑物10 m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1 m,离地面 m,则水流落地点B离墙的距离OB是( )
A.2 m B.3 m C.4 m D.5 m
4. 如图,抛物线型的拱门的地面宽度为20米,两侧离地面15米处各有一个观光窗,两窗的水平距离为10米,则拱门的最大高度为( )
A.10米 B.15米 C.20米 D.30米
5.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段AB上离中点M 5米的地方,桥的高度是( )
A.12米 B.13米 C.14米 D.15米
6.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是40 m;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0 m/s;④小球的高度h=30 m时,t=1.5 s.其中正确的是( )
A.①④ B.①② C.②③④ D.②③
7.如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-k)2+h.已知球与O点的水平距离为6 m时,达到最高2.6 m,球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m,则下列判断正确的是( )
A.球不会过球网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定球能否过球网
二、填空题
8.如图,高腾同学在校运会跳高比赛中采用背跃式,跳跃路线是一条抛物线,他跳跃的高度y(单位:m)与跳跃时间x(单位:s)之间具有函数关系y=-x2+x+,那么他能跳过的最大高度为 m.
9.如图是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状的,抛物线两端点与水面的距离都是1米,拱桥的跨度为10米,桥洞与水面的最大距离是5米,桥洞两侧壁上各有一盏距离水面4米的景观灯.两盏景观灯之间的水平距离为 米.
10.如图所示,从O点正上方2 m的点A处向右上方抛一个小球P,小球运动的路线呈抛物线形状,该抛物线为L,小球与O点的水平距离为
2 m时达到最大高度6 m,然后落在下方台阶上弹起,已知MN=4 m,FM=DE=BC=1.2 m,ON=CD=EF=1 m,若小球弹起后的运动路线是一条与L形状相同的抛物线,且落点Q与B,D在同一直线上,则小球弹起后的最大高度是 m.
三、解答题
11.如图,一名垒球运动员进行投球训练,站在点O处开始投球,球出手的高度是2米,球运动的轨迹是抛物线,当球达到最高点E时,水平距离EG=20米,与地面的高度EF=6米,掷出的球恰好落在训练墙AB上B点的位置,AB=3米.
(1)求抛物线的函数关系式;
(2)求点O到训练墙AB的距离(OA的长度).
12.有一个抛物线形的桥洞,桥洞离水面的最大高度为4 m,跨度为12 m.现将它放在如图所示的直角坐标系中.
(1)求这条抛物线的解析式;
(2)一艘宽为4米,高出水面3米的货船能否从此桥洞通过
13.某篮球队员的一次投篮命中,篮球从出手到命中行进的轨迹可以近似看作抛物线的一部分,表示篮球距地面的高度y(单位:m)与行进的水平距离x(单位:m)之间关系的图象如图所示.已知篮球出手位置A与篮筐的水平距离为4.5 m,篮筐距地面的高度为3.05 m,当篮球行进的水平距离为3 m时,篮球距地面的高度达到最大,为3.3 m.
(1)图中点B表示篮筐,其坐标为 ,篮球行进的最高点C的坐标为 ;
(2)求篮球出手时距地面的高度.
答案全解全析
一、选择题
1.答案 B 设抛物线的表达式为y=ax2(a≠0),将B(45,-78)代入得-78=a×452,解得a=-,故此抛物线型钢拱的函数表达式为y=-x2.故选B.
2.答案 C 由题意得14=x2+5,解得x=±,∴A,C,
∴AC=-=9,故选C.
3.答案 B 如图,建立平面直角坐标系,则抛物线的顶点M的坐标为,A点坐标为(0,10).设抛物线的解析式为y=a(x-1)2+,将A(0,10)代入得10=a+,解得a=-.∴抛物线的解析式为y=-(x-1)2+.当y=0时,0=-(x-1)2+,解得x1=-1(舍去),x2=3.∴OB=3 m.故选B.
4.答案 C 如图所示,以线段CD所在直线为x轴,线段CD的垂直平分线为y轴建立平面直角坐标系,此时,抛物线与 x 轴的交点为 C(-10,0),D(10,0),设这条抛物线的解析式为 y=a(x-10)·(x+10),∵抛物线经过点 B(5,15),∴15=a(5-10)×(5+10),解得a=-,∴y=-(x-10)(x+10)=-x2+20,∴当x=0时,y取得最大值,此时y=20,即拱门的最大高度是20米.故选C.
5. 答案 D 如图,以M为坐标原点,AB所在直线为x轴,建立平面直角坐标系,∵桥的最大高度是16米,跨度是40米,∴C(0,16),A(-20,0),B(20,0),设抛物线解析式为y=ax2+16,将A(-20,0)代入得0=400a+16,解得a=-,∴抛物线解析式为y=-x2+16,当x=5时,y=-×52+16=-1+16=15,∴在线段AB上离中点M 5米的地方,桥的高度是15米.
6. 答案 D ①由图象知小球在空中达到的最大高度是40 m,经过的路程是40×2=80(m),故①错误;②小球抛出3秒后开始下降,速度越来越快,故②正确;③小球抛出3秒时达到最高点,速度为0 m/s,故③正确;④设函数解析式为h=a(t-3)2+40,把O(0,0)代入得0=a(0-3)2+40,解得a=-,∴函数解析式为h=-(t-3)2+40,把h=30代入解析式,得30=-(t-3)2+40,解得t=4.5或t=1.5,∴小球的高度h=30 m时,t=1.5 s或4.5 s,故④错误.故选D.
7. 答案 C ∵球与O点的水平距离为6 m时,达到最高2.6 m,
∴抛物线为y=a(x-6)2+2.6.
∵抛物线y=a(x-6)2+2.6过点(0,2),∴2=a(0-6)2+2.6,解得a=-,故y与x的关系式为y=-(x-6)2+2.6,当x=9时,y=-×(9-6)2+2.6=2.45>2.43,所以球能过球网;当y=0时,-(x-6)2+2.6=0,解得x1=6+2>18,x2=6-2(舍去),故会出界.
二、填空题
8.答案
解析 ∵y=-x2+x+=-(x-1)2+,∴他能跳过的最大高度为m.
9.答案 5
解析 建立平面直角坐标系如图所示,则抛物线的顶点坐标为(5,5),且经过点(0,1),设抛物线的解析式为y=a(x-5)2+5(a≠0),把点(0,1)代入得1=a(0-5)2+5,解得a=-,∴抛物线的解析式为y=-(x-5)2+5.令y=4,可解得x1=,x2=,∴两盏景观灯之间的水平距离是-=5米.
10.答案
解析 建立平面直角坐标系如图所示,
则A(0,2),B(4.6,2),C(3.4,2),D(3.4,3),抛物线L的顶点为(2,6).设抛物线L的解析式为y=a(x-2)2+6,
把点A(0,2)代入得,4a+6=2,解得a=-1.
∵抛物线L的对称轴为直线x=2,
∴点A关于该对称轴的对称点为(4,2),
∴小球落在BC上.设直线BD的解析式为y=kx+b,
∴解得
∴直线BD的解析式为y=-x+,令y=0,则x=7,
∴Q(7,0).
∵小球弹起后的运动路线是一条与L形状相同的抛物线,
∴设弹起后的抛物线的解析式为y=-x2+mx+n,
把(4,2),(7,0)代入得解得
∴弹起后的抛物线的解析式为y=-x2+x-=-+,
∴小球弹起后的最大高度为 m.
三、解答题
11.解析 (1)由题意得,E(20,6)和C(0,2),
设抛物线的函数关系式为y=a(x-20)2+6,
∴2=a(0-20)2+6,
解得a=-0.01,
∴抛物线的函数关系式为y=-0.01(x-20)2+6.
(2)当y=3时,3=-0.01(x-20)2+6,
解得x1=20+10,x2=20-10(舍去).
答:点O到训练墙AB的距离(OA的长度)为(20+10)米.
12.解析 (1)由图象可知抛物线的顶点坐标为(6,4),过点(12,0),
设抛物线的解析式为y=a(x-6)2+4,
则0=a(12-6)2+4,解得a=-,
即这条抛物线的解析式为y=-(x-6)2+4.
(2)当x=×(12-4)=4时,y=-×(4-6)2+4=>3,∴货船能通过此桥洞.
13.解析 (1)(4.5,3.05);(3,3.3).
(2)设抛物线的解析式为y=a(x-3)2+3.3,
把B(4.5,3.05)代入得,3.05=a(4.5-3)2+3.3,
解得a=-,
∴抛物线的解析式为y=-(x-3)2+3.3,
当x=0时,y=2.3.
答:篮球出手时距地面的高度为2.3米.
同课章节目录
