2022-2023学年人教版数学九年级上册 22.3.1 图形面积问题 章节培优训练试卷 (含解析)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册 22.3.1 图形面积问题 章节培优训练试卷 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 08:32:12 | ||
图片预览



文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十二章 二次函数
22.3 实际问题与二次函数
第1课时 图形面积问题
一、选择题
1. 用长为4米的绳子围成一个矩形,它的一边长为x米,设它的面积为S平方米,则S与x的函数关系为( )
A.正比例函数关系
B.一次函数关系
C.二次函数关系
D.以上都不是
2. 如图,将一根长2 m的铁丝首尾相接围成矩形,则围成的矩形的面积最大是( )
A. m2 B. m2
C. m2 D.1 m2
3. 如图,有一个矩形苗圃,其中一边靠墙,另外三边用长为20 m的篱笆围成.已知墙长为15 m,若平行于墙的一边长不小于8 m,则这个苗圃面积的最大值和最小值分别为( )
A.48 m2,37.5 m2
B.50 m2,32 m2
C.50 m2,37.5 m2
D.48 m2,32 m2
4. 为了节省材料,某工厂利用岸堤MN(岸堤足够长)为一边,用总长为80米的材料围成一个由三块面积相等的小长方形组成的长方形区域(图中长方形ABCD),若BC=(x+20)米,则下列4个结论:①AB=(10-1.5x)米;②BC=2CF;③AE=2BE;④长方形ABCD的最大面积为300平方米.其中正确结论的序号是( )
A.①② B.①③
C.②③ D.③④
5.如图,将一根长2 m的铁丝首尾相接围成矩形,则围成的矩形的面积的最大值是( )
A. m2 B. m2 C. m2 D.1 m2
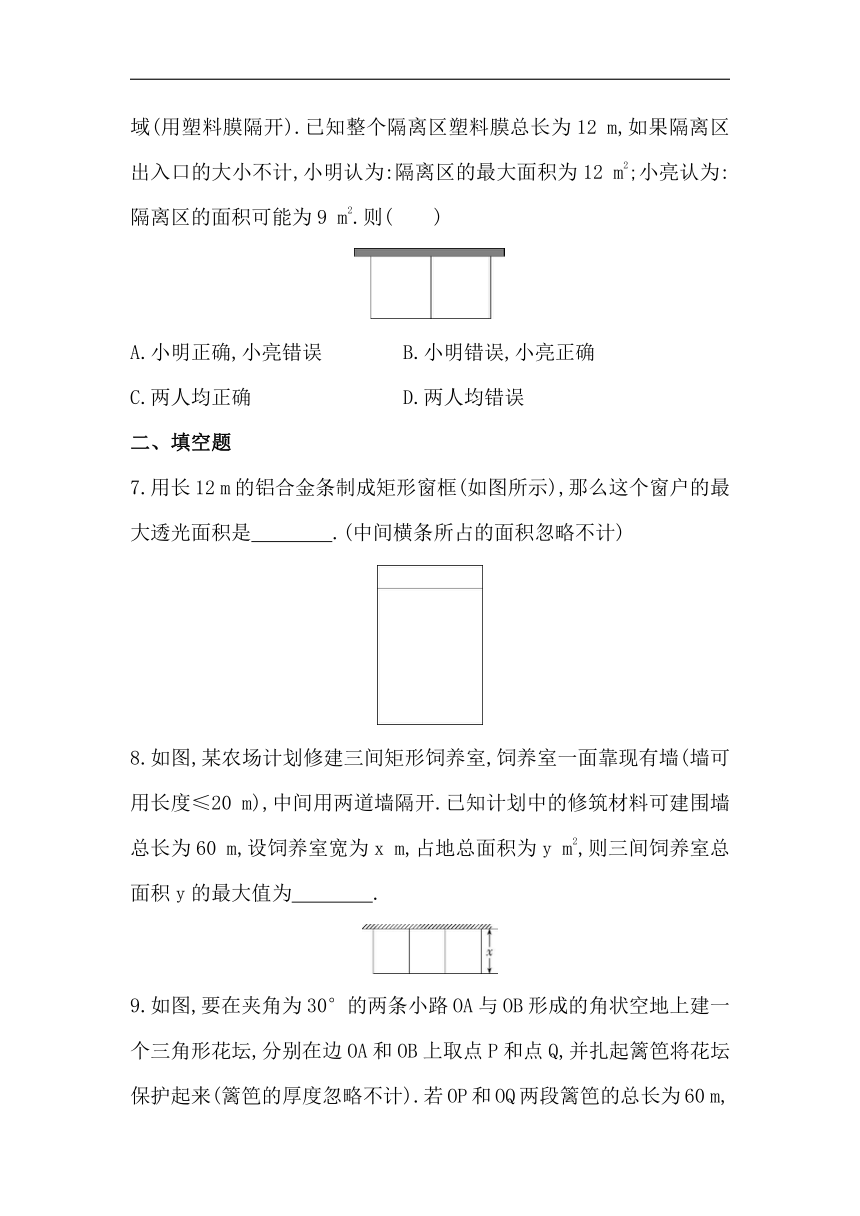
6.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个矩形临时隔离区,隔离区一面靠长为5 m的墙,隔离区被分成两个矩形区域(用塑料膜隔开).已知整个隔离区塑料膜总长为12 m,如果隔离区出入口的大小不计,小明认为:隔离区的最大面积为12 m2;小亮认为:隔离区的面积可能为9 m2.则( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
二、填空题
7.用长12 m的铝合金条制成矩形窗框(如图所示),那么这个窗户的最大透光面积是 .(中间横条所占的面积忽略不计)
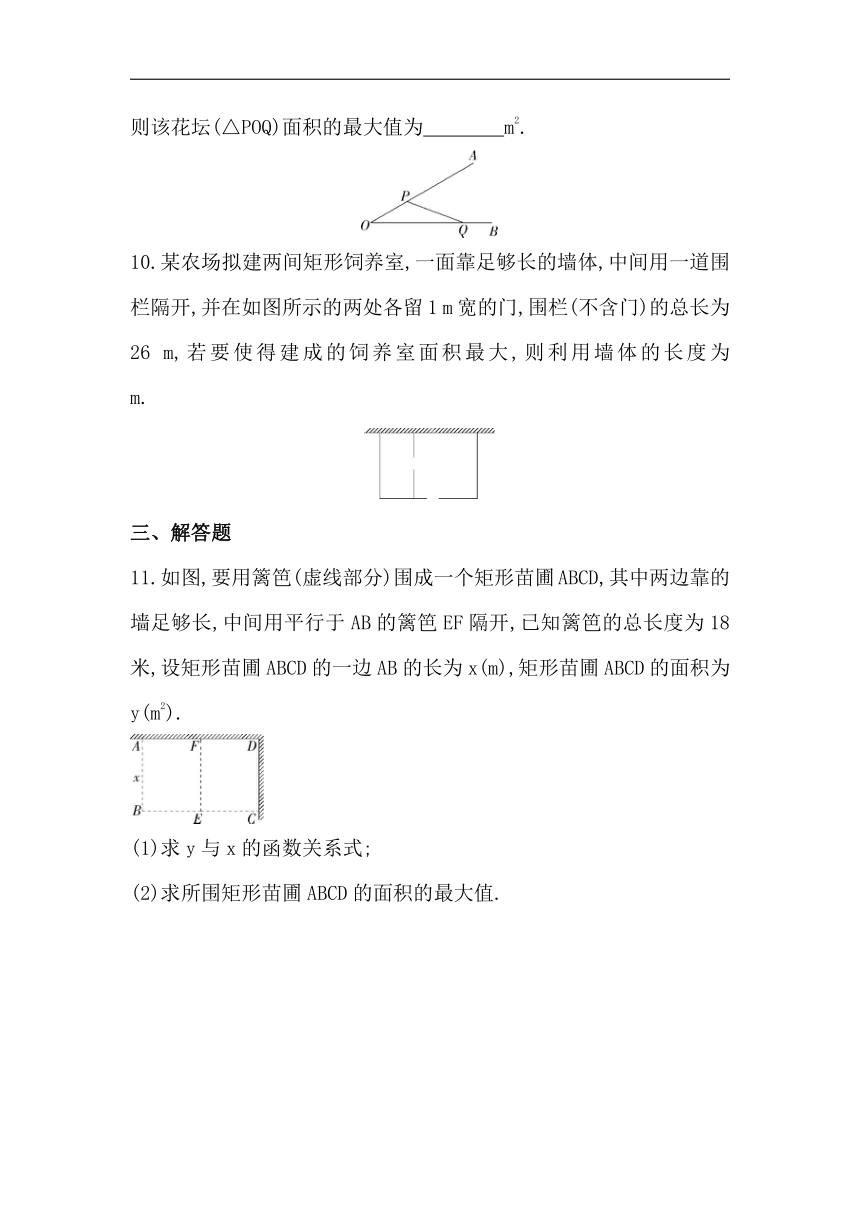
8.如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙(墙可用长度≤20 m),中间用两道墙隔开.已知计划中的修筑材料可建围墙总长为60 m,设饲养室宽为x m,占地总面积为y m2,则三间饲养室总面积y的最大值为 .
9.如图,要在夹角为30°的两条小路OA与OB形成的角状空地上建一个三角形花坛,分别在边OA和OB上取点P和点Q,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若OP和OQ两段篱笆的总长为60 m,则该花坛(△POQ)面积的最大值为 m2.
10.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1 m宽的门,围栏(不含门)的总长为26 m,若要使得建成的饲养室面积最大,则利用墙体的长度为 m.
三、解答题
11.如图,要用篱笆(虚线部分)围成一个矩形苗圃ABCD,其中两边靠的墙足够长,中间用平行于AB的篱笆EF隔开,已知篱笆的总长度为18米,设矩形苗圃ABCD的一边AB的长为x(m),矩形苗圃ABCD的面积为y(m2).
(1)求y与x的函数关系式;
(2)求所围矩形苗圃ABCD的面积的最大值.
12.某社区决定把一块长为50 m、宽为30 m的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于14 m,不大于26 m,设绿化区较长边的长为x m,活动区的面积为y m2.
(1)求y与x的函数表达式并求出自变量x的取值范围;
(2)求活动区的最大面积.
答案全解全析
一、选择题
1.答案 C ∵矩形的周长为4米,一边长为x米,
∴其邻边长为(2-x)米,∴S=x(2-x)=-x2+2x,∴S与x的函数关系为二次函数关系.故选C.
2.答案 A 设矩形的一边长为x m,则其邻边长为(1-x)m,设矩形的面积为S m2,则S=x(1-x)=-x2+x=-+,∵03.答案 C 设平行于墙的一边长为x m,苗圃面积为S m2,则S=x×(20-x)=
-(x2-20x)=-(x-10)2+50(8≤x≤15),易知当x=10时,S有最大值,
S最大=50.∵15-10>10-8,∴当x=15时,S有最小值,
S最小=15××(20-15)=37.5,
∴这个苗圃面积的最大值和最小值分别为50 m2,37.5 m2.故选C.
答案 D ∵三块小长方形的面积相等,∴EG=GF,设EG=FG=a,AE=HG=DF=b,则EF=BC=2a,故BE=FC=b,无法得出BC=2CF,故②错误;可得AE=2BE,故③正确;可得b+b+b+b+b=80-2(x+20),解得b=10-x,则AB==米,故①错误;设长方形ABCD的面积为S平方米,则S=(20+x)=-x2+300,
∵-x2≤0,∴当x=0,即BC=20米时,S取得最大值,为300,故④正确.故选D.
5. 答案 A 设矩形的一边长为x m,则其邻边长为(1-x)m.设矩形的面积为S m2,则S=x(1-x)=-x2+x=-+(06. 答案 B 设平行于墙的塑料膜的长度为x m,隔离区的面积为S m2,由题意得S=×x=
-x2+4x(04×5=-+20=.∵<12,∴小明错误.令S=9,得9=-x2+4x,解得x1=9(舍),x2=3,∴x=3时,S=9.∴隔离区的面积可能为9 m2,即小亮正确.
二、填空题
7.答案 6 m2
解析 设窗户的高度为x m,窗户的透光面积为S m2,则宽为m,由矩形面积公式得S=·x=-x2+4x=-(x-3)2+6,∵x>0,>0,∴08.答案 200
解析 若饲养室宽为x m,则长为(60-4x)m,
∴y=x(60-4x)=-4x2+60x=-4(x-7.5)2+225,
∵0<60-4x≤20,∴10≤x<15.∵-4<0,∴当x>7.5时,y随x的增大而减小,∴当x=10时,y有最大值,最大值为-4×102+60×10=200.
9. 答案 225
解析 如图,作PC⊥OB于点C,设OP长为x m,△POQ的面积为S m2.则OQ长为(60-x)m,∵∠POQ=30°,∴PC=OP=x(m),∴S=×x·(60-x)=-(x-30)2+225(010. 答案 14
解析 所有围栏的长加上两个门的宽为26+2=28(m),设平行于墙的围栏的长与一个门的宽的和为x m,则垂直于墙的围栏长为(28-x)m,设建成的饲养室的面积为S m2,则S=x(28-x)=-(x2-28x)=-(x-14)2+,∴当x=14时,建成的饲养室面积最大,则利用墙体的长度为14 m.
三、解答题
11.解析 (1)若AB=x m,则有BC=(18-2x)m,
根据题意得y=x(18-2x)=-2x2+18x,
∴y与x的函数关系式为y=-2x2+18x.
(2)∵0<18-2x,x>0,∴0∵y=-2x2+18x=-2+中,-2<0,∴y有最大值,
当x=时,y取得最大值,为.
答:所围矩形苗圃ABCD的面积的最大值为 m2.
12.解析 (1)根据题意,绿化区的宽为[30-(50-2x)]÷2=(x-10)m,
∴y=50×30-4x(x-10)=-4x2+40x+1 500,
∵四个出口宽度相同,其宽度不小于14 m,不大于26 m,
即14≤50-2x≤26,
∴12≤x≤18,
∴y与x的函数表达式为y=-4x2+40x+1 500(12≤x≤18).
(2)y=-4x2+40x+1 500=-4(x-5)2+1 600,
∵-4<0,∴抛物线的开口向下,
当x≥5时,y随x的增大而减小,
∵12≤x≤18,
∴当x=12时,y有最大值,最大值为1 404.
答:活动区的最大面积为1 404 m2.
班级 姓名
第二十二章 二次函数
22.3 实际问题与二次函数
第1课时 图形面积问题
一、选择题
1. 用长为4米的绳子围成一个矩形,它的一边长为x米,设它的面积为S平方米,则S与x的函数关系为( )
A.正比例函数关系
B.一次函数关系
C.二次函数关系
D.以上都不是
2. 如图,将一根长2 m的铁丝首尾相接围成矩形,则围成的矩形的面积最大是( )
A. m2 B. m2
C. m2 D.1 m2
3. 如图,有一个矩形苗圃,其中一边靠墙,另外三边用长为20 m的篱笆围成.已知墙长为15 m,若平行于墙的一边长不小于8 m,则这个苗圃面积的最大值和最小值分别为( )
A.48 m2,37.5 m2
B.50 m2,32 m2
C.50 m2,37.5 m2
D.48 m2,32 m2
4. 为了节省材料,某工厂利用岸堤MN(岸堤足够长)为一边,用总长为80米的材料围成一个由三块面积相等的小长方形组成的长方形区域(图中长方形ABCD),若BC=(x+20)米,则下列4个结论:①AB=(10-1.5x)米;②BC=2CF;③AE=2BE;④长方形ABCD的最大面积为300平方米.其中正确结论的序号是( )
A.①② B.①③
C.②③ D.③④
5.如图,将一根长2 m的铁丝首尾相接围成矩形,则围成的矩形的面积的最大值是( )
A. m2 B. m2 C. m2 D.1 m2
6.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个矩形临时隔离区,隔离区一面靠长为5 m的墙,隔离区被分成两个矩形区域(用塑料膜隔开).已知整个隔离区塑料膜总长为12 m,如果隔离区出入口的大小不计,小明认为:隔离区的最大面积为12 m2;小亮认为:隔离区的面积可能为9 m2.则( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
二、填空题
7.用长12 m的铝合金条制成矩形窗框(如图所示),那么这个窗户的最大透光面积是 .(中间横条所占的面积忽略不计)
8.如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙(墙可用长度≤20 m),中间用两道墙隔开.已知计划中的修筑材料可建围墙总长为60 m,设饲养室宽为x m,占地总面积为y m2,则三间饲养室总面积y的最大值为 .
9.如图,要在夹角为30°的两条小路OA与OB形成的角状空地上建一个三角形花坛,分别在边OA和OB上取点P和点Q,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若OP和OQ两段篱笆的总长为60 m,则该花坛(△POQ)面积的最大值为 m2.
10.某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的两处各留1 m宽的门,围栏(不含门)的总长为26 m,若要使得建成的饲养室面积最大,则利用墙体的长度为 m.
三、解答题
11.如图,要用篱笆(虚线部分)围成一个矩形苗圃ABCD,其中两边靠的墙足够长,中间用平行于AB的篱笆EF隔开,已知篱笆的总长度为18米,设矩形苗圃ABCD的一边AB的长为x(m),矩形苗圃ABCD的面积为y(m2).
(1)求y与x的函数关系式;
(2)求所围矩形苗圃ABCD的面积的最大值.
12.某社区决定把一块长为50 m、宽为30 m的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于14 m,不大于26 m,设绿化区较长边的长为x m,活动区的面积为y m2.
(1)求y与x的函数表达式并求出自变量x的取值范围;
(2)求活动区的最大面积.
答案全解全析
一、选择题
1.答案 C ∵矩形的周长为4米,一边长为x米,
∴其邻边长为(2-x)米,∴S=x(2-x)=-x2+2x,∴S与x的函数关系为二次函数关系.故选C.
2.答案 A 设矩形的一边长为x m,则其邻边长为(1-x)m,设矩形的面积为S m2,则S=x(1-x)=-x2+x=-+,∵0
-(x2-20x)=-(x-10)2+50(8≤x≤15),易知当x=10时,S有最大值,
S最大=50.∵15-10>10-8,∴当x=15时,S有最小值,
S最小=15××(20-15)=37.5,
∴这个苗圃面积的最大值和最小值分别为50 m2,37.5 m2.故选C.
答案 D ∵三块小长方形的面积相等,∴EG=GF,设EG=FG=a,AE=HG=DF=b,则EF=BC=2a,故BE=FC=b,无法得出BC=2CF,故②错误;可得AE=2BE,故③正确;可得b+b+b+b+b=80-2(x+20),解得b=10-x,则AB==米,故①错误;设长方形ABCD的面积为S平方米,则S=(20+x)=-x2+300,
∵-x2≤0,∴当x=0,即BC=20米时,S取得最大值,为300,故④正确.故选D.
5. 答案 A 设矩形的一边长为x m,则其邻边长为(1-x)m.设矩形的面积为S m2,则S=x(1-x)=-x2+x=-+(0
-x2+4x(0
二、填空题
7.答案 6 m2
解析 设窗户的高度为x m,窗户的透光面积为S m2,则宽为m,由矩形面积公式得S=·x=-x2+4x=-(x-3)2+6,∵x>0,>0,∴0
解析 若饲养室宽为x m,则长为(60-4x)m,
∴y=x(60-4x)=-4x2+60x=-4(x-7.5)2+225,
∵0<60-4x≤20,∴10≤x<15.∵-4<0,∴当x>7.5时,y随x的增大而减小,∴当x=10时,y有最大值,最大值为-4×102+60×10=200.
9. 答案 225
解析 如图,作PC⊥OB于点C,设OP长为x m,△POQ的面积为S m2.则OQ长为(60-x)m,∵∠POQ=30°,∴PC=OP=x(m),∴S=×x·(60-x)=-(x-30)2+225(0
解析 所有围栏的长加上两个门的宽为26+2=28(m),设平行于墙的围栏的长与一个门的宽的和为x m,则垂直于墙的围栏长为(28-x)m,设建成的饲养室的面积为S m2,则S=x(28-x)=-(x2-28x)=-(x-14)2+,∴当x=14时,建成的饲养室面积最大,则利用墙体的长度为14 m.
三、解答题
11.解析 (1)若AB=x m,则有BC=(18-2x)m,
根据题意得y=x(18-2x)=-2x2+18x,
∴y与x的函数关系式为y=-2x2+18x.
(2)∵0<18-2x,x>0,∴0
当x=时,y取得最大值,为.
答:所围矩形苗圃ABCD的面积的最大值为 m2.
12.解析 (1)根据题意,绿化区的宽为[30-(50-2x)]÷2=(x-10)m,
∴y=50×30-4x(x-10)=-4x2+40x+1 500,
∵四个出口宽度相同,其宽度不小于14 m,不大于26 m,
即14≤50-2x≤26,
∴12≤x≤18,
∴y与x的函数表达式为y=-4x2+40x+1 500(12≤x≤18).
(2)y=-4x2+40x+1 500=-4(x-5)2+1 600,
∵-4<0,∴抛物线的开口向下,
当x≥5时,y随x的增大而减小,
∵12≤x≤18,
∴当x=12时,y有最大值,最大值为1 404.
答:活动区的最大面积为1 404 m2.
同课章节目录
