2022-2023学年 人教版九年级数学上册 23.2.1 中心对称 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年 人教版九年级数学上册 23.2.1 中心对称 章节培优训练试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 415.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 08:41:58 | ||
图片预览



文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十三章 旋转
23.2 中心对称
23.2.1 中心对称
一、选择题
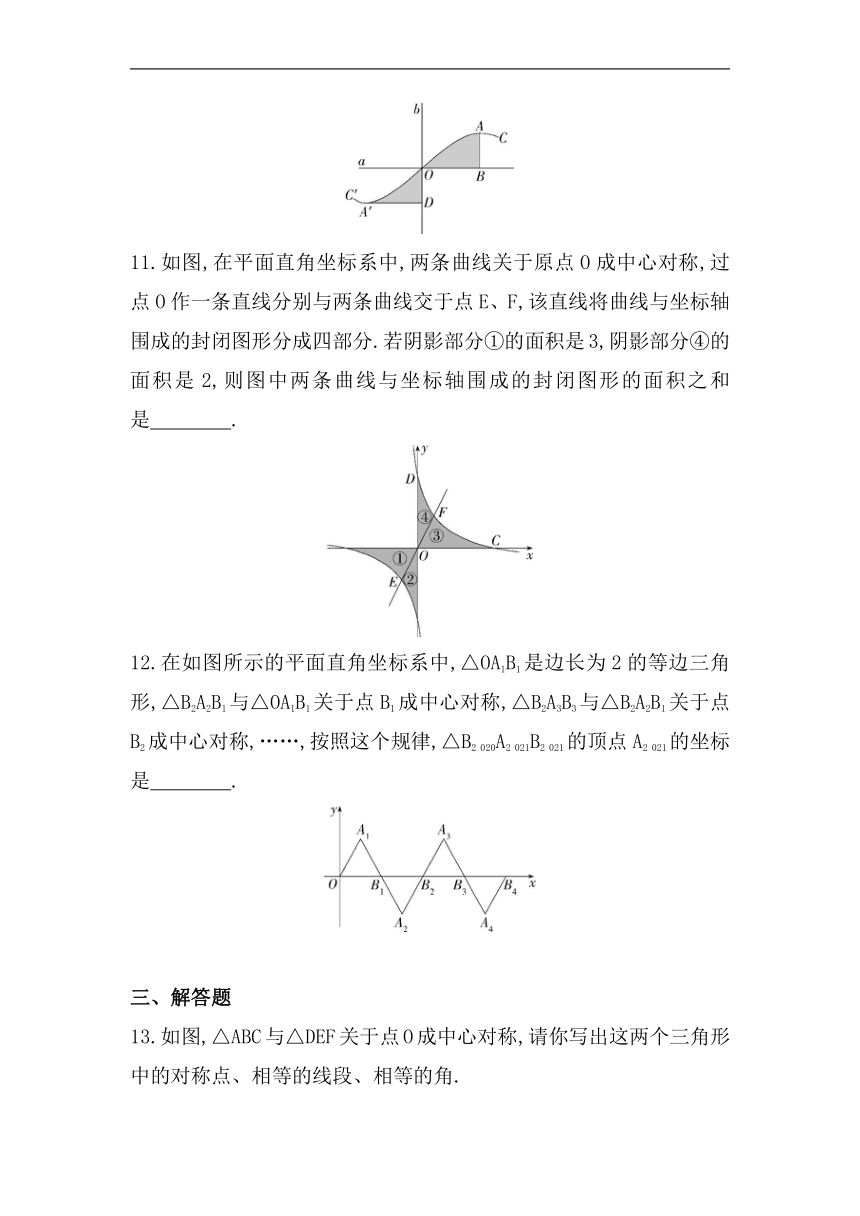
1. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2. 在平面直角坐标系xOy中,△ABC与△A'B'C'关于原点O成中心对称的是( )
A B
C D
3.如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是( )
A.AD∥EF,AB∥GF B.BO=GO
C.CD=HE,BC=GH D.DO=HO
4. 如图所示,已知△ABC与△CDA关于点O成中心对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1 B.2 C.3 D.4
5.如图,△ABC与△A'B'C'关于点O成中心对称,下列结论中不成立的是( )
A.OC=OC'
B.∠ABC=∠A'C'B'
C.点B的对称点是点B'
D.BC∥B'C'
二、填空题
6.如图,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是 ,点A的对称点是 ,点E的对称点是 .BD∥ 且BD= .连接A,F的线段经过 ,△ABD≌ .
7.如图,△AOB与△COD关于公共顶点O成中心对称,连接AD、BC,添加一个条件 ,使四边形ABCD为菱形.
8.如图,已知 AB=3,AC=1,∠D=90°,△DEC 与△ABC关于点C成中心对称,点F是DE的中点,连接CF,AE,则CF的长是 .
9.如图,矩形ABCD和矩形A'B'C'D关于点D成中心对称,已知AB=3,BC=4,则阴影部分的周长和是 .
10.如图,直线a、b垂直相交于点O,曲线OAC与曲线OA'C'关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D,若OB=5,OD=3,则阴影部分的面积为 .
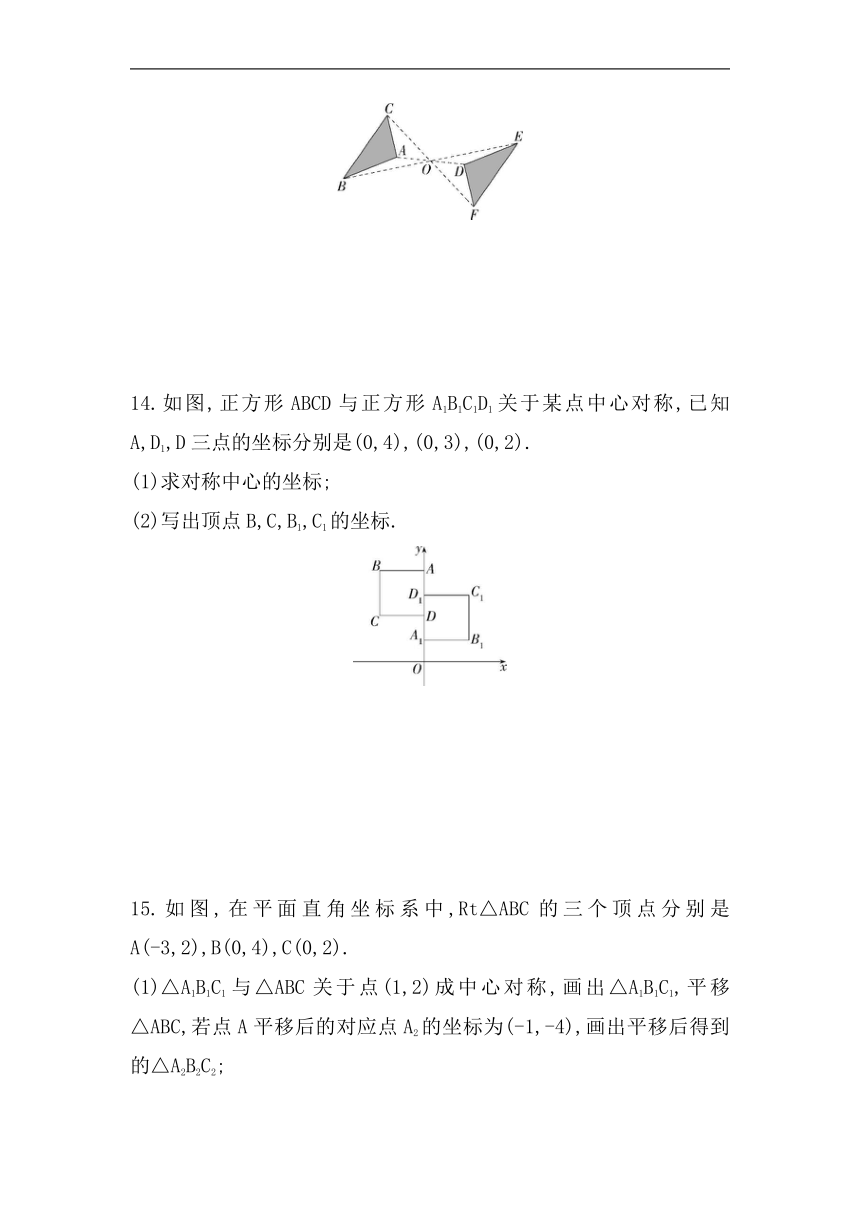
11.如图,在平面直角坐标系中,两条曲线关于原点O成中心对称,过点O作一条直线分别与两条曲线交于点E、F,该直线将曲线与坐标轴围成的封闭图形分成四部分.若阴影部分①的面积是3,阴影部分④的面积是2,则图中两条曲线与坐标轴围成的封闭图形的面积之和是 .
12.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,△B2A2B1与△OA1B1关于点B1成中心对称,△B2A3B3与△B2A2B1关于点B2成中心对称,……,按照这个规律,△B2 020A2 021B2 021的顶点A2 021的坐标是 .
三、解答题
13.如图,△ABC与△DEF关于点O成中心对称,请你写出这两个三角形中的对称点、相等的线段、相等的角.
14.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
15.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)△A1B1C1与△ABC关于点(1,2)成中心对称,画出△A1B1C1,平移△ABC,若点A平移后的对应点A2的坐标为(-1,-4),画出平移后得到的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
答案全解全析
一、选择题
1.答案 C 根据中心对称的概念,知(2)(3)(4)都成中心对称.故选C.
2.答案 D 选项A,△ABC与△A'B'C'关于y轴对称,故选项A不符合题意;选项B,△ABC与△A'B'C'关于x轴对称,故选项B不符合题意;选项C,△ABC与△A'B'C'关于点成中心对称,故选项C不符合题意;选项D,△ABC与△A'B'C'关于原点成中心对称,故选项D符合题意.故选D.
3.答案 D 选项A中,∵AD与EF关于点O成中心对称,∴AD∥EF,同理可得AB∥GF,所以说法正确;选项B中,∵B与G关于点O成中心对称,∴BO=GO,所以说法正确;选项C中,∵CD与HE关于点O成中心对称,∴CD=HE,同理可得BC=GH,所以说法正确;选项D中,根据题中条件无法证明DO=HO,故说法错误.故选D.
4.答案 D △ABC与△CDA关于点O成中心对称,则AB=CD,AD=BC,所以四边形ABCD是平行四边形,可知:①点E和点F,点B和点D是对称点,正确;②直线BD必经过点O,正确;③四边形DEOC与四边形BFOA的面积必相等,正确;④△AOE与△COF成中心对称,正确,故正确的个数为4.故选D.
5. 答案 B ∵△ABC与△A'B'C'关于点O成中心对称,
∴OC=OC',BC∥B'C',点B的对称点是点B',故A,C,D正确.故选B.
二、填空题
6.答案 点C;点F;点D;EG;EG;点C;△FGE
解析 四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是点C,点A的对称点是点F,点E的对称点是点D.BD∥EG且BD=EG.连接A,F的线段经过点C,△ABD≌△FGE.
7.答案 ∠AOB=90°(答案不唯一)
解析 ∵△AOB与△COD关于公共顶点O成中心对称,∴点A、O、C在一条直线上,点B、O、D在一条直线上,且AO=OC,BO=DO,∴四边形ABCD是平行四边形.当∠AOB=90°时,平行四边形ABCD是菱形,答案不唯一.
8.答案
解析 ∵△DEC 与△ABC关于点C成中心对称,∴DC=AC=1,DE=AB=3,∴在Rt△EDA中,AE==.∵点F是DE的中点,AC=DC,∴CF是△ADE的中位线,∴CF=AE=.
9.答案 48
解析 ∵四边形ABCD是矩形,∴∠B=90°.
∵AB=3,BC=4,∴AC===5,∴△ABC的周长=3+4+5=12.
∵矩形ABCD和矩形A'B'C'D关于点D成中心对称,∴阴影部分的四个直角三角形全等,∴阴影部分的周长和=4×12=48.
10. 答案 15
解析 如图,作AE⊥b于点E,由题可知,四边形ABOE为矩形,图形①与图形②的面积相等,AB=OD=3,∴阴影部分的面积=矩形ABOE的面积=3×5=15.
11. 答案 10
解析 两条曲线关于点O成中心对称,则阴影部分①和③关于点O成中心对称,阴影部分②和④关于点O成中心对称,∴封闭图形的面积之和是(2+3)×2=10.
12. 答案 (4 041,)
解析 ∵△OA1B1是边长为2的等边三角形,∴A1的坐标为(1,),B1的坐标为(2,0).∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∴点A2的坐标是(3,-).同理可得,点A3的坐标是(5,),点A4的坐标是
(7,-),……,∵1=2×1-1,3=2×2-1,5=2×3-1,7=2×4-1,……,∴点An的横坐标是2n-1,又∵当n为奇数时,点An的纵坐标是,当n为偶数时,点An的纵坐标是
-,∴△B2 020A2 021B2 021的顶点A2 021的横坐标是2×2 021-1=4 041,纵坐标是.
三、解答题
13.解析 对称点:A和D,B和E,C和F;
相等的线段:AC=DF,AB=DE,BC=EF;
相等的角:∠CAB=∠FDE,∠ABC=∠DEF,∠BCA=∠EFD.
14.解析 (1)根据中心对称的性质,可得对称中心是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是4-2=2,
∴B,C的坐标分别是(-2,4),(-2,2).
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3).
综上可得,顶点B,C,B1,C1的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
15.解析 (1)△A1B1C1如图所示,△A2B2C2如图所示.
(2)旋转中心的坐标为(2,-1).
班级 姓名
第二十三章 旋转
23.2 中心对称
23.2.1 中心对称
一、选择题
1. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2. 在平面直角坐标系xOy中,△ABC与△A'B'C'关于原点O成中心对称的是( )
A B
C D
3.如图,四边形ABCD与四边形FGHE关于点O成中心对称,下列说法中错误的是( )
A.AD∥EF,AB∥GF B.BO=GO
C.CD=HE,BC=GH D.DO=HO
4. 如图所示,已知△ABC与△CDA关于点O成中心对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1 B.2 C.3 D.4
5.如图,△ABC与△A'B'C'关于点O成中心对称,下列结论中不成立的是( )
A.OC=OC'
B.∠ABC=∠A'C'B'
C.点B的对称点是点B'
D.BC∥B'C'
二、填空题
6.如图,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是 ,点A的对称点是 ,点E的对称点是 .BD∥ 且BD= .连接A,F的线段经过 ,△ABD≌ .
7.如图,△AOB与△COD关于公共顶点O成中心对称,连接AD、BC,添加一个条件 ,使四边形ABCD为菱形.
8.如图,已知 AB=3,AC=1,∠D=90°,△DEC 与△ABC关于点C成中心对称,点F是DE的中点,连接CF,AE,则CF的长是 .
9.如图,矩形ABCD和矩形A'B'C'D关于点D成中心对称,已知AB=3,BC=4,则阴影部分的周长和是 .
10.如图,直线a、b垂直相交于点O,曲线OAC与曲线OA'C'关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D,若OB=5,OD=3,则阴影部分的面积为 .
11.如图,在平面直角坐标系中,两条曲线关于原点O成中心对称,过点O作一条直线分别与两条曲线交于点E、F,该直线将曲线与坐标轴围成的封闭图形分成四部分.若阴影部分①的面积是3,阴影部分④的面积是2,则图中两条曲线与坐标轴围成的封闭图形的面积之和是 .
12.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,△B2A2B1与△OA1B1关于点B1成中心对称,△B2A3B3与△B2A2B1关于点B2成中心对称,……,按照这个规律,△B2 020A2 021B2 021的顶点A2 021的坐标是 .
三、解答题
13.如图,△ABC与△DEF关于点O成中心对称,请你写出这两个三角形中的对称点、相等的线段、相等的角.
14.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
15.如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)△A1B1C1与△ABC关于点(1,2)成中心对称,画出△A1B1C1,平移△ABC,若点A平移后的对应点A2的坐标为(-1,-4),画出平移后得到的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
答案全解全析
一、选择题
1.答案 C 根据中心对称的概念,知(2)(3)(4)都成中心对称.故选C.
2.答案 D 选项A,△ABC与△A'B'C'关于y轴对称,故选项A不符合题意;选项B,△ABC与△A'B'C'关于x轴对称,故选项B不符合题意;选项C,△ABC与△A'B'C'关于点成中心对称,故选项C不符合题意;选项D,△ABC与△A'B'C'关于原点成中心对称,故选项D符合题意.故选D.
3.答案 D 选项A中,∵AD与EF关于点O成中心对称,∴AD∥EF,同理可得AB∥GF,所以说法正确;选项B中,∵B与G关于点O成中心对称,∴BO=GO,所以说法正确;选项C中,∵CD与HE关于点O成中心对称,∴CD=HE,同理可得BC=GH,所以说法正确;选项D中,根据题中条件无法证明DO=HO,故说法错误.故选D.
4.答案 D △ABC与△CDA关于点O成中心对称,则AB=CD,AD=BC,所以四边形ABCD是平行四边形,可知:①点E和点F,点B和点D是对称点,正确;②直线BD必经过点O,正确;③四边形DEOC与四边形BFOA的面积必相等,正确;④△AOE与△COF成中心对称,正确,故正确的个数为4.故选D.
5. 答案 B ∵△ABC与△A'B'C'关于点O成中心对称,
∴OC=OC',BC∥B'C',点B的对称点是点B',故A,C,D正确.故选B.
二、填空题
6.答案 点C;点F;点D;EG;EG;点C;△FGE
解析 四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是点C,点A的对称点是点F,点E的对称点是点D.BD∥EG且BD=EG.连接A,F的线段经过点C,△ABD≌△FGE.
7.答案 ∠AOB=90°(答案不唯一)
解析 ∵△AOB与△COD关于公共顶点O成中心对称,∴点A、O、C在一条直线上,点B、O、D在一条直线上,且AO=OC,BO=DO,∴四边形ABCD是平行四边形.当∠AOB=90°时,平行四边形ABCD是菱形,答案不唯一.
8.答案
解析 ∵△DEC 与△ABC关于点C成中心对称,∴DC=AC=1,DE=AB=3,∴在Rt△EDA中,AE==.∵点F是DE的中点,AC=DC,∴CF是△ADE的中位线,∴CF=AE=.
9.答案 48
解析 ∵四边形ABCD是矩形,∴∠B=90°.
∵AB=3,BC=4,∴AC===5,∴△ABC的周长=3+4+5=12.
∵矩形ABCD和矩形A'B'C'D关于点D成中心对称,∴阴影部分的四个直角三角形全等,∴阴影部分的周长和=4×12=48.
10. 答案 15
解析 如图,作AE⊥b于点E,由题可知,四边形ABOE为矩形,图形①与图形②的面积相等,AB=OD=3,∴阴影部分的面积=矩形ABOE的面积=3×5=15.
11. 答案 10
解析 两条曲线关于点O成中心对称,则阴影部分①和③关于点O成中心对称,阴影部分②和④关于点O成中心对称,∴封闭图形的面积之和是(2+3)×2=10.
12. 答案 (4 041,)
解析 ∵△OA1B1是边长为2的等边三角形,∴A1的坐标为(1,),B1的坐标为(2,0).∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∴点A2的坐标是(3,-).同理可得,点A3的坐标是(5,),点A4的坐标是
(7,-),……,∵1=2×1-1,3=2×2-1,5=2×3-1,7=2×4-1,……,∴点An的横坐标是2n-1,又∵当n为奇数时,点An的纵坐标是,当n为偶数时,点An的纵坐标是
-,∴△B2 020A2 021B2 021的顶点A2 021的横坐标是2×2 021-1=4 041,纵坐标是.
三、解答题
13.解析 对称点:A和D,B和E,C和F;
相等的线段:AC=DF,AB=DE,BC=EF;
相等的角:∠CAB=∠FDE,∠ABC=∠DEF,∠BCA=∠EFD.
14.解析 (1)根据中心对称的性质,可得对称中心是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是4-2=2,
∴B,C的坐标分别是(-2,4),(-2,2).
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3).
综上可得,顶点B,C,B1,C1的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
15.解析 (1)△A1B1C1如图所示,△A2B2C2如图所示.
(2)旋转中心的坐标为(2,-1).
同课章节目录
