2022-2023学年人教版九年级数学上册23.2.2中心对称图形 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册23.2.2中心对称图形 章节培优训练试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 381.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 08:48:08 | ||
图片预览




文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十三章 旋转
23.2 中心对称
23.2.2 中心对称图形
一、选择题
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
2. 观察如图所示的脸谱图案,下列说法正确的是( )
A.它是轴对称图形,不是中心对称图形
B.它是中心对称图形,不是轴对称图形
C.它既是轴对称图形,也是中心对称图形
D.它既不是轴对称图形,也不是中心对称图形
3.下列函数图象中,既是中心对称图形又是轴对称图形的是( )
A B C D
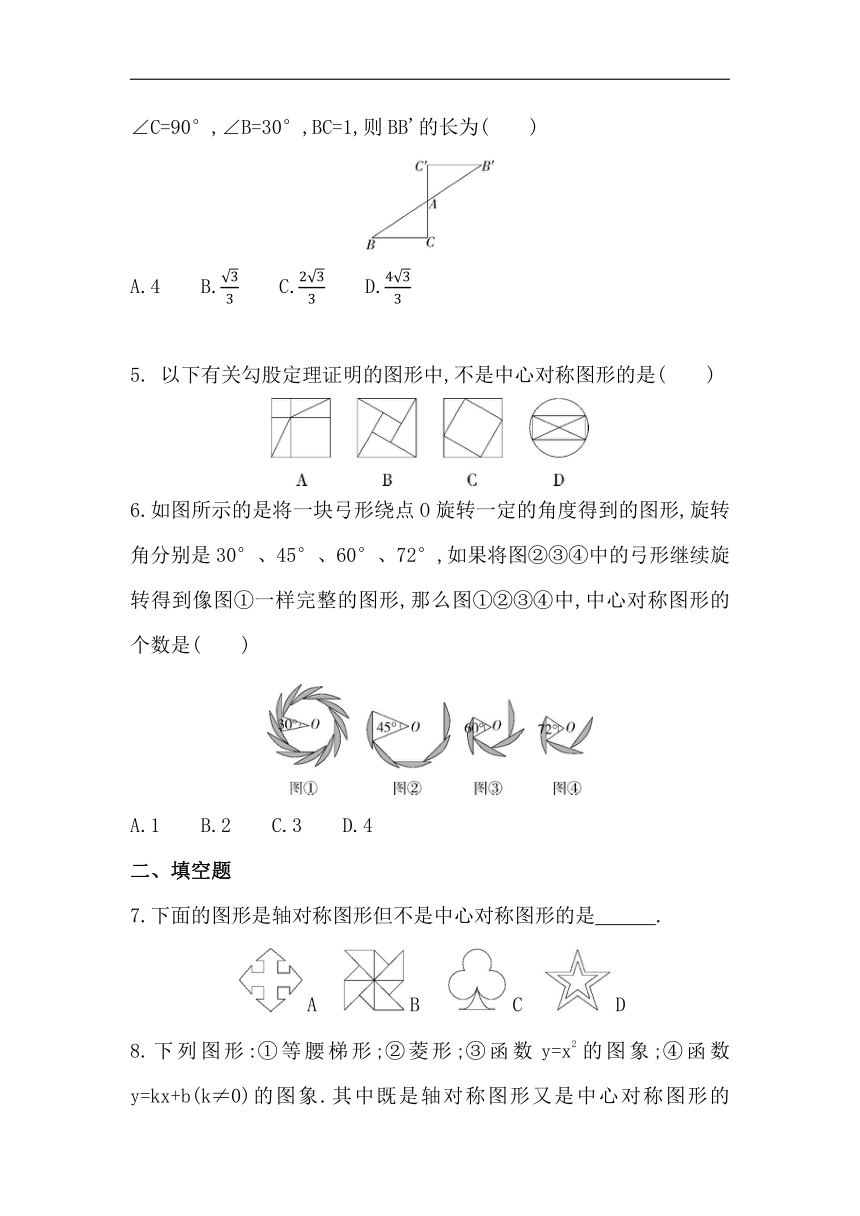
4.如图所示的是一个中心对称图形,点A为对称中心,若∠C=90°,∠B=30°,BC=1,则BB'的长为( )
A.4 B. C. D.
5. 以下有关勾股定理证明的图形中,不是中心对称图形的是( )
6.如图所示的是将一块弓形绕点O旋转一定的角度得到的图形,旋转角分别是30°、45°、60°、72°,如果将图②③④中的弓形继续旋转得到像图①一样完整的图形,那么图①②③④中,中心对称图形的个数是( )
A.1 B.2 C.3 D.4
二、填空题
7.下面的图形是轴对称图形但不是中心对称图形的是 .
A B C D
8.下列图形:①等腰梯形;②菱形;③函数y=x2的图象;④函数y=kx+b(k≠0)的图象.其中既是轴对称图形又是中心对称图形的是 .(填序号)
9.有下列平面图形:线段、等腰直角三角形、等边三角形、平行四边形、长方形、正方形、圆,其中轴对称图形有a个,中心对称图形有b个,则a2+b3的值为 .
10.在一次数学社团活动中,小明设计了一个社团标识,如图所示,正方形ABCD与折线DE—EF—FB构成了一个中心对称图形,且DE⊥EF,AD=50,DE比EF长25,那么EF的长是 .
三、解答题
11.(1)写出两个既是轴对称图形又是中心对称图形的图形;
(2)写出两个是轴对称图形而不是中心对称图形的图形;
(3)写出两个不是轴对称图形而是中心对称图形的图形.
12.如图,△ABC中,D是BC上一点,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E、F关于直线AD对称.
13.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画出一个三角形,使它的三边长都是无理数,并通过旋转或轴对称作出一个中心对称图形;
(2)在图2中,画出一个直角三角形,使它的三边长都是整数,并通过旋转或轴对称作出一个中心对称图形;
(3)在图3中,画出一个中心对称图形.
答案全解全析
一、选择题
1.答案 B 选项A中图形是轴对称图形,不是中心对称图形;选项B中图形既是轴对称图形,又是中心对称图形;选项C中图形不是轴对称图形,是中心对称图形;选项D中图形是轴对称图形,不是中心对称图形.故选B.
2.答案 A 该图案是轴对称图形,不是中心对称图形.故选A.
3.答案 A 选项A中函数图象既是中心对称图形又是轴对称图形,符合题意;
选项B中函数图象是轴对称图形,但不是中心对称图形,不符合题意;
选项C中函数图象是轴对称图形,但不是中心对称图形,不符合题意;
选项D中函数图象不是轴对称图形,是中心对称图形,不符合题意.故选A.
4. 答案 D ∵∠C=90°,∠B=30°,∴AB=2AC.∵BC=1,∴由勾股定理可得AB=,又题图为一个中心对称图形,点A为对称中心,∴BB'=2AB=.故选D.
5. 答案 A 选项A中的图形是轴对称图形,不是中心对称图形;选项B、C中的图形是中心对称图形,不是轴对称图形;选项D中的图形既是中心对称图形,又是轴对称图形.
6. 答案 C 得到的完整图形中,图①由12个弓形组成,图②由8个弓形组成,图③由6个弓形组成,图④由5个弓形组成,所以图①②③是中心对称图形,图④不是中心对称图形.故选C.
二、填空题
7.答案 C,D
解析 A中图形既是轴对称图形,又是中心对称图形;B中图形不是轴对称图形,是中心对称图形;C中图形是轴对称图形,不是中心对称图形;D中图形是轴对称图形,不是中心对称图形.
8.答案 ②④
解析 ①等腰梯形是轴对称图形,不是中心对称图形;②菱形既是轴对称图形又是中心对称图形;③函数y=x2的图象是轴对称图形,不是中心对称图形;④函数y=kx+b(k≠0)的图象既是轴对称图形又是中心对称图形.所以,既是轴对称图形又是中心对称图形的为②④.
9. 答案 161
解析 轴对称图形:线段、等腰直角三角形、等边三角形、长方形、正方形、圆,共6个,∴a=6;
中心对称图形:线段、平行四边形、长方形、正方形、圆,共5个,
∴b=5.∴a2+b3=62+53=161.
10. 答案 10
解析 如图,连接BD,与EF交于点O,
∵正方形ABCD与折线DE—EF—FB构成了中心对称图形,
∴OE=EF,OD=BD,∵AD=50,
∴BD==50,
∴OD=25.设EF=2x,则OE=x,DE=2x+25,在Rt△DOE中,
x2+(2x+25)2=(25)2,解得x=5或x=-25(舍去),
∴EF=5×2=10.
三、解答题
11.解析 答案不唯一.(1)既是轴对称图形又是中心对称图形的图形:正方形、菱形.
(2)是轴对称图形而不是中心对称图形的图形:等腰梯形、等腰三角形.
(3)不是轴对称图形而是中心对称图形的图形:一般的平行四边形(非矩形、菱形、正方形)、太极图(不考虑颜色).
12.解析 (1)证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴四边形AEDF是中心对称图形.
(2)∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE.
又∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,
连接EF,则AD垂直平分EF,
∴点E、F关于直线AD对称.
13.解析 (1)答案不唯一,如三边长分别为2、、,如图1.
(2)三边长分别为3、4、5,如图2.
(3)答案不唯一,如画一个平行四边形,如图3.
班级 姓名
第二十三章 旋转
23.2 中心对称
23.2.2 中心对称图形
一、选择题
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A B C D
2. 观察如图所示的脸谱图案,下列说法正确的是( )
A.它是轴对称图形,不是中心对称图形
B.它是中心对称图形,不是轴对称图形
C.它既是轴对称图形,也是中心对称图形
D.它既不是轴对称图形,也不是中心对称图形
3.下列函数图象中,既是中心对称图形又是轴对称图形的是( )
A B C D
4.如图所示的是一个中心对称图形,点A为对称中心,若∠C=90°,∠B=30°,BC=1,则BB'的长为( )
A.4 B. C. D.
5. 以下有关勾股定理证明的图形中,不是中心对称图形的是( )
6.如图所示的是将一块弓形绕点O旋转一定的角度得到的图形,旋转角分别是30°、45°、60°、72°,如果将图②③④中的弓形继续旋转得到像图①一样完整的图形,那么图①②③④中,中心对称图形的个数是( )
A.1 B.2 C.3 D.4
二、填空题
7.下面的图形是轴对称图形但不是中心对称图形的是 .
A B C D
8.下列图形:①等腰梯形;②菱形;③函数y=x2的图象;④函数y=kx+b(k≠0)的图象.其中既是轴对称图形又是中心对称图形的是 .(填序号)
9.有下列平面图形:线段、等腰直角三角形、等边三角形、平行四边形、长方形、正方形、圆,其中轴对称图形有a个,中心对称图形有b个,则a2+b3的值为 .
10.在一次数学社团活动中,小明设计了一个社团标识,如图所示,正方形ABCD与折线DE—EF—FB构成了一个中心对称图形,且DE⊥EF,AD=50,DE比EF长25,那么EF的长是 .
三、解答题
11.(1)写出两个既是轴对称图形又是中心对称图形的图形;
(2)写出两个是轴对称图形而不是中心对称图形的图形;
(3)写出两个不是轴对称图形而是中心对称图形的图形.
12.如图,△ABC中,D是BC上一点,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E、F关于直线AD对称.
13.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画出一个三角形,使它的三边长都是无理数,并通过旋转或轴对称作出一个中心对称图形;
(2)在图2中,画出一个直角三角形,使它的三边长都是整数,并通过旋转或轴对称作出一个中心对称图形;
(3)在图3中,画出一个中心对称图形.
答案全解全析
一、选择题
1.答案 B 选项A中图形是轴对称图形,不是中心对称图形;选项B中图形既是轴对称图形,又是中心对称图形;选项C中图形不是轴对称图形,是中心对称图形;选项D中图形是轴对称图形,不是中心对称图形.故选B.
2.答案 A 该图案是轴对称图形,不是中心对称图形.故选A.
3.答案 A 选项A中函数图象既是中心对称图形又是轴对称图形,符合题意;
选项B中函数图象是轴对称图形,但不是中心对称图形,不符合题意;
选项C中函数图象是轴对称图形,但不是中心对称图形,不符合题意;
选项D中函数图象不是轴对称图形,是中心对称图形,不符合题意.故选A.
4. 答案 D ∵∠C=90°,∠B=30°,∴AB=2AC.∵BC=1,∴由勾股定理可得AB=,又题图为一个中心对称图形,点A为对称中心,∴BB'=2AB=.故选D.
5. 答案 A 选项A中的图形是轴对称图形,不是中心对称图形;选项B、C中的图形是中心对称图形,不是轴对称图形;选项D中的图形既是中心对称图形,又是轴对称图形.
6. 答案 C 得到的完整图形中,图①由12个弓形组成,图②由8个弓形组成,图③由6个弓形组成,图④由5个弓形组成,所以图①②③是中心对称图形,图④不是中心对称图形.故选C.
二、填空题
7.答案 C,D
解析 A中图形既是轴对称图形,又是中心对称图形;B中图形不是轴对称图形,是中心对称图形;C中图形是轴对称图形,不是中心对称图形;D中图形是轴对称图形,不是中心对称图形.
8.答案 ②④
解析 ①等腰梯形是轴对称图形,不是中心对称图形;②菱形既是轴对称图形又是中心对称图形;③函数y=x2的图象是轴对称图形,不是中心对称图形;④函数y=kx+b(k≠0)的图象既是轴对称图形又是中心对称图形.所以,既是轴对称图形又是中心对称图形的为②④.
9. 答案 161
解析 轴对称图形:线段、等腰直角三角形、等边三角形、长方形、正方形、圆,共6个,∴a=6;
中心对称图形:线段、平行四边形、长方形、正方形、圆,共5个,
∴b=5.∴a2+b3=62+53=161.
10. 答案 10
解析 如图,连接BD,与EF交于点O,
∵正方形ABCD与折线DE—EF—FB构成了中心对称图形,
∴OE=EF,OD=BD,∵AD=50,
∴BD==50,
∴OD=25.设EF=2x,则OE=x,DE=2x+25,在Rt△DOE中,
x2+(2x+25)2=(25)2,解得x=5或x=-25(舍去),
∴EF=5×2=10.
三、解答题
11.解析 答案不唯一.(1)既是轴对称图形又是中心对称图形的图形:正方形、菱形.
(2)是轴对称图形而不是中心对称图形的图形:等腰梯形、等腰三角形.
(3)不是轴对称图形而是中心对称图形的图形:一般的平行四边形(非矩形、菱形、正方形)、太极图(不考虑颜色).
12.解析 (1)证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴四边形AEDF是中心对称图形.
(2)∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE.
又∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,
连接EF,则AD垂直平分EF,
∴点E、F关于直线AD对称.
13.解析 (1)答案不唯一,如三边长分别为2、、,如图1.
(2)三边长分别为3、4、5,如图2.
(3)答案不唯一,如画一个平行四边形,如图3.
同课章节目录
