2022-2023学年 人教版 九年级数学上册23.2.3关于原点对称的点的坐标 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年 人教版 九年级数学上册23.2.3关于原点对称的点的坐标 章节培优训练试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 185.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 08:50:39 | ||
图片预览


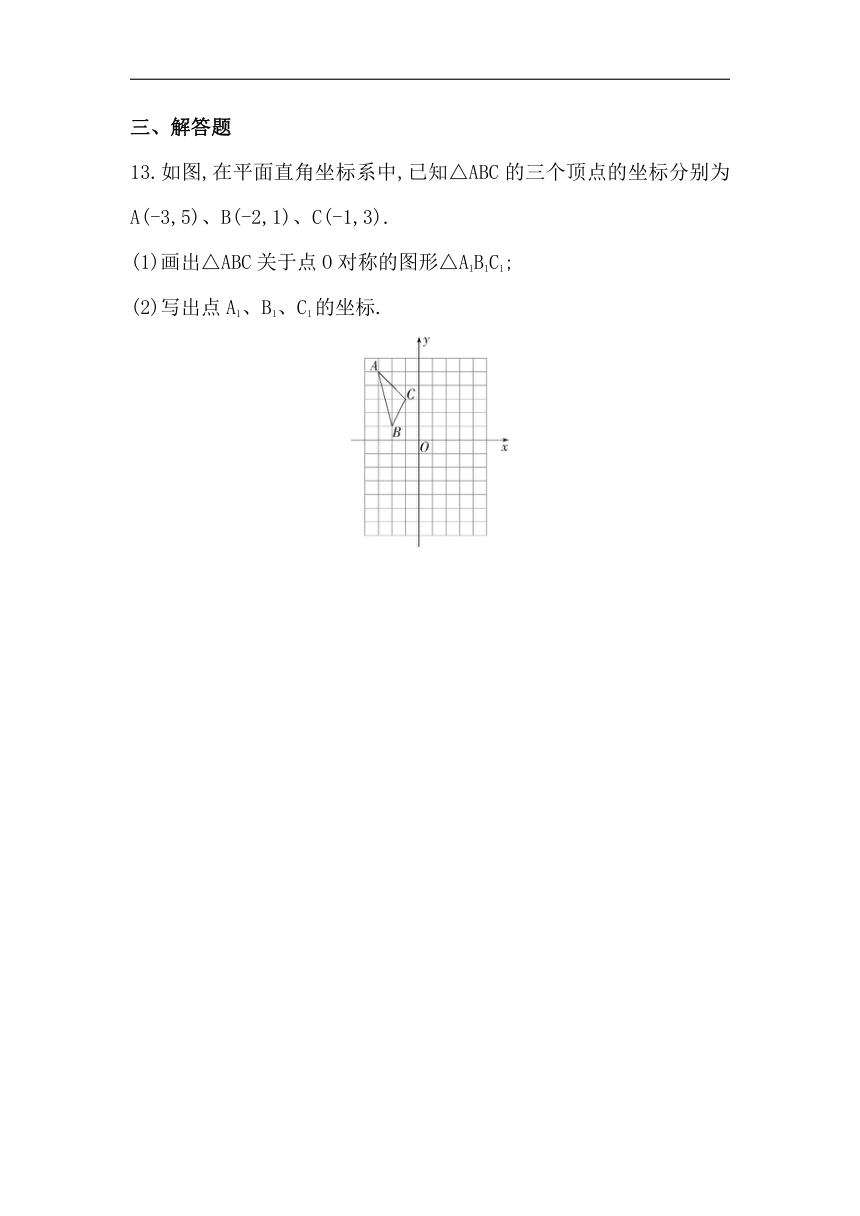

文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十三章 旋转
23.2 中心对称
23.2.3 关于原点对称的点的坐标
一、选择题
1. 平面直角坐标系中点P(7,-9)关于原点对称的点的坐标是( )
A.(-9,7) B.(-7,9) C.(7,9) D.(-7,-9)
2. 在平面直角坐标系中,已知点A(m,3)与点B(-1,n)关于原点对称,则m+n的值为( )
A.4 B.-4 C.-2 D.2
3. 若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是( )
A.1 B.3 C.5 D.7
4. 若点P(a+1,a-2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是( )
A B C D
5.在平面直角坐标系中,若点P(x,y)在第四象限,且|x|-2=0,y2-9=0,则点P关于原点对称的点P'的坐标是( )
A.(2,-3) B.(-3,2) C.(-2,3) D.(-2,-3)
6.已知点(-a,a)(其中a>0),给出下列变换:①先关于x轴作轴对称变换,再关于y轴作轴对称变换;②先关于y轴作轴对称变换,再关于x轴作轴对称变换;③关于原点作中心对称变换;④关于直线y=x作轴对称变换;⑤沿直线y=-x向右下平移2a个单位.其中能使得到的对应点的坐标为(a,-a)的变换的个数是( )
A.2 B.3 C.4 D.5
7.以下每对函数的图象一定关于原点对称的是( )
A.y=x2与y=-2x2
B.y=x2+1与y=-x2
C.y=x2+1与y=-x2-1
D.y=(x-1)2与y=(x+1)2
二、填空题
8.若点A(-m,n-5)与点B(-1,-2m)关于原点对称,则-mn= .
9.在平面直角坐标系xOy中,如果有点P(-1,2)与点Q(1,-2),那么:①点P与点Q关于x轴对称;②点P与点Q关于y轴对称;③点P与点Q关于原点对称;④点P与点Q都在y=-2x的图象上.前面的四种描述正确的是 .(填序号)
10.在平面直角坐标系中,将点P(-1,-2)向右平移3个单位长度得到点P1,则点P1关于原点的对称点P2的坐标是 .
11.若点M(-3,y)与点N(x,y-1)关于原点对称,则yx的值为 .
12.在平面直角坐标系中,点A(x2,-3)与点B(2x,3)关于原点对称,则点A的坐标为 .
三、解答题
13.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5)、B(-2,1)、C(-1,3).
(1)画出△ABC关于点O对称的图形△A1B1C1;
(2)写出点A1、B1、C1的坐标.
14.如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.
(1)请分别写出点A与点M,点B与点N,点C与点Q的坐标;
(2)已知点P是三角形ABC内一点,其坐标为(-3,2),写出三角形MNQ中的对应点R的坐标.
答案全解全析
一、选择题
1.答案 B 点P(7,-9)关于原点对称的点的坐标是(-7,9).故选B.
2.答案 C ∵点A(m,3)与点B(-1,n)关于原点对称,∴m=1,n=-3,∴m+n=1-3=-2.故选C.
3.答案 C ∵点P(m-1,5)与点Q(3,2-n)关于原点对称,∴m-1=-3,2-n=-5,解得m=-2,n=7,则m+n=-2+7=5.故选C.
4.答案 C ∵点P(a+1,a-2)关于原点对称的点在第二象限,∴点P在第四象限,∴a+1>0,a-2<0,解得-15. 答案 C
∵点P(x,y)在第四象限,
∴x>0,y<0,
∵|x|-2=0,y2-9=0,
∴x=2,y=-3,
∴P(2,-3),其关于原点对称的点P'的坐标是(-2,3).
6. 答案 D 点(-a,a)关于x轴对称的点是(-a,-a),点(-a,-a)关于y轴对称的点是(a,-a),则①符合要求;同理,②符合要求;点(-a,a)关于原点中心对称的点是(a,-a),则③符合要求;点(-a,a)和(a,-a)都在直线y=-x上,直线y=-x与直线y=x互相垂直,垂足为O,且两点到原点O的距离都是a,所以点(-a,a)关于直线y=x对称的点为(a,-a),故④符合要求;由④可知,⑤符合要求.故选D.
7. 答案 C 选项A中,两函数图象开口方向相反,但开口大小不同,所以两函数图象不关于原点对称;选项B中,函数y=x2+1的图象的顶点坐标为(0,1),函数y=-x2的图象的顶点坐标为(0,0),两个顶点不关于原点对称,所以两函数图象不关于原点对称;选项C中,函数y=x2+1的图象开口向上,顶点坐标为(0,1),函数y=-x2-1的图象开口向下,顶点坐标为(0,-1),点(0,1)和点(0,-1)关于原点对称,同时两函数图象开口方向相反,且开口大小相同,所以两函数图象关于原点对称;选项D中,两函数图象开口方向都向上,所以两函数图象不关于原点对称.故选C.
二、填空题
8.答案 1
解析 ∵点A(-m,n-5)与点B(-1,-2m)关于原点对称,∴-m=1,n-5=2m,
∴m=-1,n=3.
∴-mn=-(-1)3=1.
9.答案 ③④
解析 如图所示,点P与点Q关于原点对称,③正确.∵对于y=-2x,当x=-1时,y=2;当x=1时,y=-2,∴点P与点Q都在y=-2x的图象上,④正确.显然①②错误.
10. 答案 (-2,2)
解析 将点P(-1,-2)向右平移3个单位长度得到点P1(2,-2),则点P1关于原点的对称点P2的坐标是(-2,2).
11. 答案
解析 ∵点M(-3,y)与点N(x,y-1)关于原点对称,
∴x=3,y-1=-y,解得x=3,y=,
∴yx的值为.
12. 答案 (0,-3)或(4,-3)
解析 ∵点A(x2,-3)与点B(2x,3)关于原点对称,
∴x2=-2x,
∴x2+2x=0,
∴x(x+2)=0,解得x1=0,x2=-2,
∴x2=0或x2=4,
∴点A的坐标为(0,-3)或(4,-3).
三、解答题
13.解析 (1)如图,△A1B1C1即为所求.
(2)A1(3,-5),B1(2,-1),C1(1,-3).
14.解析 (1)A(-4,1),M(4,-1);
B(-1,2),N(1,-2);
C(-3,4),Q(3,-4).
(2)三角形MNQ中的点R的坐标为(3,-2).
班级 姓名
第二十三章 旋转
23.2 中心对称
23.2.3 关于原点对称的点的坐标
一、选择题
1. 平面直角坐标系中点P(7,-9)关于原点对称的点的坐标是( )
A.(-9,7) B.(-7,9) C.(7,9) D.(-7,-9)
2. 在平面直角坐标系中,已知点A(m,3)与点B(-1,n)关于原点对称,则m+n的值为( )
A.4 B.-4 C.-2 D.2
3. 若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是( )
A.1 B.3 C.5 D.7
4. 若点P(a+1,a-2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是( )
A B C D
5.在平面直角坐标系中,若点P(x,y)在第四象限,且|x|-2=0,y2-9=0,则点P关于原点对称的点P'的坐标是( )
A.(2,-3) B.(-3,2) C.(-2,3) D.(-2,-3)
6.已知点(-a,a)(其中a>0),给出下列变换:①先关于x轴作轴对称变换,再关于y轴作轴对称变换;②先关于y轴作轴对称变换,再关于x轴作轴对称变换;③关于原点作中心对称变换;④关于直线y=x作轴对称变换;⑤沿直线y=-x向右下平移2a个单位.其中能使得到的对应点的坐标为(a,-a)的变换的个数是( )
A.2 B.3 C.4 D.5
7.以下每对函数的图象一定关于原点对称的是( )
A.y=x2与y=-2x2
B.y=x2+1与y=-x2
C.y=x2+1与y=-x2-1
D.y=(x-1)2与y=(x+1)2
二、填空题
8.若点A(-m,n-5)与点B(-1,-2m)关于原点对称,则-mn= .
9.在平面直角坐标系xOy中,如果有点P(-1,2)与点Q(1,-2),那么:①点P与点Q关于x轴对称;②点P与点Q关于y轴对称;③点P与点Q关于原点对称;④点P与点Q都在y=-2x的图象上.前面的四种描述正确的是 .(填序号)
10.在平面直角坐标系中,将点P(-1,-2)向右平移3个单位长度得到点P1,则点P1关于原点的对称点P2的坐标是 .
11.若点M(-3,y)与点N(x,y-1)关于原点对称,则yx的值为 .
12.在平面直角坐标系中,点A(x2,-3)与点B(2x,3)关于原点对称,则点A的坐标为 .
三、解答题
13.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5)、B(-2,1)、C(-1,3).
(1)画出△ABC关于点O对称的图形△A1B1C1;
(2)写出点A1、B1、C1的坐标.
14.如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经过某种变换后得到的图形.
(1)请分别写出点A与点M,点B与点N,点C与点Q的坐标;
(2)已知点P是三角形ABC内一点,其坐标为(-3,2),写出三角形MNQ中的对应点R的坐标.
答案全解全析
一、选择题
1.答案 B 点P(7,-9)关于原点对称的点的坐标是(-7,9).故选B.
2.答案 C ∵点A(m,3)与点B(-1,n)关于原点对称,∴m=1,n=-3,∴m+n=1-3=-2.故选C.
3.答案 C ∵点P(m-1,5)与点Q(3,2-n)关于原点对称,∴m-1=-3,2-n=-5,解得m=-2,n=7,则m+n=-2+7=5.故选C.
4.答案 C ∵点P(a+1,a-2)关于原点对称的点在第二象限,∴点P在第四象限,∴a+1>0,a-2<0,解得-1
∵点P(x,y)在第四象限,
∴x>0,y<0,
∵|x|-2=0,y2-9=0,
∴x=2,y=-3,
∴P(2,-3),其关于原点对称的点P'的坐标是(-2,3).
6. 答案 D 点(-a,a)关于x轴对称的点是(-a,-a),点(-a,-a)关于y轴对称的点是(a,-a),则①符合要求;同理,②符合要求;点(-a,a)关于原点中心对称的点是(a,-a),则③符合要求;点(-a,a)和(a,-a)都在直线y=-x上,直线y=-x与直线y=x互相垂直,垂足为O,且两点到原点O的距离都是a,所以点(-a,a)关于直线y=x对称的点为(a,-a),故④符合要求;由④可知,⑤符合要求.故选D.
7. 答案 C 选项A中,两函数图象开口方向相反,但开口大小不同,所以两函数图象不关于原点对称;选项B中,函数y=x2+1的图象的顶点坐标为(0,1),函数y=-x2的图象的顶点坐标为(0,0),两个顶点不关于原点对称,所以两函数图象不关于原点对称;选项C中,函数y=x2+1的图象开口向上,顶点坐标为(0,1),函数y=-x2-1的图象开口向下,顶点坐标为(0,-1),点(0,1)和点(0,-1)关于原点对称,同时两函数图象开口方向相反,且开口大小相同,所以两函数图象关于原点对称;选项D中,两函数图象开口方向都向上,所以两函数图象不关于原点对称.故选C.
二、填空题
8.答案 1
解析 ∵点A(-m,n-5)与点B(-1,-2m)关于原点对称,∴-m=1,n-5=2m,
∴m=-1,n=3.
∴-mn=-(-1)3=1.
9.答案 ③④
解析 如图所示,点P与点Q关于原点对称,③正确.∵对于y=-2x,当x=-1时,y=2;当x=1时,y=-2,∴点P与点Q都在y=-2x的图象上,④正确.显然①②错误.
10. 答案 (-2,2)
解析 将点P(-1,-2)向右平移3个单位长度得到点P1(2,-2),则点P1关于原点的对称点P2的坐标是(-2,2).
11. 答案
解析 ∵点M(-3,y)与点N(x,y-1)关于原点对称,
∴x=3,y-1=-y,解得x=3,y=,
∴yx的值为.
12. 答案 (0,-3)或(4,-3)
解析 ∵点A(x2,-3)与点B(2x,3)关于原点对称,
∴x2=-2x,
∴x2+2x=0,
∴x(x+2)=0,解得x1=0,x2=-2,
∴x2=0或x2=4,
∴点A的坐标为(0,-3)或(4,-3).
三、解答题
13.解析 (1)如图,△A1B1C1即为所求.
(2)A1(3,-5),B1(2,-1),C1(1,-3).
14.解析 (1)A(-4,1),M(4,-1);
B(-1,2),N(1,-2);
C(-3,4),Q(3,-4).
(2)三角形MNQ中的点R的坐标为(3,-2).
同课章节目录
