2022-2023学年人教版九年级数学上册24.1.1 圆 章节培优训练试卷 (含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册24.1.1 圆 章节培优训练试卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 261.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 00:00:00 | ||
图片预览


文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.1 圆
一、选择题
1. 小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定错误的是( )
A.4 B.5 C.10 D.11
2. 下列说法中,正确的是( )
A.两个半圆是等弧 B.同圆中优弧与半圆的差必是劣弧
C.长度相等的弧是等弧 D.同圆中优弧与劣弧的差必是优弧
3.如图所示,点M是☉O上的任意一点,下列结论:
①以M为端点的弦只有一条;②以M为端点的半径只有一条;③以M为端点的直径只有一条;④以M为端点的弧只有一条.
其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,OA是☉O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交☉O于点C.以OB、BC为边作矩形OBCD,连接BD.若CD=6,BC=8,则AB的长为( )
A.6 B.5 C.4 D.2
5.如图,BC是☉O的直径,AB是☉O的弦,若∠AOC=60°,则∠OAB的度数是( )
A.20° B.25°
C.30° D.35°
6.下列说法:①直径是最长的弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半径相等的两个圆是等圆,其中说法正确的有( )
A.1个 B.2个
C.3个 D.4个
7.如图,AB,CD是☉O的两条相互垂直的直径,点E是☉O上的动点,过点E作EF⊥AB于F,EG⊥CD于G,连接FG,FG的中点为P.若点E在圆周上运动一周,下列结论错误的是( )
A.FG的长不变
B.点P到点O的距离不变
C.点P到点E的距离不变
D.点P到AB、CD的距离不变
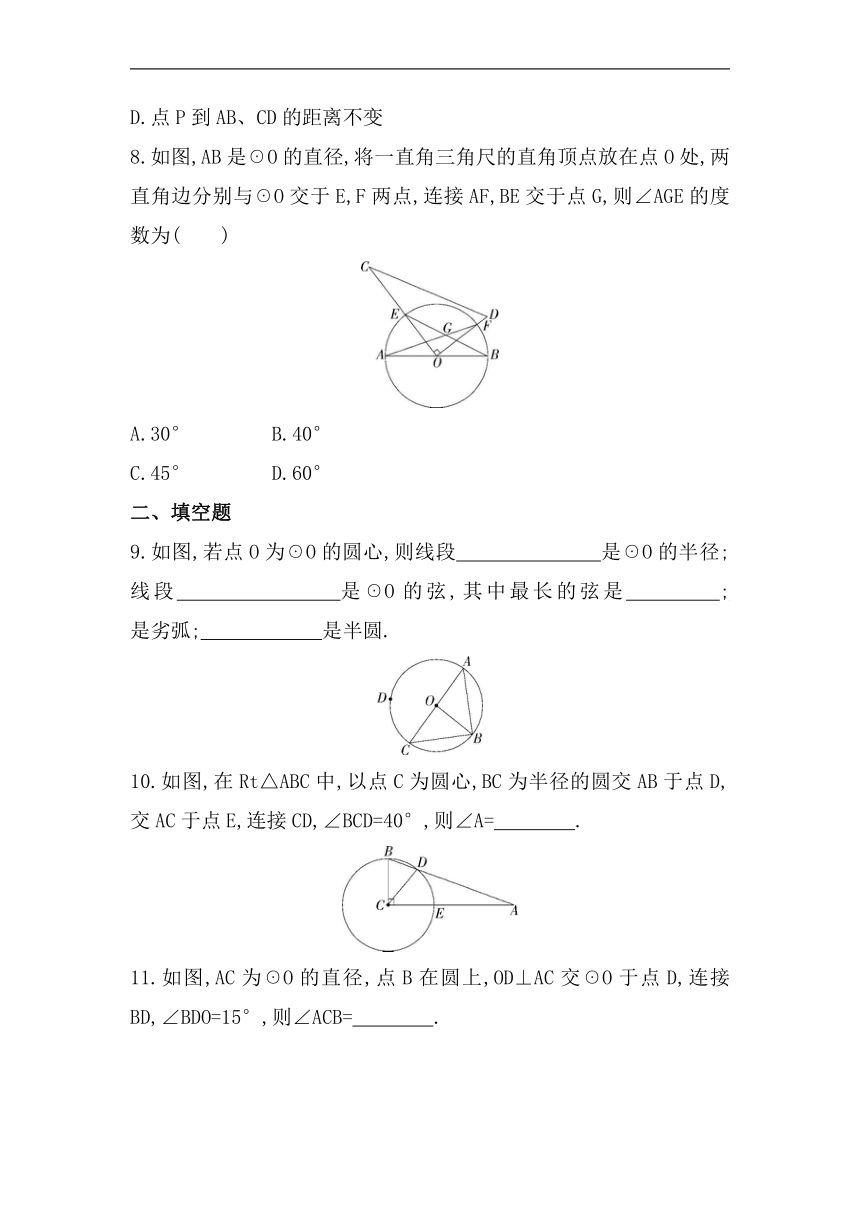
8.如图,AB是☉O的直径,将一直角三角尺的直角顶点放在点O处,两直角边分别与☉O交于E,F两点,连接AF,BE交于点G,则∠AGE的度数为( )
A.30° B.40°
C.45° D.60°
二、填空题
9.如图,若点O为☉O的圆心,则线段 是☉O的半径;线段 是☉O的弦,其中最长的弦是 ; 是劣弧; 是半圆.
10.如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,连接CD,∠BCD=40°,则∠A= .
11.如图,AC为☉O的直径,点B在圆上,OD⊥AC交☉O于点D,连接BD,∠BDO=15°,则∠ACB= .
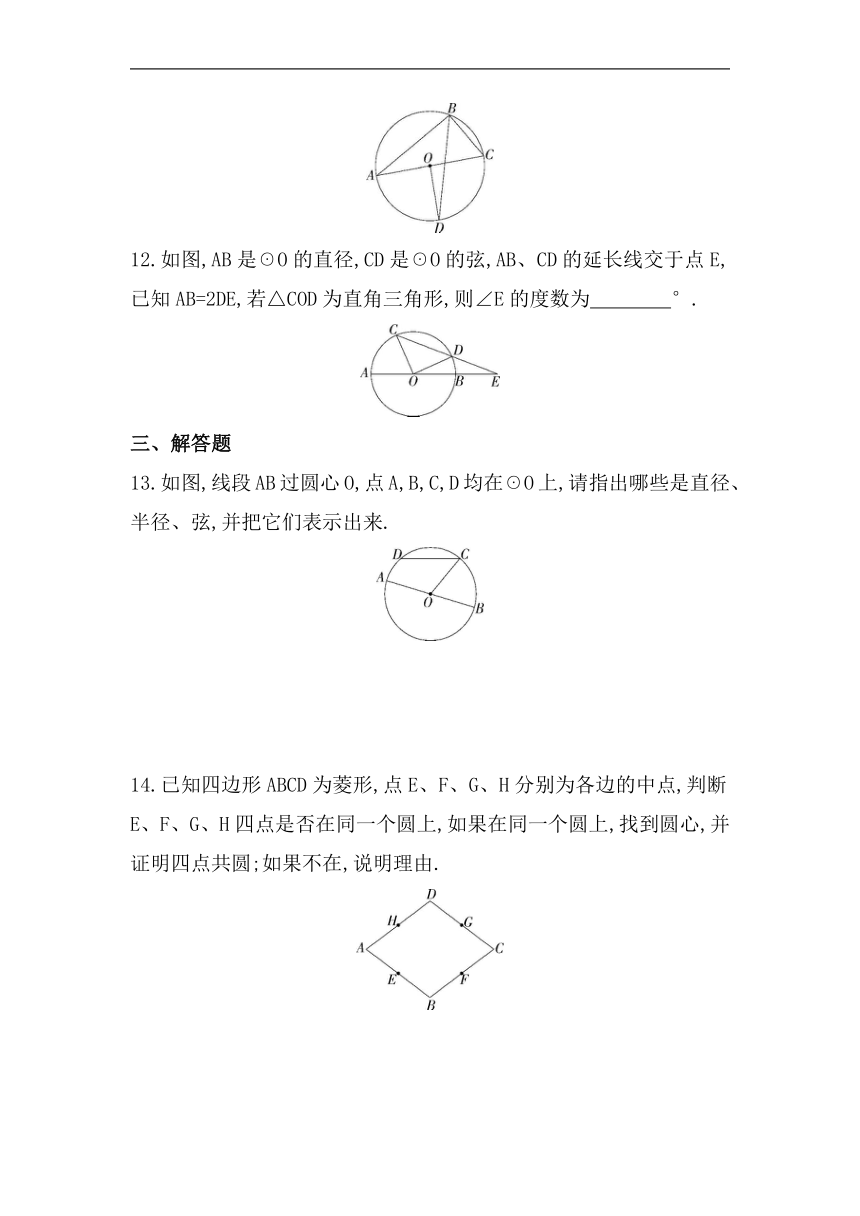
12.如图,AB是☉O的直径,CD是☉O的弦,AB、CD的延长线交于点E,已知AB=2DE,若△COD为直角三角形,则∠E的度数为 °.
三、解答题
13.如图,线段AB过圆心O,点A,B,C,D均在☉O上,请指出哪些是直径、半径、弦,并把它们表示出来.
14.已知四边形ABCD为菱形,点E、F、G、H分别为各边的中点,判断E、F、G、H四点是否在同一个圆上,如果在同一个圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
答案全解全析
一、选择题
1.答案 D ∵半径为5的圆的直径为10,∴在半径为5的圆中测量弦AB的长度,AB的取值范围是02.答案 B 选项A,两个半圆的半径不一定相等,故A中说法错误;选项B,同圆中优弧与半圆的差必是劣弧,故B中说法正确;选项C,长度相等的弧半径不一定相等,所以不一定是等弧,故C中说法错误;选项D,同圆中优弧与劣弧的差可能是劣弧,故D中说法错误.故选B.
3.答案 B 以M为端点的弦有无数条,所以①中结论错误;②正确;③正确;以M为端点的弧有无数条,所以④中结论错误.故选B.
4.答案 C 如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,OB=CD=6,BC=8,
∴OA=OC==10,∴AB=OA-OB=4.故选C.
5. 答案 C ∵∠AOC=60°,∴∠BOA=180°-60°=120°,
∵OA=OB,
∴∠OAB=∠B==30°.
6. 答案 C ①直径是最长的弦,正确;②过圆心的弦才是直径,故原说法错误;③半径相等的两个半圆是等弧,正确;④长度相等的两条弧不一定是等弧,故原说法错误;⑤半径相等的两个圆是等圆,正确.
7. 答案 D 由题意知,四边形OFEG是矩形,连接OE,则OE=FG,点P为OE与FG的交点,OP=EP=FP=GP.在点E运动的过程中,OE的长不变,则FG的长不变,OP、EP的长不变;在点E运动的过程中,点P到AB、CD的距离是变化的.
8. 答案 C 由题意知,OA=OF=OB=OE,
∴∠OAF=∠AFO=∠BOF,∠OBE=∠BEO=∠AOE.
∴∠AGE=∠OAF+∠OBE=(∠BOF+∠AOE)
=(180°-∠EOF)=×(180°-90°)=45°
.故选C.
二、填空题
9.答案 OA、OB、OC;AC、AB、BC;AC;、、、、;、
解析 点O为☉O的圆心,则线段OA、OB、OC是圆O的半径;线段AC、AB、BC是圆O的弦,其中最长的弦是AC;、、、、是劣弧;、是半圆.
10.答案 20°
解析 ∵CB=CD,∴∠B=∠CDB.
∵∠B+∠CDB+∠BCD=180°,∠BCD=40°,
∴∠B=×(180°-∠BCD)=×(180°-40°)=70°.
∵∠ACB=90°,
∴∠A=90°-∠B=20°.
11. 答案 60°
解析 如图,连接OB,
∵∠BDO=15°,OB=OD,
∴∠OBD=∠BDO=15°,
∴∠BOD=150°.
∵OD⊥AC,
∴∠DOC=90°,
∴∠BOC=150°-90°=60°,
又OB=OC,
∴△BOC是等边三角形,∴∠ACB=60°.
12. 答案 22.5
解析 ∵AB是☉O的直径,
∴AB=2DO,
∵AB=2DE,∴DO=DE,
∴∠DOE=∠E.
∵△COD为直角三角形,OC=OD,
∴△COD为等腰直角三角形,
∴∠CDO=45°,
∵∠CDO=∠DOE+∠E,
∴∠E=∠CDO=22.5°.
三、解答题
13.解析 直径:AB.
半径:OA、OB、OC.
弦:CD、AB.
14.解析 如图,连接AC,BD相交于点O,连接OE,OF,OG,OH,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC,AC⊥BD,
∵点E是AB的中点,∴OE=AB.
同理:OF=BC,OG=CD,OH=AD,
∴OE=OF=OG=OH,
∴E、F、G、H四点在以AC,BD的交点O为圆心的同一个圆上.
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.1 圆
一、选择题
1. 小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定错误的是( )
A.4 B.5 C.10 D.11
2. 下列说法中,正确的是( )
A.两个半圆是等弧 B.同圆中优弧与半圆的差必是劣弧
C.长度相等的弧是等弧 D.同圆中优弧与劣弧的差必是优弧
3.如图所示,点M是☉O上的任意一点,下列结论:
①以M为端点的弦只有一条;②以M为端点的半径只有一条;③以M为端点的直径只有一条;④以M为端点的弧只有一条.
其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,OA是☉O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交☉O于点C.以OB、BC为边作矩形OBCD,连接BD.若CD=6,BC=8,则AB的长为( )
A.6 B.5 C.4 D.2
5.如图,BC是☉O的直径,AB是☉O的弦,若∠AOC=60°,则∠OAB的度数是( )
A.20° B.25°
C.30° D.35°
6.下列说法:①直径是最长的弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半径相等的两个圆是等圆,其中说法正确的有( )
A.1个 B.2个
C.3个 D.4个
7.如图,AB,CD是☉O的两条相互垂直的直径,点E是☉O上的动点,过点E作EF⊥AB于F,EG⊥CD于G,连接FG,FG的中点为P.若点E在圆周上运动一周,下列结论错误的是( )
A.FG的长不变
B.点P到点O的距离不变
C.点P到点E的距离不变
D.点P到AB、CD的距离不变
8.如图,AB是☉O的直径,将一直角三角尺的直角顶点放在点O处,两直角边分别与☉O交于E,F两点,连接AF,BE交于点G,则∠AGE的度数为( )
A.30° B.40°
C.45° D.60°
二、填空题
9.如图,若点O为☉O的圆心,则线段 是☉O的半径;线段 是☉O的弦,其中最长的弦是 ; 是劣弧; 是半圆.
10.如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,连接CD,∠BCD=40°,则∠A= .
11.如图,AC为☉O的直径,点B在圆上,OD⊥AC交☉O于点D,连接BD,∠BDO=15°,则∠ACB= .
12.如图,AB是☉O的直径,CD是☉O的弦,AB、CD的延长线交于点E,已知AB=2DE,若△COD为直角三角形,则∠E的度数为 °.
三、解答题
13.如图,线段AB过圆心O,点A,B,C,D均在☉O上,请指出哪些是直径、半径、弦,并把它们表示出来.
14.已知四边形ABCD为菱形,点E、F、G、H分别为各边的中点,判断E、F、G、H四点是否在同一个圆上,如果在同一个圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
答案全解全析
一、选择题
1.答案 D ∵半径为5的圆的直径为10,∴在半径为5的圆中测量弦AB的长度,AB的取值范围是0
3.答案 B 以M为端点的弦有无数条,所以①中结论错误;②正确;③正确;以M为端点的弧有无数条,所以④中结论错误.故选B.
4.答案 C 如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,OB=CD=6,BC=8,
∴OA=OC==10,∴AB=OA-OB=4.故选C.
5. 答案 C ∵∠AOC=60°,∴∠BOA=180°-60°=120°,
∵OA=OB,
∴∠OAB=∠B==30°.
6. 答案 C ①直径是最长的弦,正确;②过圆心的弦才是直径,故原说法错误;③半径相等的两个半圆是等弧,正确;④长度相等的两条弧不一定是等弧,故原说法错误;⑤半径相等的两个圆是等圆,正确.
7. 答案 D 由题意知,四边形OFEG是矩形,连接OE,则OE=FG,点P为OE与FG的交点,OP=EP=FP=GP.在点E运动的过程中,OE的长不变,则FG的长不变,OP、EP的长不变;在点E运动的过程中,点P到AB、CD的距离是变化的.
8. 答案 C 由题意知,OA=OF=OB=OE,
∴∠OAF=∠AFO=∠BOF,∠OBE=∠BEO=∠AOE.
∴∠AGE=∠OAF+∠OBE=(∠BOF+∠AOE)
=(180°-∠EOF)=×(180°-90°)=45°
.故选C.
二、填空题
9.答案 OA、OB、OC;AC、AB、BC;AC;、、、、;、
解析 点O为☉O的圆心,则线段OA、OB、OC是圆O的半径;线段AC、AB、BC是圆O的弦,其中最长的弦是AC;、、、、是劣弧;、是半圆.
10.答案 20°
解析 ∵CB=CD,∴∠B=∠CDB.
∵∠B+∠CDB+∠BCD=180°,∠BCD=40°,
∴∠B=×(180°-∠BCD)=×(180°-40°)=70°.
∵∠ACB=90°,
∴∠A=90°-∠B=20°.
11. 答案 60°
解析 如图,连接OB,
∵∠BDO=15°,OB=OD,
∴∠OBD=∠BDO=15°,
∴∠BOD=150°.
∵OD⊥AC,
∴∠DOC=90°,
∴∠BOC=150°-90°=60°,
又OB=OC,
∴△BOC是等边三角形,∴∠ACB=60°.
12. 答案 22.5
解析 ∵AB是☉O的直径,
∴AB=2DO,
∵AB=2DE,∴DO=DE,
∴∠DOE=∠E.
∵△COD为直角三角形,OC=OD,
∴△COD为等腰直角三角形,
∴∠CDO=45°,
∵∠CDO=∠DOE+∠E,
∴∠E=∠CDO=22.5°.
三、解答题
13.解析 直径:AB.
半径:OA、OB、OC.
弦:CD、AB.
14.解析 如图,连接AC,BD相交于点O,连接OE,OF,OG,OH,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC,AC⊥BD,
∵点E是AB的中点,∴OE=AB.
同理:OF=BC,OG=CD,OH=AD,
∴OE=OF=OG=OH,
∴E、F、G、H四点在以AC,BD的交点O为圆心的同一个圆上.
同课章节目录
