2022-2023学年 人教版九年级数学上册24.1.3 弧、弦、圆心角 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年 人教版九年级数学上册24.1.3 弧、弦、圆心角 章节培优训练试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 371.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 00:00:00 | ||
图片预览


文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
一、选择题
1. 下列图形中,∠AOB为圆心角的是( )
A B C D
2. 下列三个命题:
①同圆或等圆中,相等的弦所对的弧相等;
②同圆或等圆中,相等的弧所对的弦相等;
③同圆或等圆中,相等的弧所对的圆心角相等.
其中真命题有( )
A.0个 B.1个 C.2个 D.3个
3. 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC所在直线折叠,恰好经过点O,则与的关系是( )
A.= B.= C.= D.不能确定
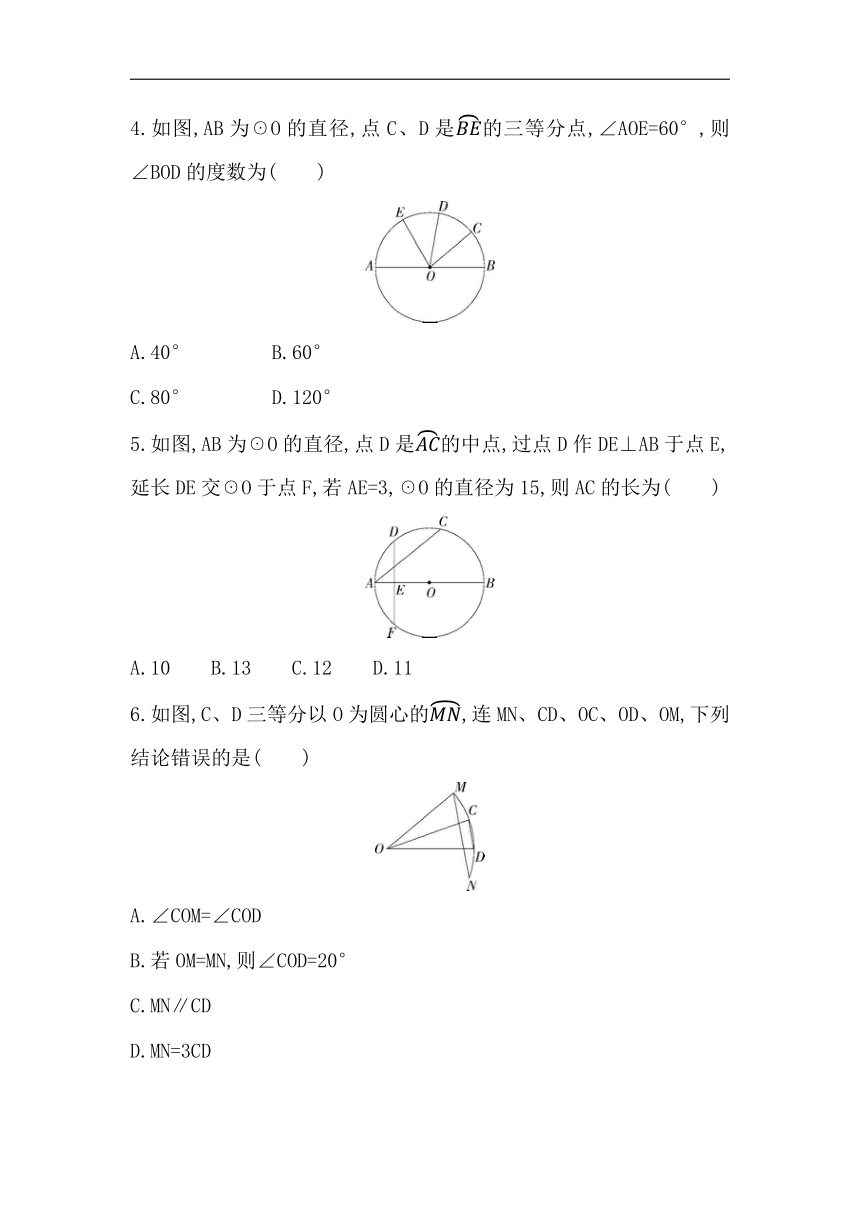
4.如图,AB为☉O的直径,点C、D是的三等分点,∠AOE=60°,则∠BOD的度数为( )
A.40° B.60°
C.80° D.120°
5.如图,AB为☉O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交☉O于点F,若AE=3,☉O的直径为15,则AC的长为( )
A.10 B.13 C.12 D.11
6.如图,C、D三等分以O为圆心的,连MN、CD、OC、OD、OM,下列结论错误的是( )
A.∠COM=∠COD
B.若OM=MN,则∠COD=20°
C.MN∥CD
D.MN=3CD
二、填空题
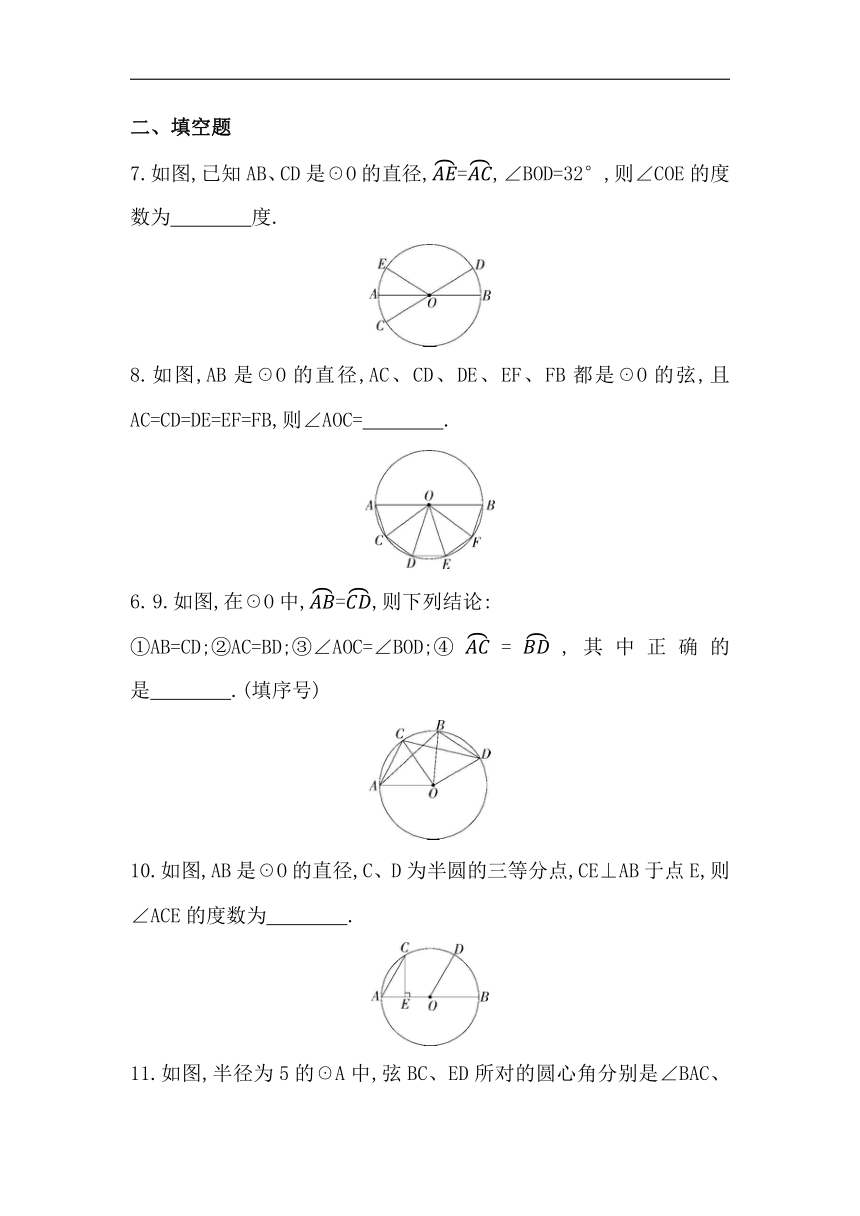
7.如图,已知AB、CD是☉O的直径,=,∠BOD=32°,则∠COE的度数为 度.
8.如图,AB是☉O的直径,AC、CD、DE、EF、FB都是☉O的弦,且AC=CD=DE=EF=FB,则∠AOC= .
9.如图,在☉O中,=,则下列结论:
①AB=CD;②AC=BD;③∠AOC=∠BOD;④=,其中正确的是 .(填序号)
10.如图,AB是☉O的直径,C、D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为 .
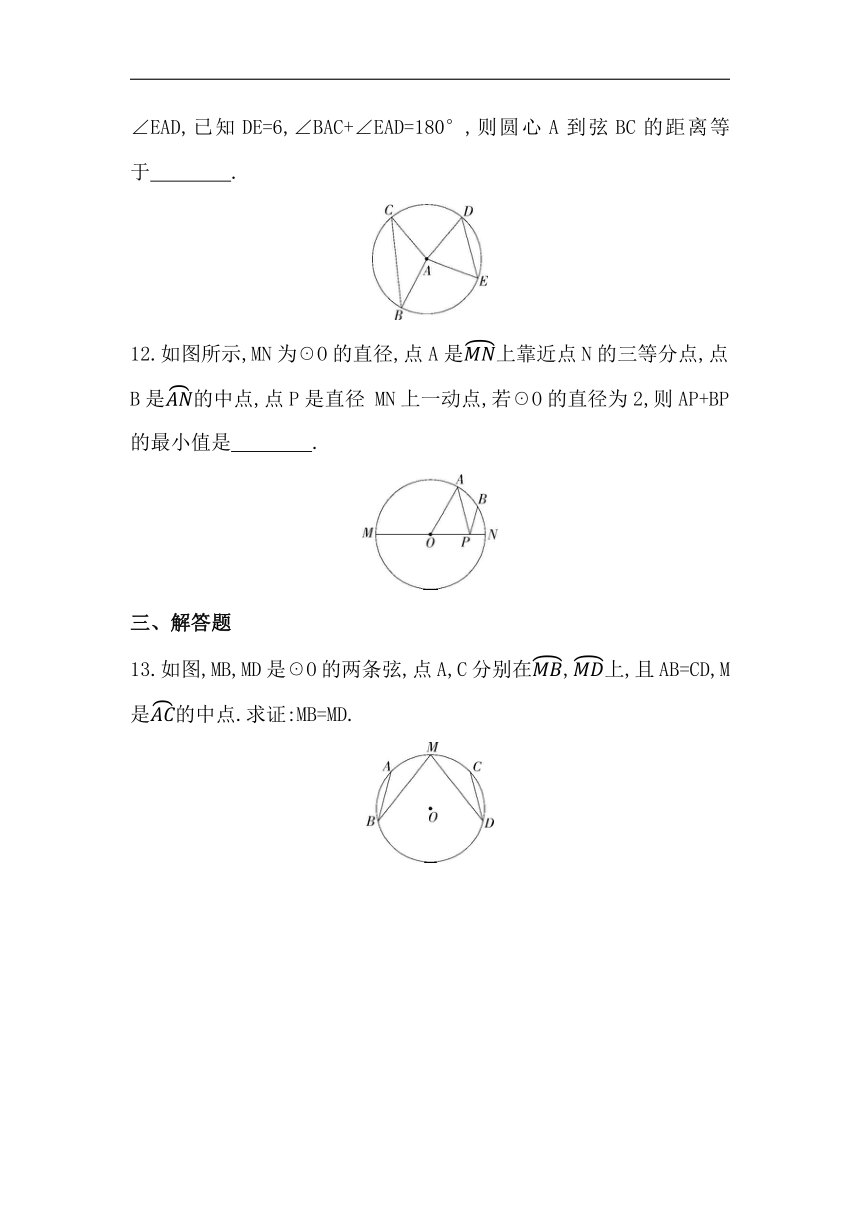
11.如图,半径为5的☉A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于 .
12.如图所示,MN为☉O的直径,点A是上靠近点N的三等分点,点B是的中点,点P是直径 MN上一动点,若☉O的直径为2,则AP+BP的最小值是 .
三、解答题
13.如图,MB,MD是☉O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.求证:MB=MD.
14.如图,AB为☉O的弦,半径OC,OD分别交AB于点E,F,且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
15.如图,AB、CD是☉O的两条弦,=,OE⊥AB,OF⊥CD,垂足分别为E、F.求证:OE=OF.
答案全解全析
一、选择题
1.答案 C 选项A,顶点不是圆心,故选项A不符合题意;选项B,顶点在圆上,∠AOB不是圆心角,故选项B不符合题意;选项C,∠AOB的顶点是圆心,两边与圆相交,故选项C符合题意;选项D,顶点在圆上,∠AOB不是圆心角,故选项D不符合题意.故选C.
2.答案 C 同圆或等圆中,相等的弦所对的优弧、劣弧分别相等,故①是假命题;②是真命题;③是真命题.真命题有2个.故选C.
3.答案 A 如图,作OD⊥AC交半圆O于D,连接AD,OC,则D是的中点,∴∠AOD=∠COD.又由折叠知AD=OA,
∴AD=OA=OD,∴△OAD是等边三角形,
∴∠AOD=60°,
∴∠COD=60°,
∴∠BOC=60°,
∴∠AOD=∠COD=∠BOC=60°,
∴=.故选A.
4. 答案 C ∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,
∵点C、D是的三等分点,
∴∠BOD=×120°=80°.
5. 答案 C 如图,连接OF,∵DE⊥AB,AB为☉O的直径,
∴DE=EF,=,
∵D为的中点,
∴=,
∴=,
∴AC=DF.
∵☉O的直径为15,
∴OF=OA=.
∵AE=3,
∴OE=OA-AE=,
在Rt△OEF中,由勾股定理得EF===6,
∴DE=EF=6,∴AC=DF=DE+EF=6+6=12.
6. 答案 D 如图,连接ON、MC、DN,过点O作OE⊥CD交于点E,
∵=,∴∠COM=∠COD,故A正确;当OM=MN时,
∵OM=ON,∴OM=ON=MN,
∴△OMN为等边三角形,
∴∠MON=60°,
∵==,
∴∠COM=∠COD=∠DON,
∴∠COD=20°,故B正确;
∵OE⊥CD,
∴=,∴=,
∴OE⊥MN,∴MN∥CD,故C正确;
∵==,
∴MC=CD=DN,
∵MC+CD+DN>MN,∴MN<3CD,故D错误.
二、填空题
7.答案 64
解析 ∵∠BOD=32°,
∴∠AOC=∠BOD=32°,
∵=,
∴∠AOE=∠AOC=32°,
∴∠COE=∠AOC+∠AOE=32°+32°=64°.
8.答案 36°
解析 ∵AC=CD=DE=EF=FB,∴∠AOC=∠COD=∠DOE=∠EOF=∠BOF,
∵∠AOB=180°,∴∠AOC=∠AOB=36°.
9.答案 ①②③④
解析 在☉O中,=,∴AB=CD,=,∴AC=BD,∠AOC=∠BOD,故①②③④均正确.
10. 答案 30°
解析 如图,连接OC.∵AB是直径,==,
∴∠AOC=∠COD=∠DOB=60°.
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°,
∵CE⊥OA,∴∠AEC=90°,
∴∠ACE=90°-60°=30°.
11. 答案 3
解析 如图,作AH⊥BC于H,作直径CF,连接BF.
∵∠BAC+∠EAD=180°,∠BAC+∠BAF=180°,
∴∠BAF=∠DAE,∴=,
∴BF=DE=6.
∵AH⊥BC,∴CH=BH,
∵CA=AF,∴AH为△CBF的中位线,
∴AH=BF=3.∴点A到弦BC的距离为3.
12.答案
解析 如图,作点B关于直线MN的对称点B',连接AB'交MN于点P',连接BP',OB',OB.∵点B和点B'关于直线MN对称,
∴P'B=P'B',=,AP'+BP'=AP'+B'P'=AB',
易知点P位于点P'处时,AP+BP的值最小.
∵点A是上靠近点N的三等分点,点B是的中点,=,
∴∠AON=180°÷3=60°,∠B'ON=∠BON=∠AON=30°,∴∠AOB'=∠AON+∠B'ON=90°.∵OA=OB'=1,∴AB'=,故AP+BP的最小值为.
三、解答题
13.证明 ∵M是的中点,∴=,
∵AB=CD,∴=,
∴+=+,即=,
∴MB=MD.
14.解析 (1)证明:如图1,连接OA、OB,
∵OA=OB,∴∠A=∠B.
∵=,∴∠AOE=∠BOF.
在△AOE和△BOF中,
∴△AOE≌△BOF(ASA),∴AE=BF.
图1 图2
(2)如图2,连接OA,∵OM⊥AB,∴AM=AB=6,设OM=x,则OA=ON=x+3,
在Rt△AOM中,由勾股定理得62+x2=(x+3)2,
解得x=4.5,∴OM=4.5.
15.证明 如图,连接OA、OC,
∵=,∴AB=CD.
∵OE⊥AB,OF⊥CD,
∴AE=AB,CF=CD,∠AEO=∠CFO=90°,
∴AE=CF,
又∵OA=OC,
∴Rt△OAE≌Rt△OCF(HL),
∴OE=OF.
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
一、选择题
1. 下列图形中,∠AOB为圆心角的是( )
A B C D
2. 下列三个命题:
①同圆或等圆中,相等的弦所对的弧相等;
②同圆或等圆中,相等的弧所对的弦相等;
③同圆或等圆中,相等的弧所对的圆心角相等.
其中真命题有( )
A.0个 B.1个 C.2个 D.3个
3. 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC所在直线折叠,恰好经过点O,则与的关系是( )
A.= B.= C.= D.不能确定
4.如图,AB为☉O的直径,点C、D是的三等分点,∠AOE=60°,则∠BOD的度数为( )
A.40° B.60°
C.80° D.120°
5.如图,AB为☉O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交☉O于点F,若AE=3,☉O的直径为15,则AC的长为( )
A.10 B.13 C.12 D.11
6.如图,C、D三等分以O为圆心的,连MN、CD、OC、OD、OM,下列结论错误的是( )
A.∠COM=∠COD
B.若OM=MN,则∠COD=20°
C.MN∥CD
D.MN=3CD
二、填空题
7.如图,已知AB、CD是☉O的直径,=,∠BOD=32°,则∠COE的度数为 度.
8.如图,AB是☉O的直径,AC、CD、DE、EF、FB都是☉O的弦,且AC=CD=DE=EF=FB,则∠AOC= .
9.如图,在☉O中,=,则下列结论:
①AB=CD;②AC=BD;③∠AOC=∠BOD;④=,其中正确的是 .(填序号)
10.如图,AB是☉O的直径,C、D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为 .
11.如图,半径为5的☉A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于 .
12.如图所示,MN为☉O的直径,点A是上靠近点N的三等分点,点B是的中点,点P是直径 MN上一动点,若☉O的直径为2,则AP+BP的最小值是 .
三、解答题
13.如图,MB,MD是☉O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.求证:MB=MD.
14.如图,AB为☉O的弦,半径OC,OD分别交AB于点E,F,且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
15.如图,AB、CD是☉O的两条弦,=,OE⊥AB,OF⊥CD,垂足分别为E、F.求证:OE=OF.
答案全解全析
一、选择题
1.答案 C 选项A,顶点不是圆心,故选项A不符合题意;选项B,顶点在圆上,∠AOB不是圆心角,故选项B不符合题意;选项C,∠AOB的顶点是圆心,两边与圆相交,故选项C符合题意;选项D,顶点在圆上,∠AOB不是圆心角,故选项D不符合题意.故选C.
2.答案 C 同圆或等圆中,相等的弦所对的优弧、劣弧分别相等,故①是假命题;②是真命题;③是真命题.真命题有2个.故选C.
3.答案 A 如图,作OD⊥AC交半圆O于D,连接AD,OC,则D是的中点,∴∠AOD=∠COD.又由折叠知AD=OA,
∴AD=OA=OD,∴△OAD是等边三角形,
∴∠AOD=60°,
∴∠COD=60°,
∴∠BOC=60°,
∴∠AOD=∠COD=∠BOC=60°,
∴=.故选A.
4. 答案 C ∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,
∵点C、D是的三等分点,
∴∠BOD=×120°=80°.
5. 答案 C 如图,连接OF,∵DE⊥AB,AB为☉O的直径,
∴DE=EF,=,
∵D为的中点,
∴=,
∴=,
∴AC=DF.
∵☉O的直径为15,
∴OF=OA=.
∵AE=3,
∴OE=OA-AE=,
在Rt△OEF中,由勾股定理得EF===6,
∴DE=EF=6,∴AC=DF=DE+EF=6+6=12.
6. 答案 D 如图,连接ON、MC、DN,过点O作OE⊥CD交于点E,
∵=,∴∠COM=∠COD,故A正确;当OM=MN时,
∵OM=ON,∴OM=ON=MN,
∴△OMN为等边三角形,
∴∠MON=60°,
∵==,
∴∠COM=∠COD=∠DON,
∴∠COD=20°,故B正确;
∵OE⊥CD,
∴=,∴=,
∴OE⊥MN,∴MN∥CD,故C正确;
∵==,
∴MC=CD=DN,
∵MC+CD+DN>MN,∴MN<3CD,故D错误.
二、填空题
7.答案 64
解析 ∵∠BOD=32°,
∴∠AOC=∠BOD=32°,
∵=,
∴∠AOE=∠AOC=32°,
∴∠COE=∠AOC+∠AOE=32°+32°=64°.
8.答案 36°
解析 ∵AC=CD=DE=EF=FB,∴∠AOC=∠COD=∠DOE=∠EOF=∠BOF,
∵∠AOB=180°,∴∠AOC=∠AOB=36°.
9.答案 ①②③④
解析 在☉O中,=,∴AB=CD,=,∴AC=BD,∠AOC=∠BOD,故①②③④均正确.
10. 答案 30°
解析 如图,连接OC.∵AB是直径,==,
∴∠AOC=∠COD=∠DOB=60°.
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°,
∵CE⊥OA,∴∠AEC=90°,
∴∠ACE=90°-60°=30°.
11. 答案 3
解析 如图,作AH⊥BC于H,作直径CF,连接BF.
∵∠BAC+∠EAD=180°,∠BAC+∠BAF=180°,
∴∠BAF=∠DAE,∴=,
∴BF=DE=6.
∵AH⊥BC,∴CH=BH,
∵CA=AF,∴AH为△CBF的中位线,
∴AH=BF=3.∴点A到弦BC的距离为3.
12.答案
解析 如图,作点B关于直线MN的对称点B',连接AB'交MN于点P',连接BP',OB',OB.∵点B和点B'关于直线MN对称,
∴P'B=P'B',=,AP'+BP'=AP'+B'P'=AB',
易知点P位于点P'处时,AP+BP的值最小.
∵点A是上靠近点N的三等分点,点B是的中点,=,
∴∠AON=180°÷3=60°,∠B'ON=∠BON=∠AON=30°,∴∠AOB'=∠AON+∠B'ON=90°.∵OA=OB'=1,∴AB'=,故AP+BP的最小值为.
三、解答题
13.证明 ∵M是的中点,∴=,
∵AB=CD,∴=,
∴+=+,即=,
∴MB=MD.
14.解析 (1)证明:如图1,连接OA、OB,
∵OA=OB,∴∠A=∠B.
∵=,∴∠AOE=∠BOF.
在△AOE和△BOF中,
∴△AOE≌△BOF(ASA),∴AE=BF.
图1 图2
(2)如图2,连接OA,∵OM⊥AB,∴AM=AB=6,设OM=x,则OA=ON=x+3,
在Rt△AOM中,由勾股定理得62+x2=(x+3)2,
解得x=4.5,∴OM=4.5.
15.证明 如图,连接OA、OC,
∵=,∴AB=CD.
∵OE⊥AB,OF⊥CD,
∴AE=AB,CF=CD,∠AEO=∠CFO=90°,
∴AE=CF,
又∵OA=OC,
∴Rt△OAE≌Rt△OCF(HL),
∴OE=OF.
同课章节目录
