2022-2023学年人教版九年级数学上册24.1.4.1圆周角定理及其推论 章节培优训练试卷(word版含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册24.1.4.1圆周角定理及其推论 章节培优训练试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 328.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 09:03:09 | ||
图片预览


文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
第1课时 圆周角定理及其推论
一、选择题
1. 能说明圆上一条弧所对的圆周角等于它所对圆心角的一半的图形是( )
A B C D
2. 如图,点A,B,C在☉O上,∠BAC=54°,则∠BOC的度数为( )
A.27° B.108° C.116° D.128°
3. 如图,AB是☉O的直径,AC,BC是☉O的弦,若∠A=20°,则∠B的度数为( )
A.70° B.90° C.40° D.60°
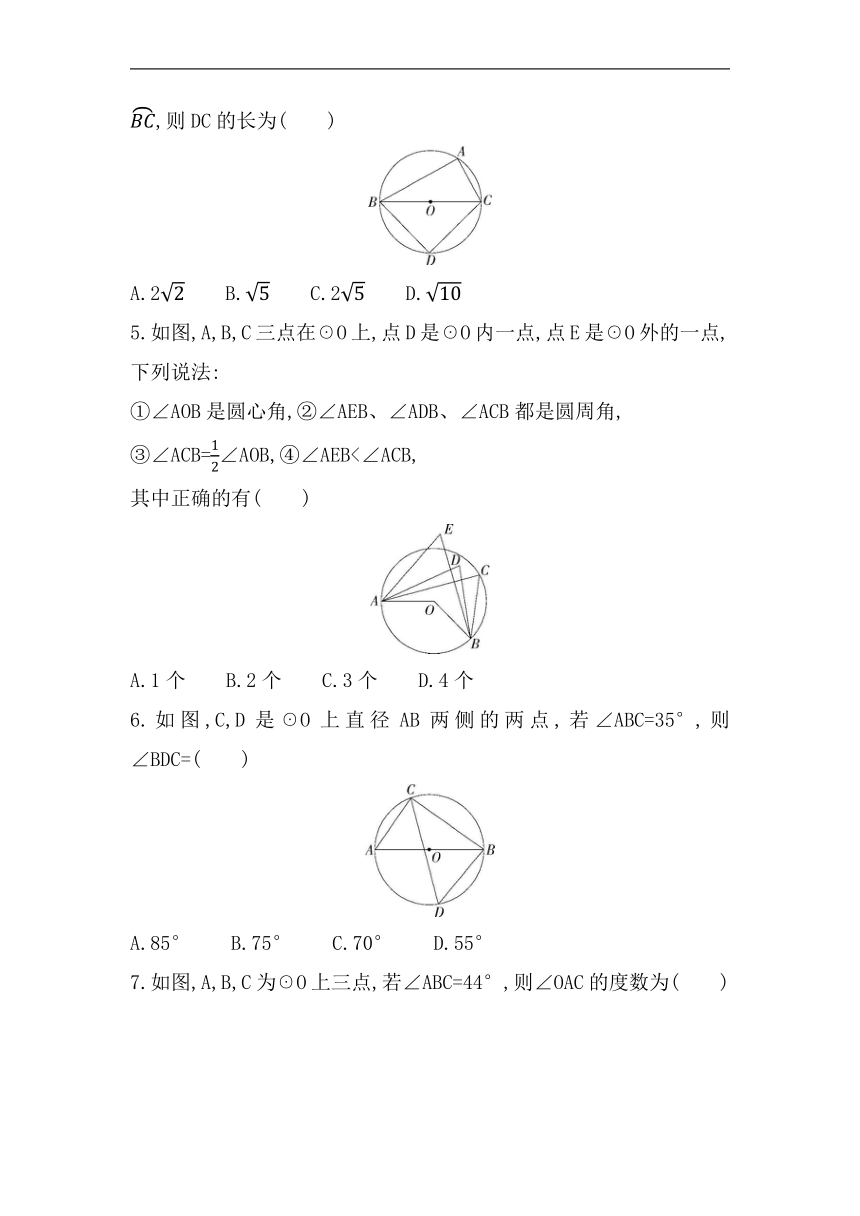
4. 如图,A是☉O上一点,BC是直径,AC=2,AB=4,点D在☉O上,且平分,则DC的长为( )
A.2 B. C.2 D.
5.如图,A,B,C三点在☉O上,点D是☉O内一点,点E是☉O外的一点,下列说法:
①∠AOB是圆心角,②∠AEB、∠ADB、∠ACB都是圆周角,
③∠ACB=∠AOB,④∠AEB<∠ACB,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,C,D是☉O上直径AB两侧的两点,若∠ABC=35°,则∠BDC=( )
A.85° B.75° C.70° D.55°
7.如图,A,B,C为☉O上三点,若∠ABC=44°,则∠OAC的度数为( )
A.46° B.44°
C.40° D.50°
8.如图,点A,B,C,D,E在☉O上,AB=CD,∠AOB=42°,则∠CED=( )
A.48° B.24° C.22° D.21°
二、填空题
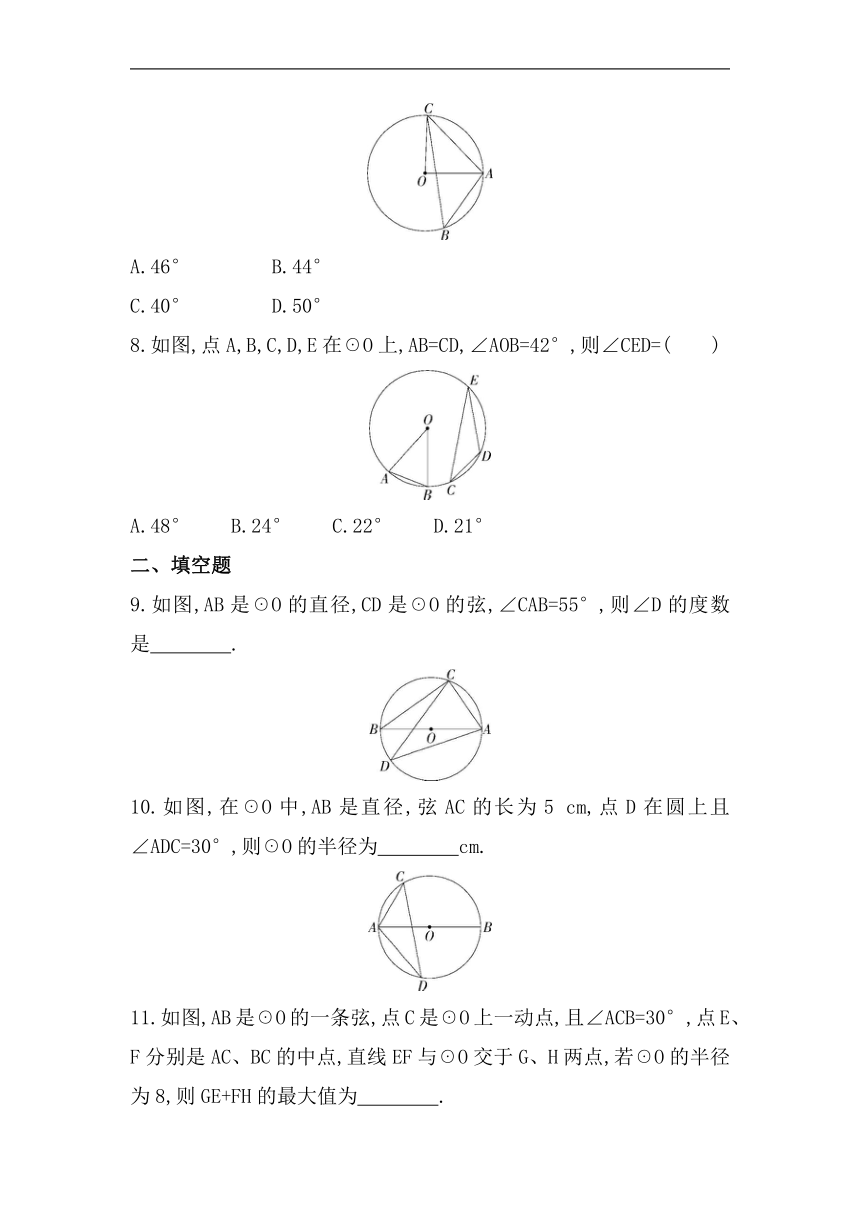
9.如图,AB是☉O的直径,CD是☉O的弦,∠CAB=55°,则∠D的度数是 .
10.如图,在☉O中,AB是直径,弦AC的长为5 cm,点D在圆上且∠ADC=30°,则☉O的半径为 cm.
11.如图,AB是☉O的一条弦,点C是☉O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与☉O交于G、H两点,若☉O的半径为8,则GE+FH的最大值为 .
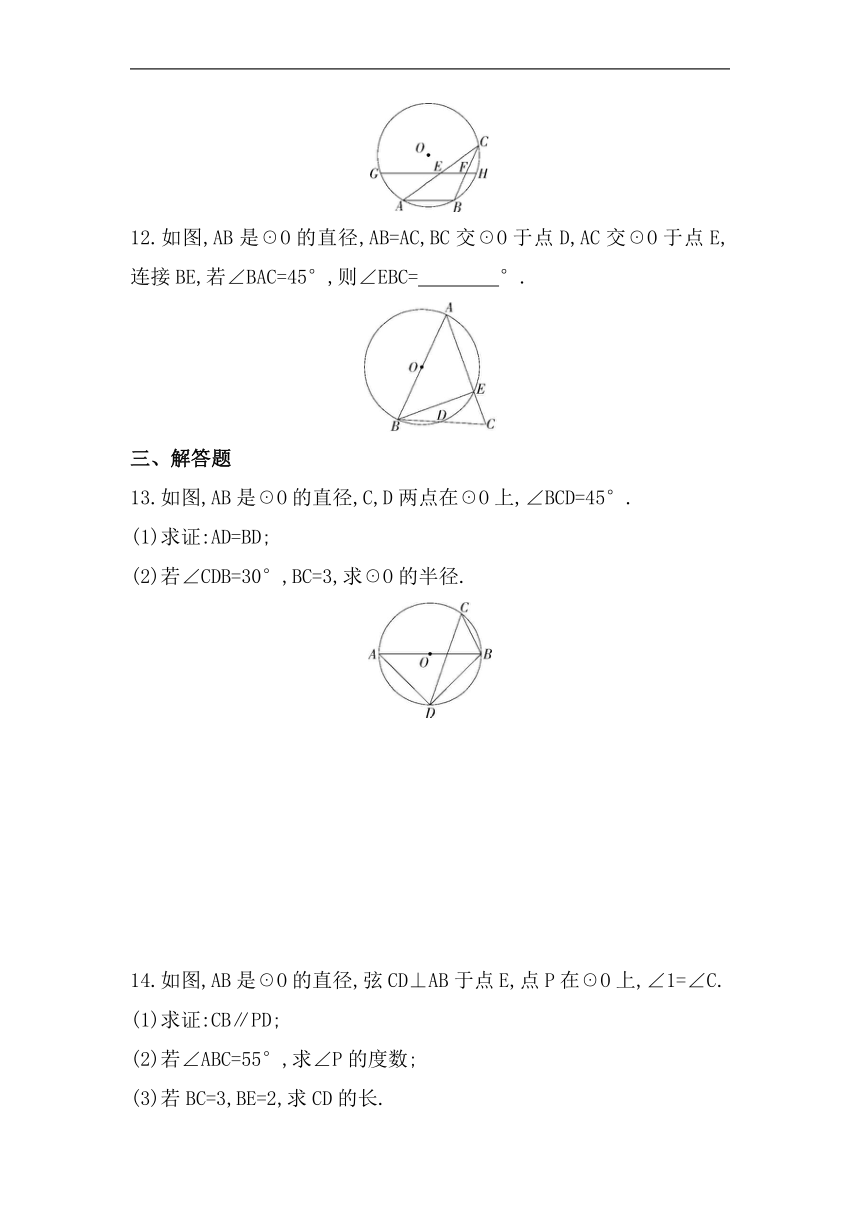
12.如图,AB是☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E,连接BE,若∠BAC=45°,则∠EBC= °.
三、解答题
13.如图,AB是☉O的直径,C,D两点在☉O上,∠BCD=45°.
(1)求证:AD=BD;
(2)若∠CDB=30°,BC=3,求☉O的半径.
14.如图,AB是☉O的直径,弦CD⊥AB于点E,点P在☉O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若∠ABC=55°,求∠P的度数;
(3)若BC=3,BE=2,求CD的长.
答案全解全析
一、选择题
1.答案 A 根据三角形外角的性质由A选项的图形可得∠BAC=∠BOC.故选A.
2.答案 B ∵∠A=54°,∴∠BOC=2∠A=108°.故选B.
3.答案 A ∵AB是☉O的直径,∴∠C=90°,
∵∠A=20°,∴∠B=90°-∠A=70°.故选A.
4.答案 D
∵BC是☉O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴BC2=AB2+AC2=22+42=20,
∵点D在☉O上,且平分,
∴=,∴CD=BD.Rt△BDC中,DC2+BD2=BC2,∴2DC2=20,∴DC=.故选D.
5. 答案 C 由题意知,∠AOB是圆心角,∠ACB是圆周角,∠AEB和∠ADB不是圆周角,故①正确,②不正确;如图,设AE与☉O相交于F,连接BF,则∠AFB和∠ACB都是所对的圆周角,
∴∠AFB=∠ACB=∠AOB,故③正确;
∵∠AFB>∠AEB,∴∠AEB<∠ACB,故④正确.故选C.
6. 答案 D ∵AB是☉O的直径,
∴∠ACB=90°.
∵∠ABC=35°,
∴∠CAB=55°,
∴∠BDC=∠CAB=55°.
7. 答案 A ∵∠ABC和∠AOC分别是所对的圆周角和圆心角,
∴∠AOC=2∠ABC=88°.
∵OA=OC,
∴∠OAC=∠OCA==46°.
8. 答案 D 连接AE,BE,
∵∠AOB=42°,
∴∠AEB=∠AOB=21°,
∵AB=CD,
∴=,
∴∠AEB=∠CED,
∴∠CED=21°.
二、填空题
9.答案 35°
解析 ∵AB是☉O的直径,∴∠ACB=90°,
∵∠CAB=55°,∴∠B=90°-∠CAB=35°,∴∠D=∠B=35°.
10.答案 5
解析 如图,连接OC.∵∠ADC=30°,∴∠AOC=2∠ADC=60°.又∵OA=OC,∴△AOC是等边三角形,∴OA=AC=5 cm,∴☉O的半径为5 cm.
11.答案 12
解析 如图,连接OA、OB,
∵∠ACB=30°,∴∠AOB=2∠ACB=60°.∵OA=OB,∴△AOB为等边三角形.∵☉O的半径为8,∴AB=OA=OB=8,∵点E、F分别是AC、BC的中点,∴EF=AB=4,当GE+FH取最大值时,GE+FH+EF(弦GH)取最大值,∵当弦GH是圆的直径时,GH取得最大值,为8×2=16,∴GE+FH的最大值为16-4=12.
12. 答案 22.5
解析 ∵AB是☉O的直径,
∴∠AEB=90°.
∵∠BAC=45°,
∴∠ABE=45°.
∵AB=AC,
∴∠ABC=∠C=×(180°-45°)=67.5°,
∴∠EBC=∠ABC-∠ABE=67.5°-45°=22.5°.
三、解答题
13.解析 (1)证明:∵∠DCB=45°,
∴∠DAB=∠DCB=45°.
∵AB是☉O的直径,
∴∠ADB=90°,
∴∠ABD=45°.
∴∠DAB=∠ABD=45°,
∴AD=BD.
(2)如图,连接OC.
∵∠CDB=30°,
∴∠BOC=60°,又∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC=3,
即☉O的半径为3.
14.解析 (1)证明:∵=,
∴∠P=∠C,
∵∠1=∠C,
∴∠1=∠P,
∴CB∥PD.
(2)∵CD⊥AB,
∴∠CEB=90°,
∵∠CBE=55°,
∴∠C=90°-55°=35°,
∴∠P=∠C=35°.
(3)∵CE⊥BE,
∴CE2=CB2-BE2,
∵CB=3,BE=2,
∴CE=,
∵AB⊥CD,
∴CD=2CE=2.
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
第1课时 圆周角定理及其推论
一、选择题
1. 能说明圆上一条弧所对的圆周角等于它所对圆心角的一半的图形是( )
A B C D
2. 如图,点A,B,C在☉O上,∠BAC=54°,则∠BOC的度数为( )
A.27° B.108° C.116° D.128°
3. 如图,AB是☉O的直径,AC,BC是☉O的弦,若∠A=20°,则∠B的度数为( )
A.70° B.90° C.40° D.60°
4. 如图,A是☉O上一点,BC是直径,AC=2,AB=4,点D在☉O上,且平分,则DC的长为( )
A.2 B. C.2 D.
5.如图,A,B,C三点在☉O上,点D是☉O内一点,点E是☉O外的一点,下列说法:
①∠AOB是圆心角,②∠AEB、∠ADB、∠ACB都是圆周角,
③∠ACB=∠AOB,④∠AEB<∠ACB,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,C,D是☉O上直径AB两侧的两点,若∠ABC=35°,则∠BDC=( )
A.85° B.75° C.70° D.55°
7.如图,A,B,C为☉O上三点,若∠ABC=44°,则∠OAC的度数为( )
A.46° B.44°
C.40° D.50°
8.如图,点A,B,C,D,E在☉O上,AB=CD,∠AOB=42°,则∠CED=( )
A.48° B.24° C.22° D.21°
二、填空题
9.如图,AB是☉O的直径,CD是☉O的弦,∠CAB=55°,则∠D的度数是 .
10.如图,在☉O中,AB是直径,弦AC的长为5 cm,点D在圆上且∠ADC=30°,则☉O的半径为 cm.
11.如图,AB是☉O的一条弦,点C是☉O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与☉O交于G、H两点,若☉O的半径为8,则GE+FH的最大值为 .
12.如图,AB是☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E,连接BE,若∠BAC=45°,则∠EBC= °.
三、解答题
13.如图,AB是☉O的直径,C,D两点在☉O上,∠BCD=45°.
(1)求证:AD=BD;
(2)若∠CDB=30°,BC=3,求☉O的半径.
14.如图,AB是☉O的直径,弦CD⊥AB于点E,点P在☉O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若∠ABC=55°,求∠P的度数;
(3)若BC=3,BE=2,求CD的长.
答案全解全析
一、选择题
1.答案 A 根据三角形外角的性质由A选项的图形可得∠BAC=∠BOC.故选A.
2.答案 B ∵∠A=54°,∴∠BOC=2∠A=108°.故选B.
3.答案 A ∵AB是☉O的直径,∴∠C=90°,
∵∠A=20°,∴∠B=90°-∠A=70°.故选A.
4.答案 D
∵BC是☉O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴BC2=AB2+AC2=22+42=20,
∵点D在☉O上,且平分,
∴=,∴CD=BD.Rt△BDC中,DC2+BD2=BC2,∴2DC2=20,∴DC=.故选D.
5. 答案 C 由题意知,∠AOB是圆心角,∠ACB是圆周角,∠AEB和∠ADB不是圆周角,故①正确,②不正确;如图,设AE与☉O相交于F,连接BF,则∠AFB和∠ACB都是所对的圆周角,
∴∠AFB=∠ACB=∠AOB,故③正确;
∵∠AFB>∠AEB,∴∠AEB<∠ACB,故④正确.故选C.
6. 答案 D ∵AB是☉O的直径,
∴∠ACB=90°.
∵∠ABC=35°,
∴∠CAB=55°,
∴∠BDC=∠CAB=55°.
7. 答案 A ∵∠ABC和∠AOC分别是所对的圆周角和圆心角,
∴∠AOC=2∠ABC=88°.
∵OA=OC,
∴∠OAC=∠OCA==46°.
8. 答案 D 连接AE,BE,
∵∠AOB=42°,
∴∠AEB=∠AOB=21°,
∵AB=CD,
∴=,
∴∠AEB=∠CED,
∴∠CED=21°.
二、填空题
9.答案 35°
解析 ∵AB是☉O的直径,∴∠ACB=90°,
∵∠CAB=55°,∴∠B=90°-∠CAB=35°,∴∠D=∠B=35°.
10.答案 5
解析 如图,连接OC.∵∠ADC=30°,∴∠AOC=2∠ADC=60°.又∵OA=OC,∴△AOC是等边三角形,∴OA=AC=5 cm,∴☉O的半径为5 cm.
11.答案 12
解析 如图,连接OA、OB,
∵∠ACB=30°,∴∠AOB=2∠ACB=60°.∵OA=OB,∴△AOB为等边三角形.∵☉O的半径为8,∴AB=OA=OB=8,∵点E、F分别是AC、BC的中点,∴EF=AB=4,当GE+FH取最大值时,GE+FH+EF(弦GH)取最大值,∵当弦GH是圆的直径时,GH取得最大值,为8×2=16,∴GE+FH的最大值为16-4=12.
12. 答案 22.5
解析 ∵AB是☉O的直径,
∴∠AEB=90°.
∵∠BAC=45°,
∴∠ABE=45°.
∵AB=AC,
∴∠ABC=∠C=×(180°-45°)=67.5°,
∴∠EBC=∠ABC-∠ABE=67.5°-45°=22.5°.
三、解答题
13.解析 (1)证明:∵∠DCB=45°,
∴∠DAB=∠DCB=45°.
∵AB是☉O的直径,
∴∠ADB=90°,
∴∠ABD=45°.
∴∠DAB=∠ABD=45°,
∴AD=BD.
(2)如图,连接OC.
∵∠CDB=30°,
∴∠BOC=60°,又∵OB=OC,
∴△OBC是等边三角形,
∴OB=BC=3,
即☉O的半径为3.
14.解析 (1)证明:∵=,
∴∠P=∠C,
∵∠1=∠C,
∴∠1=∠P,
∴CB∥PD.
(2)∵CD⊥AB,
∴∠CEB=90°,
∵∠CBE=55°,
∴∠C=90°-55°=35°,
∴∠P=∠C=35°.
(3)∵CE⊥BE,
∴CE2=CB2-BE2,
∵CB=3,BE=2,
∴CE=,
∵AB⊥CD,
∴CD=2CE=2.
同课章节目录
