2022-2023学年人教版九年级数学上册24.1.4.2圆内接四边形 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册24.1.4.2圆内接四边形 章节培优训练试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 374.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 00:00:00 | ||
图片预览


文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
第2课时 圆内接四边形
一、选择题
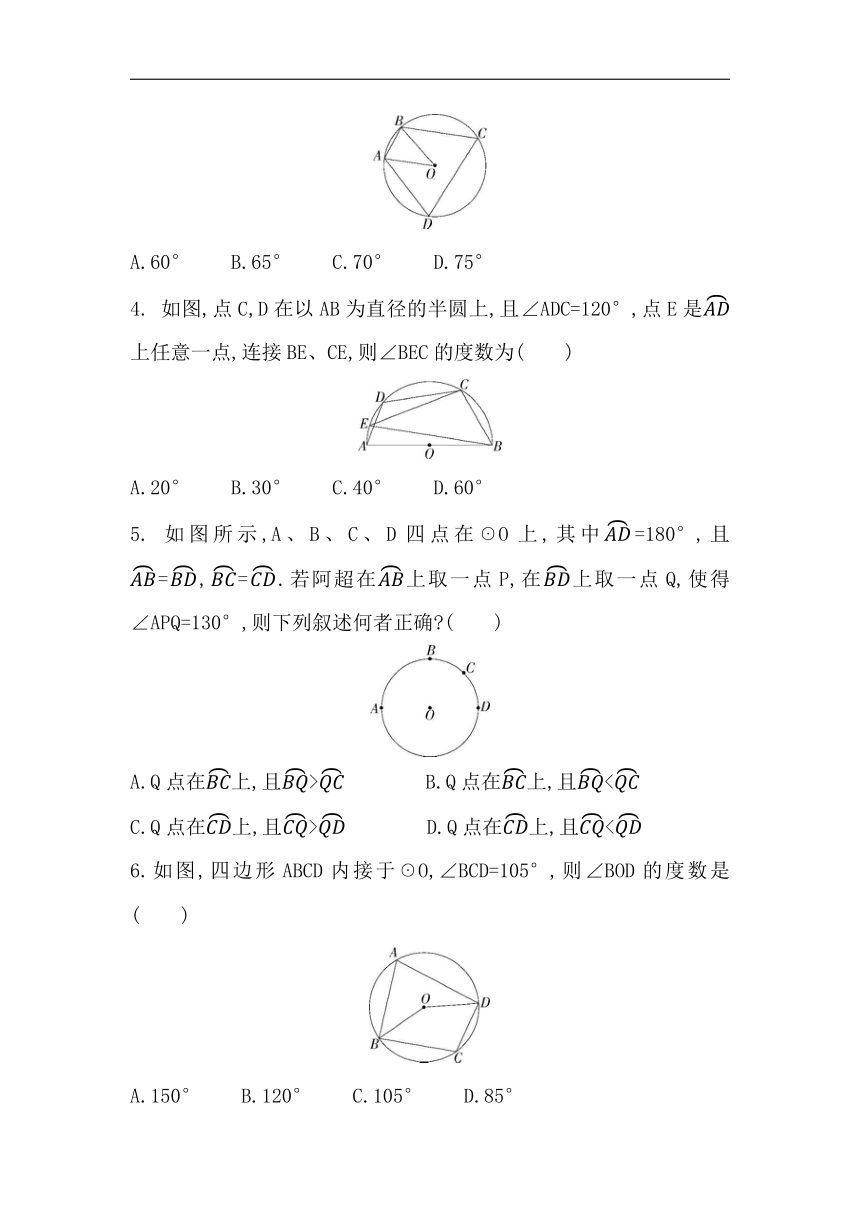
1. 如图,圆内接四边形ABCD的外角∠ABE为80°,则∠ADC的度数为( )
A.80° B.40° C.100° D.160°
2. 如图,四边形ABCD是☉O的内接四边形,BE是☉O的直径,连接AE.若∠BCD=2∠BAD,则∠DAE的度数是( )
A.30° B.35° C.45° D.60°
3. 如图,四边形ABCD内接于☉O,若∠AOB=40°,BC∥OA,则∠ADC的度数为( )
A.60° B.65° C.70° D.75°
4. 如图,点C,D在以AB为直径的半圆上,且∠ADC=120°,点E是上任意一点,连接BE、CE,则∠BEC的度数为( )
A.20° B.30° C.40° D.60°
5. 如图所示,A、B、C、D四点在☉O上,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确 ( )
A.Q点在上,且> B.Q点在上,且<
C.Q点在上,且> D.Q点在上,且<
6.如图,四边形ABCD内接于☉O,∠BCD=105°,则∠BOD的度数是( )
A.150° B.120° C.105° D.85°
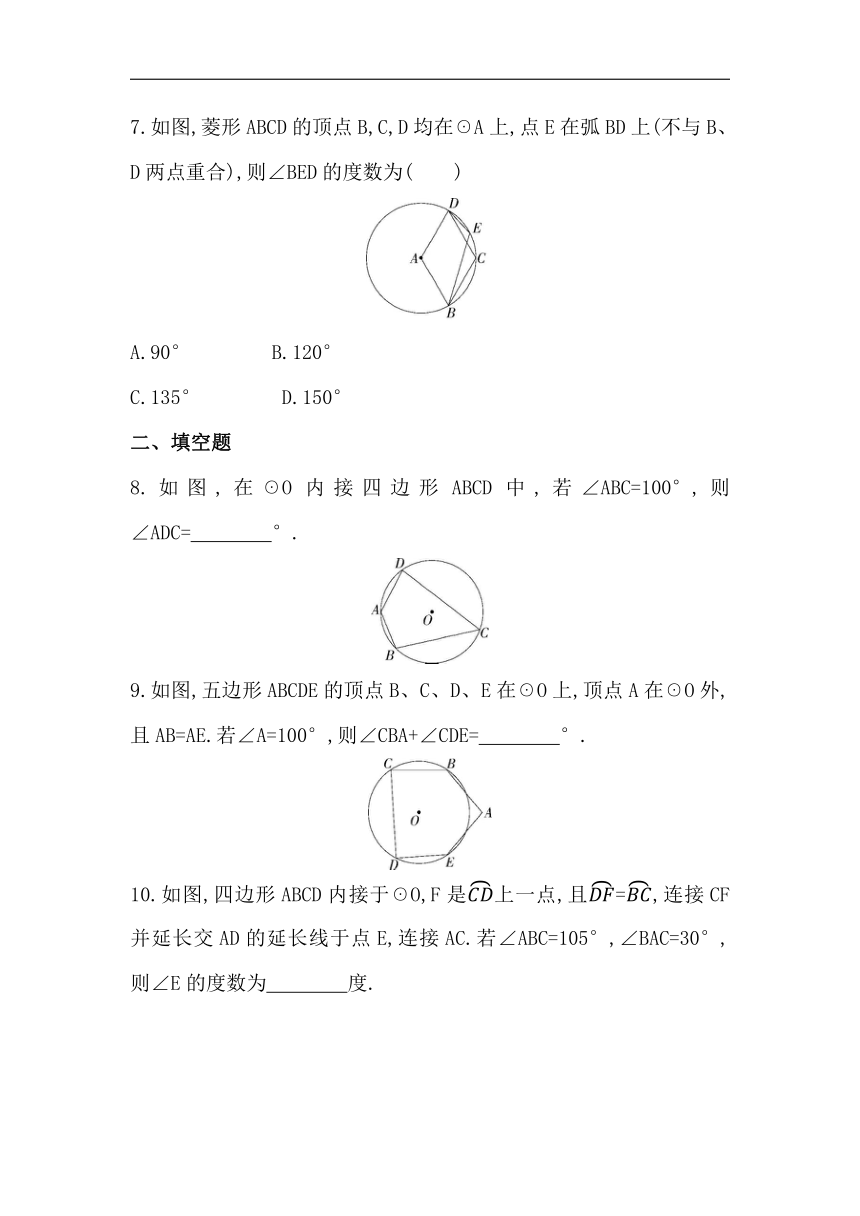
7.如图,菱形ABCD的顶点B,C,D均在☉A上,点E在弧BD上(不与B、D两点重合),则∠BED的度数为( )
A.90° B.120°
C.135° D.150°
二、填空题
8.如图,在☉O内接四边形ABCD中,若∠ABC=100°,则∠ADC= °.
9.如图,五边形ABCDE的顶点B、C、D、E在☉O上,顶点A在☉O外,且AB=AE.若∠A=100°,则∠CBA+∠CDE= °.
10.如图,四边形ABCD内接于☉O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为 度.
11.如图,四边形ABCD是☉O的内接四边形,∠ADC=150°,弦AC=2,则☉O的半径等于 .
12.如图,点A、B、C、D、E在☉O上,所对的圆心角的度数为30°,则∠E+∠C= .
13.如图,☉O上有两个定点A、B,点P是☉O上一动点(不与A、B两点重合),若∠OAB=35°,则∠APB的度数是 .
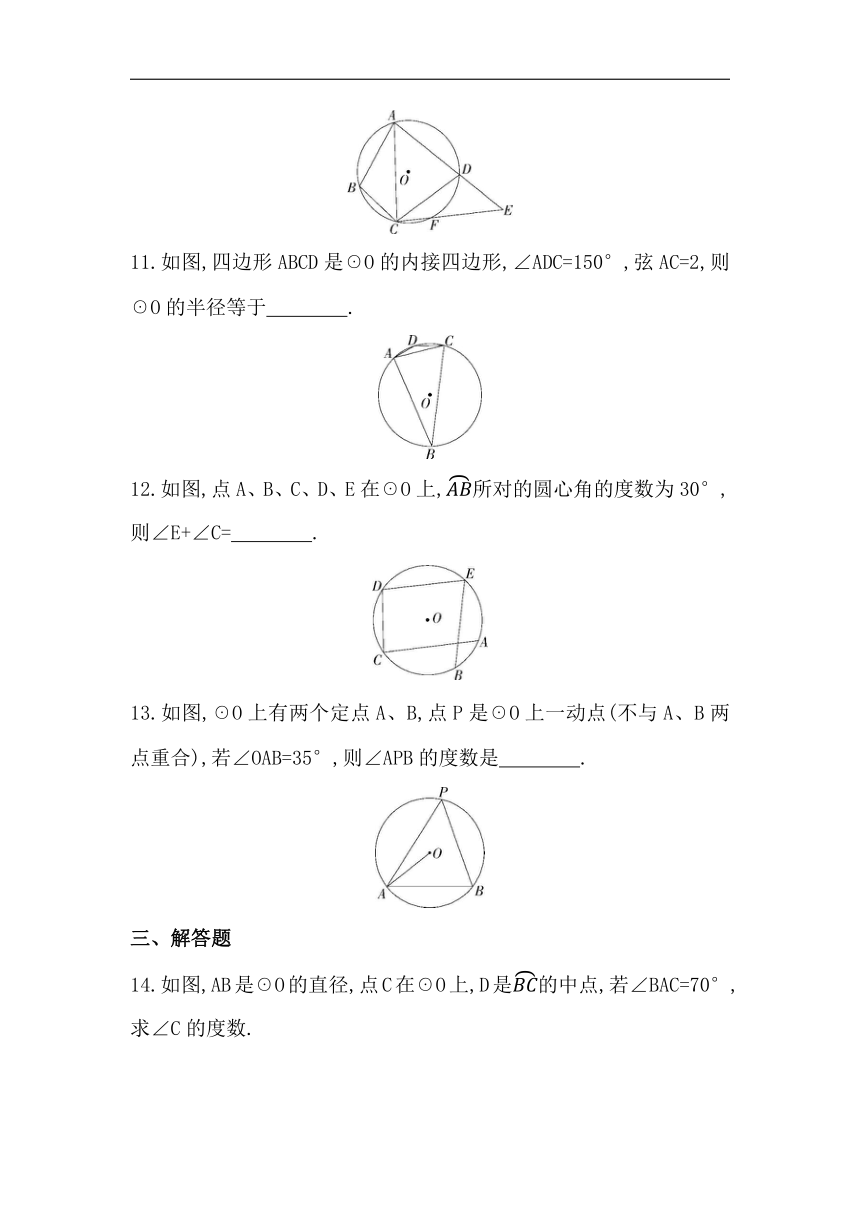
三、解答题
14.如图,AB是☉O的直径,点C在☉O上,D是的中点,若∠BAC=70°,求∠C的度数.
15.如图,四边形ABCD内接于☉O,OC=2,AC=2.
(1)求点O到AC的距离;
(2)求∠ADC的度数.
答案全解全析
一、选择题
1.答案 A ∵四边形ABCD为圆内接四边形,∴∠ADC+∠ABC=180°.
∵∠ABE+∠ABC=180°,∴∠ADC=∠ABE=80°.故选A.
2.答案 A ∵四边形ABCD是☉O的内接四边形,
∴∠BCD+∠BAD=180°,
∵∠BCD=2∠BAD,∴∠BCD=120°,∠BAD=60°,
∵BE是☉O的直径,∴∠BAE=90°,
∴∠DAE=90°-∠BAD=90°-60°=30°,故选A.
3.答案 C
∵BC∥OA,∠AOB=40°,∴∠OBC=∠AOB=40°.
∵OA=OB,∠AOB=40°,
∴∠OBA=×(180°-40°)=70°,
∴∠ABC=∠OBA+∠OBC=70°+40°=110°.
∵四边形ABCD内接于☉O,∴∠ADC=180°-∠ABC=180°-110°=70°.故选C.
4.答案 B 如图,连接AC,
∵四边形ABCD为☉O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ABC=180°-120°=60°.
∵AB为直径,
∴∠ACB=90°,∴∠BAC=90°-60°=30°,
∴∠BEC=∠BAC=30°.故选B.
答案 B 连接AD,OB,OC,∵=180°,且=,=,∴∠AOB=∠BOD=90°,∠BOC=∠DOC=45°,如图,在圆周上取一点E,连接AE,CE,则∠AEC=∠AOC=67.5°,易知当Q位于上时,∠APQ≤180°-67.5°=112.5°,∴Q位于上,取的中点F,连接OF,EF,BE,则∠AOF=∠AOB+∠BOF=90°+22.5°=112.5°,
∴∠AEF=∠AOF=56.25°,又易知∠AEB=∠AOB=45°,∴当Q位于上时,∠APQ≤180°-45°=135°且∠APQ≥180°-56.25°=123.75°,∴Q点在上(不含点B与F),则Q点在上,且<.故选B.
6. 答案 A ∵四边形ABCD内接于☉O,∠BCD=105°,
∴∠A=180°-∠BCD=180°-105°=75°.∴∠BOD=2∠A=2×75°=150°.
7. 答案 B 如图,连接AC.∵四边形ABCD是菱形,AB=AC=AD,
∴AB=BC=CD=AD=AC,∴△ABC,△ACD都是等边三角形,
∴∠ACB=∠ACD=60°,∴∠BCD=120°,
∴∠BED=∠BCD=120°.
二、填空题
8.答案 80
解析 ∵四边形ABCD是☉O的内接四边形,∴∠ABC+∠ADC=180°,∴∠ADC=180°-100°=80°.
9.答案 220
解析 如图,连接BE,∵AB=AE,∠A=100°,
∴∠ABE=∠AEB=(180°-∠A)=40°.
∵点B、C、D、E在☉O上,∴∠CDE+∠CBE=180°,
∴∠CBA+∠CDE=∠CDE+∠CBE+∠ABE=180°+40°=220°.
10.答案 45
解析 ∵=,∠BAC=30°,∴∠DCF=∠BAC=30°.∵四边形ABCD是☉O的内接四边形,
∴∠ADC+∠ABC=180°.
∵∠ABC=105°,∴∠ADC=75°,
∴∠E=∠ADC-∠DCF=75°-30°=45°.
11.答案 2
解析 如图,连接OA,OC,∵四边形ABCD是☉O的内接四边形,
∴∠ADC+∠ABC=180°.∵∠ADC=150°,∴∠ABC=30°,∴∠AOC=2∠ABC=60°.∵OA=OC,∴△OAC为等边三角形,∴OA=AC=2,即☉O的半径为2.
12. 答案 165°
解析 如图,连接EA,
∵所对的圆心角的度数为30°,∴∠AEB=15°.
∵四边形ACDE为☉O的内接四边形,
∴∠C+∠AED=180°,
∴∠C+∠BED=180°-15°=165°.
13. 答案 55°或125°
解析 如图,连接OB.当点P在优弧上时,
∵OA=OB,∴∠OBA=∠OAB=35°,
∴∠AOB=110°,
∴∠P=∠AOB=55°;当点P在劣弧上时,如图中点P'所示,∠AP'B=180°-∠APB=125°.
综上,∠APB=55°或125°.
三、解答题
14.解析 如图,连接AD,
在☉O中,∵D是的中点,
∴=,∴∠1=∠2.
∵∠BAC=70°,∴∠2=35°.
∵AB是☉O的直径,∴∠ADB=90°.
∴∠B=90°-∠2=55°.
∵A、B、C、D四个点都在☉O上,
∴∠C+∠B=180°.
∴∠C=180°-∠B=125°.
15.解析 (1)如图,连接OA,作OH⊥AC于H,
∵OA2+OC2=8,AC2=8,∴OA2+OC2=AC2,
∴△AOC为直角三角形,
∵OA=OC,∴△AOC为等腰直角三角形,
∵OH⊥AC,∴AH=CH,
∵∠AOC=90°,∴OH=AC=,
即点O到AC的距离为.
(2)由圆周角定理得,∠B=∠AOC=45°,
∵四边形ABCD内接于☉O,
∴∠ADC=180°-45°=135°.
班级 姓名
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
第2课时 圆内接四边形
一、选择题
1. 如图,圆内接四边形ABCD的外角∠ABE为80°,则∠ADC的度数为( )
A.80° B.40° C.100° D.160°
2. 如图,四边形ABCD是☉O的内接四边形,BE是☉O的直径,连接AE.若∠BCD=2∠BAD,则∠DAE的度数是( )
A.30° B.35° C.45° D.60°
3. 如图,四边形ABCD内接于☉O,若∠AOB=40°,BC∥OA,则∠ADC的度数为( )
A.60° B.65° C.70° D.75°
4. 如图,点C,D在以AB为直径的半圆上,且∠ADC=120°,点E是上任意一点,连接BE、CE,则∠BEC的度数为( )
A.20° B.30° C.40° D.60°
5. 如图所示,A、B、C、D四点在☉O上,其中=180°,且=,=.若阿超在上取一点P,在上取一点Q,使得∠APQ=130°,则下列叙述何者正确 ( )
A.Q点在上,且> B.Q点在上,且<
C.Q点在上,且> D.Q点在上,且<
6.如图,四边形ABCD内接于☉O,∠BCD=105°,则∠BOD的度数是( )
A.150° B.120° C.105° D.85°
7.如图,菱形ABCD的顶点B,C,D均在☉A上,点E在弧BD上(不与B、D两点重合),则∠BED的度数为( )
A.90° B.120°
C.135° D.150°
二、填空题
8.如图,在☉O内接四边形ABCD中,若∠ABC=100°,则∠ADC= °.
9.如图,五边形ABCDE的顶点B、C、D、E在☉O上,顶点A在☉O外,且AB=AE.若∠A=100°,则∠CBA+∠CDE= °.
10.如图,四边形ABCD内接于☉O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为 度.
11.如图,四边形ABCD是☉O的内接四边形,∠ADC=150°,弦AC=2,则☉O的半径等于 .
12.如图,点A、B、C、D、E在☉O上,所对的圆心角的度数为30°,则∠E+∠C= .
13.如图,☉O上有两个定点A、B,点P是☉O上一动点(不与A、B两点重合),若∠OAB=35°,则∠APB的度数是 .
三、解答题
14.如图,AB是☉O的直径,点C在☉O上,D是的中点,若∠BAC=70°,求∠C的度数.
15.如图,四边形ABCD内接于☉O,OC=2,AC=2.
(1)求点O到AC的距离;
(2)求∠ADC的度数.
答案全解全析
一、选择题
1.答案 A ∵四边形ABCD为圆内接四边形,∴∠ADC+∠ABC=180°.
∵∠ABE+∠ABC=180°,∴∠ADC=∠ABE=80°.故选A.
2.答案 A ∵四边形ABCD是☉O的内接四边形,
∴∠BCD+∠BAD=180°,
∵∠BCD=2∠BAD,∴∠BCD=120°,∠BAD=60°,
∵BE是☉O的直径,∴∠BAE=90°,
∴∠DAE=90°-∠BAD=90°-60°=30°,故选A.
3.答案 C
∵BC∥OA,∠AOB=40°,∴∠OBC=∠AOB=40°.
∵OA=OB,∠AOB=40°,
∴∠OBA=×(180°-40°)=70°,
∴∠ABC=∠OBA+∠OBC=70°+40°=110°.
∵四边形ABCD内接于☉O,∴∠ADC=180°-∠ABC=180°-110°=70°.故选C.
4.答案 B 如图,连接AC,
∵四边形ABCD为☉O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ABC=180°-120°=60°.
∵AB为直径,
∴∠ACB=90°,∴∠BAC=90°-60°=30°,
∴∠BEC=∠BAC=30°.故选B.
答案 B 连接AD,OB,OC,∵=180°,且=,=,∴∠AOB=∠BOD=90°,∠BOC=∠DOC=45°,如图,在圆周上取一点E,连接AE,CE,则∠AEC=∠AOC=67.5°,易知当Q位于上时,∠APQ≤180°-67.5°=112.5°,∴Q位于上,取的中点F,连接OF,EF,BE,则∠AOF=∠AOB+∠BOF=90°+22.5°=112.5°,
∴∠AEF=∠AOF=56.25°,又易知∠AEB=∠AOB=45°,∴当Q位于上时,∠APQ≤180°-45°=135°且∠APQ≥180°-56.25°=123.75°,∴Q点在上(不含点B与F),则Q点在上,且<.故选B.
6. 答案 A ∵四边形ABCD内接于☉O,∠BCD=105°,
∴∠A=180°-∠BCD=180°-105°=75°.∴∠BOD=2∠A=2×75°=150°.
7. 答案 B 如图,连接AC.∵四边形ABCD是菱形,AB=AC=AD,
∴AB=BC=CD=AD=AC,∴△ABC,△ACD都是等边三角形,
∴∠ACB=∠ACD=60°,∴∠BCD=120°,
∴∠BED=∠BCD=120°.
二、填空题
8.答案 80
解析 ∵四边形ABCD是☉O的内接四边形,∴∠ABC+∠ADC=180°,∴∠ADC=180°-100°=80°.
9.答案 220
解析 如图,连接BE,∵AB=AE,∠A=100°,
∴∠ABE=∠AEB=(180°-∠A)=40°.
∵点B、C、D、E在☉O上,∴∠CDE+∠CBE=180°,
∴∠CBA+∠CDE=∠CDE+∠CBE+∠ABE=180°+40°=220°.
10.答案 45
解析 ∵=,∠BAC=30°,∴∠DCF=∠BAC=30°.∵四边形ABCD是☉O的内接四边形,
∴∠ADC+∠ABC=180°.
∵∠ABC=105°,∴∠ADC=75°,
∴∠E=∠ADC-∠DCF=75°-30°=45°.
11.答案 2
解析 如图,连接OA,OC,∵四边形ABCD是☉O的内接四边形,
∴∠ADC+∠ABC=180°.∵∠ADC=150°,∴∠ABC=30°,∴∠AOC=2∠ABC=60°.∵OA=OC,∴△OAC为等边三角形,∴OA=AC=2,即☉O的半径为2.
12. 答案 165°
解析 如图,连接EA,
∵所对的圆心角的度数为30°,∴∠AEB=15°.
∵四边形ACDE为☉O的内接四边形,
∴∠C+∠AED=180°,
∴∠C+∠BED=180°-15°=165°.
13. 答案 55°或125°
解析 如图,连接OB.当点P在优弧上时,
∵OA=OB,∴∠OBA=∠OAB=35°,
∴∠AOB=110°,
∴∠P=∠AOB=55°;当点P在劣弧上时,如图中点P'所示,∠AP'B=180°-∠APB=125°.
综上,∠APB=55°或125°.
三、解答题
14.解析 如图,连接AD,
在☉O中,∵D是的中点,
∴=,∴∠1=∠2.
∵∠BAC=70°,∴∠2=35°.
∵AB是☉O的直径,∴∠ADB=90°.
∴∠B=90°-∠2=55°.
∵A、B、C、D四个点都在☉O上,
∴∠C+∠B=180°.
∴∠C=180°-∠B=125°.
15.解析 (1)如图,连接OA,作OH⊥AC于H,
∵OA2+OC2=8,AC2=8,∴OA2+OC2=AC2,
∴△AOC为直角三角形,
∵OA=OC,∴△AOC为等腰直角三角形,
∵OH⊥AC,∴AH=CH,
∵∠AOC=90°,∴OH=AC=,
即点O到AC的距离为.
(2)由圆周角定理得,∠B=∠AOC=45°,
∵四边形ABCD内接于☉O,
∴∠ADC=180°-45°=135°.
同课章节目录
