2022-2023学年人教版九年级数学 24.2.2.1直线和圆的位置关系 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学 24.2.2.1直线和圆的位置关系 章节培优训练试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 09:06:57 | ||
图片预览


文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
一、选择题
1. 如图,已知☉O1、☉O2、☉O3、☉O4是四个半径为3的等圆,在这四个圆中,若某圆的圆心到直线l的距离为6,则这个圆是( )
A.☉O1 B.☉O2 C.☉O3 D.☉O4
2. 已知☉O的半径等于5,圆心O到直线l的距离为6,那么直线l与☉O的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
3. 在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆与坐标轴的位置关系为( )
A.与x轴相离,与y轴相切 B.与x轴、y轴都相离
C.与x轴相切,与y轴相离 D.与x轴、y轴都相切
4. 平面内,☉O的半径为1,点P到圆心O的距离为2,过点P可作☉O的切线条数为( )
A.0条 B.1条 C.2条 D.无数条
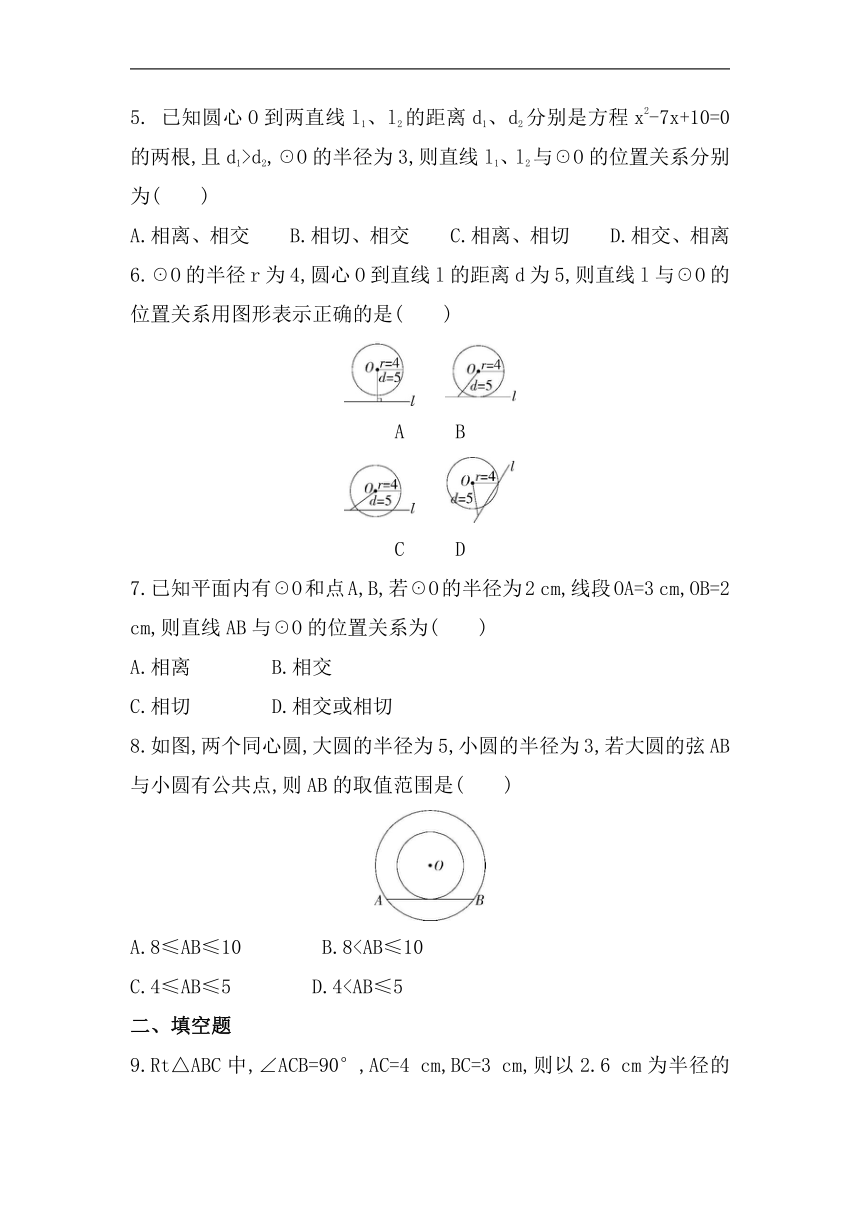
5. 已知圆心O到两直线l1、l2的距离d1、d2分别是方程x2-7x+10=0的两根,且d1>d2,☉O的半径为3,则直线l1、l2与☉O的位置关系分别为( )
A.相离、相交 B.相切、相交 C.相离、相切 D.相交、相离
6.☉O的半径r为4,圆心O到直线l的距离d为5,则直线l与☉O的位置关系用图形表示正确的是( )
A B
C D
7.已知平面内有☉O和点A,B,若☉O的半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB与☉O的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
8.如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则AB的取值范围是( )
A.8≤AB≤10 B.8C.4≤AB≤5 D.4二、填空题
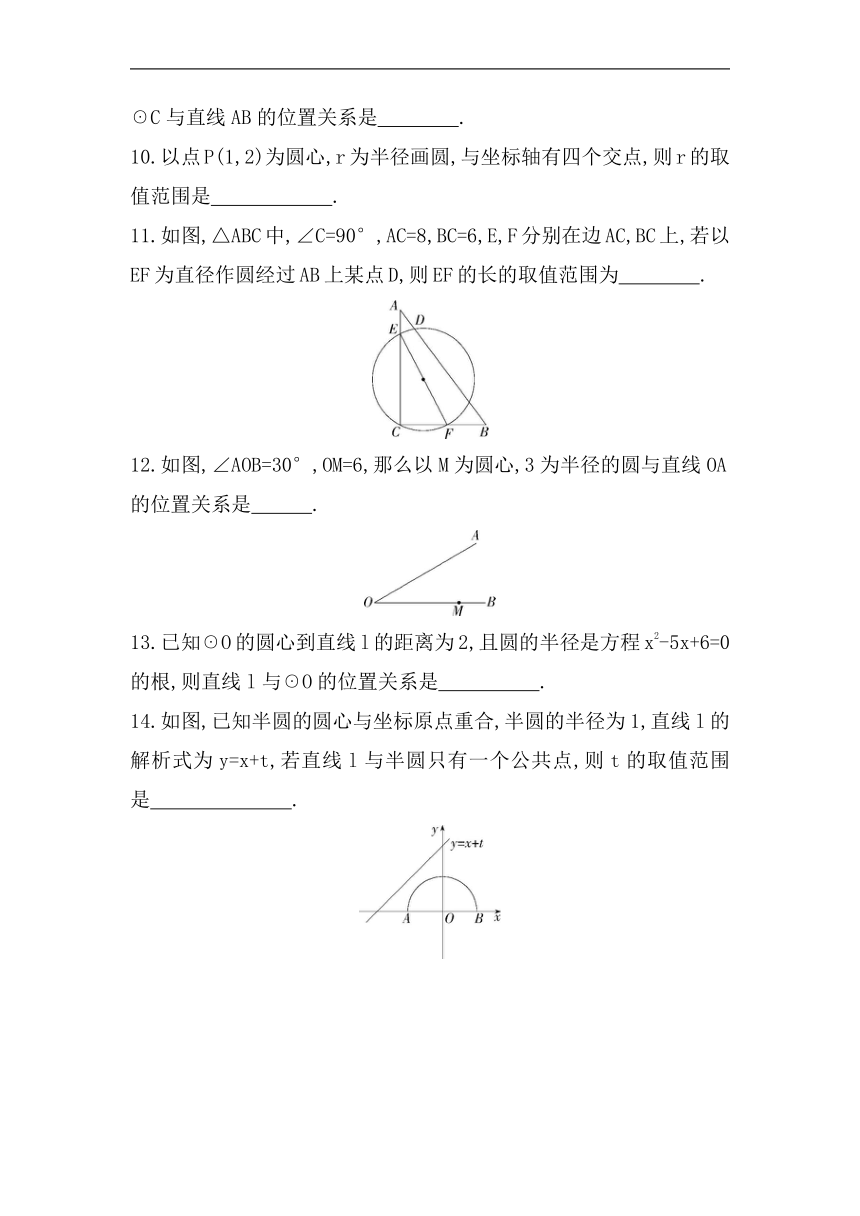
9.Rt△ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,则以2.6 cm为半径的☉C与直线AB的位置关系是 .
10.以点P(1,2)为圆心,r为半径画圆,与坐标轴有四个交点,则r的取值范围是 .
11.如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC上,若以EF为直径作圆经过AB上某点D,则EF的长的取值范围为 .
12.如图,∠AOB=30°,OM=6,那么以M为圆心,3为半径的圆与直线OA的位置关系是 .
13.已知☉O的圆心到直线l的距离为2,且圆的半径是方程x2-5x+6=0的根,则直线l与☉O的位置关系是 .
14.如图,已知半圆的圆心与坐标原点重合,半圆的半径为1,直线l的解析式为y=x+t,若直线l与半圆只有一个公共点,则t的取值范围是 .
三、解答题
15.如图,△ABC中,∠C=90°,AC=3,AB=5,以C为圆心画圆.
(1)当☉C的半径为3.5时,点B与☉C有怎样的位置关系
(2)当☉C与直线AB相交时,求☉C的半径r的取值范围.
答案全解全析
一、选择题
1.答案 B ∵☉O1、☉O2、☉O3、☉O4是四个半径为3的等圆,∴圆心到直线l的距离为6的圆与直线l相离,故选B.
2.答案 A ∵☉O的半径等于5,圆心O到直线l的距离为6,∴直线l和☉O相离,∴直线l与☉O没有公共点.故选A.
3.答案 C ∵1=1,2>1,∴这个圆与x轴相切,与y轴相离.故选C.
4.答案 C ∵☉O的半径为1,点P到圆心O的距离为2,2>1,∴点P与☉O的位置关系是P在☉O外,∵过圆外一点可以作圆的2条切线,∴选C.
5.答案 A ∵d1、d2分别是方程x2-7x+10=0的两根,且d1>d2,
∴d1=5,d2=2,∵☉O的半径为3,∴直线l1、l2与☉O的位置关系分别为相离、相交.故选A.
6. 答案 A 因为圆心O到直线l的距离d为5,☉O的半径r为4,所以直线l与☉O相离,选项A中的图形符合题意.故选A.
7. 答案 D 设圆心O到直线AB的距离为d cm,∵线段OA=3 cm,OB=2 cm,∴d≤2,又☉O的半径为2 cm,∴直线AB与☉O的位置关系为相交或相切.
8. 答案 A 如图,过O点作OC⊥AB于C,连接OA,则AC=BC.当AB与小圆相切时,大圆的弦AB与小圆有唯一公共点,OC取最大值3,此时AC取最小值,为=4,∴AB的最小值为8;当点C与点O重合时,AB最大,AB为大圆的直径,即AB的最大值为10,∴AB的取值范围是8≤AB≤10.
二、填空题
9.答案 相交
解析 如图,过C作CD⊥AB于D,
∵在Rt△ABC中,∠ACB=90°,AC=4 cm,
BC=3 cm,∴由勾股定理得AB=5 cm,
∵由三角形的面积公式得AC·BC=AB·CD,
∴3×4=5CD,∴CD=2.4 cm,
∵2.6>2.4,∴以2.6 cm为半径的☉C与直线AB的位置关系是相交.
10.答案 r>2且r≠
解析 如图,作PA⊥x轴于点A,连接OP,∵点P的坐标为(1,2),
∴OA=1,PA=2,∴OP===,
∴当以点P为圆心,r为半径的圆P与坐标轴有四个交点时,r的取值范围为r>2且r≠.
11.答案 4.8≤EF≤10
解析 ∵∠C=90°,E,F分别在边AC,BC上,∴△ECF是直角三角形,∴点C在以EF为直径的圆上,连接CD,设以EF为直径的圆的圆心为O.当☉O与AB相切且CD⊥AB时,EF取得最小值,此时EF=CD,
∵∠ECF=90°,AC=8,BC=6,∴AB=10,∴EF=CD==4.8;当☉O经过点A、B时,EF取得最大值,此时EF=AB=10.故EF的长的取值范围为4.8≤EF≤10.
12. 答案 相切
解析 如图,过点M作MD⊥AO于点D,
∵∠AOB=30°,OM=6,
∴MD=OM=3,
∴以点M为圆心,3为半径的圆与OA的位置关系是相切.
13. 答案 相切或相交
解析 方程x2-5x+6=0整理得(x-2)(x-3)=0,解得x1=2,x2=3,即圆的半径为2或3,∴当半径为2时,直线l与☉O的位置关系是相切;当半径为3时,直线l与☉O的位置关系是相交.综上所述,直线l与☉O的位置关系是相切或相交.
14. 答案 t=或-1≤t<1
解析 分两种情况:①如图1,直线和半圆相切于点C,此时直线y=x+t与半圆只有一个公共点.连接OC,设直线y=x+t与y轴交于点D,易知∠ODC=45°,∠OCD=90°,由勾股定理得OD=,即t=.②如图2,从直线过点A开始到直线过点B结束的过程中(不包括直线过点A的情况,包括直线过点B的情况),直线y=x+t与半圆只有一个公共点.当直线过点A时,把点A(-1,0)代入直线解析式,得t=1;当直线过点B时,把点B(1,0)代入直线解析式,得t=-1,
∴t的取值范围是-1≤t<1.综上所述,当直线和半圆只有一个公共点时,t=或-1≤t<1.
三、解答题
15.解析 (1)点B在☉C外.
理由如下:
在Rt△ABC中,AC=3,AB=5,
∴BC===4,
∵BC>3.5,即B到圆心C的距离大于☉C的半径,
∴点B在☉C外.
(2)如图,过C作CD⊥AB于D,
则CD===2.4,
当☉C与直线AB相交时,r>2.4.
班级 姓名
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
一、选择题
1. 如图,已知☉O1、☉O2、☉O3、☉O4是四个半径为3的等圆,在这四个圆中,若某圆的圆心到直线l的距离为6,则这个圆是( )
A.☉O1 B.☉O2 C.☉O3 D.☉O4
2. 已知☉O的半径等于5,圆心O到直线l的距离为6,那么直线l与☉O的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
3. 在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆与坐标轴的位置关系为( )
A.与x轴相离,与y轴相切 B.与x轴、y轴都相离
C.与x轴相切,与y轴相离 D.与x轴、y轴都相切
4. 平面内,☉O的半径为1,点P到圆心O的距离为2,过点P可作☉O的切线条数为( )
A.0条 B.1条 C.2条 D.无数条
5. 已知圆心O到两直线l1、l2的距离d1、d2分别是方程x2-7x+10=0的两根,且d1>d2,☉O的半径为3,则直线l1、l2与☉O的位置关系分别为( )
A.相离、相交 B.相切、相交 C.相离、相切 D.相交、相离
6.☉O的半径r为4,圆心O到直线l的距离d为5,则直线l与☉O的位置关系用图形表示正确的是( )
A B
C D
7.已知平面内有☉O和点A,B,若☉O的半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB与☉O的位置关系为( )
A.相离 B.相交
C.相切 D.相交或相切
8.如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则AB的取值范围是( )
A.8≤AB≤10 B.8
9.Rt△ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,则以2.6 cm为半径的☉C与直线AB的位置关系是 .
10.以点P(1,2)为圆心,r为半径画圆,与坐标轴有四个交点,则r的取值范围是 .
11.如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC上,若以EF为直径作圆经过AB上某点D,则EF的长的取值范围为 .
12.如图,∠AOB=30°,OM=6,那么以M为圆心,3为半径的圆与直线OA的位置关系是 .
13.已知☉O的圆心到直线l的距离为2,且圆的半径是方程x2-5x+6=0的根,则直线l与☉O的位置关系是 .
14.如图,已知半圆的圆心与坐标原点重合,半圆的半径为1,直线l的解析式为y=x+t,若直线l与半圆只有一个公共点,则t的取值范围是 .
三、解答题
15.如图,△ABC中,∠C=90°,AC=3,AB=5,以C为圆心画圆.
(1)当☉C的半径为3.5时,点B与☉C有怎样的位置关系
(2)当☉C与直线AB相交时,求☉C的半径r的取值范围.
答案全解全析
一、选择题
1.答案 B ∵☉O1、☉O2、☉O3、☉O4是四个半径为3的等圆,∴圆心到直线l的距离为6的圆与直线l相离,故选B.
2.答案 A ∵☉O的半径等于5,圆心O到直线l的距离为6,∴直线l和☉O相离,∴直线l与☉O没有公共点.故选A.
3.答案 C ∵1=1,2>1,∴这个圆与x轴相切,与y轴相离.故选C.
4.答案 C ∵☉O的半径为1,点P到圆心O的距离为2,2>1,∴点P与☉O的位置关系是P在☉O外,∵过圆外一点可以作圆的2条切线,∴选C.
5.答案 A ∵d1、d2分别是方程x2-7x+10=0的两根,且d1>d2,
∴d1=5,d2=2,∵☉O的半径为3,∴直线l1、l2与☉O的位置关系分别为相离、相交.故选A.
6. 答案 A 因为圆心O到直线l的距离d为5,☉O的半径r为4,所以直线l与☉O相离,选项A中的图形符合题意.故选A.
7. 答案 D 设圆心O到直线AB的距离为d cm,∵线段OA=3 cm,OB=2 cm,∴d≤2,又☉O的半径为2 cm,∴直线AB与☉O的位置关系为相交或相切.
8. 答案 A 如图,过O点作OC⊥AB于C,连接OA,则AC=BC.当AB与小圆相切时,大圆的弦AB与小圆有唯一公共点,OC取最大值3,此时AC取最小值,为=4,∴AB的最小值为8;当点C与点O重合时,AB最大,AB为大圆的直径,即AB的最大值为10,∴AB的取值范围是8≤AB≤10.
二、填空题
9.答案 相交
解析 如图,过C作CD⊥AB于D,
∵在Rt△ABC中,∠ACB=90°,AC=4 cm,
BC=3 cm,∴由勾股定理得AB=5 cm,
∵由三角形的面积公式得AC·BC=AB·CD,
∴3×4=5CD,∴CD=2.4 cm,
∵2.6>2.4,∴以2.6 cm为半径的☉C与直线AB的位置关系是相交.
10.答案 r>2且r≠
解析 如图,作PA⊥x轴于点A,连接OP,∵点P的坐标为(1,2),
∴OA=1,PA=2,∴OP===,
∴当以点P为圆心,r为半径的圆P与坐标轴有四个交点时,r的取值范围为r>2且r≠.
11.答案 4.8≤EF≤10
解析 ∵∠C=90°,E,F分别在边AC,BC上,∴△ECF是直角三角形,∴点C在以EF为直径的圆上,连接CD,设以EF为直径的圆的圆心为O.当☉O与AB相切且CD⊥AB时,EF取得最小值,此时EF=CD,
∵∠ECF=90°,AC=8,BC=6,∴AB=10,∴EF=CD==4.8;当☉O经过点A、B时,EF取得最大值,此时EF=AB=10.故EF的长的取值范围为4.8≤EF≤10.
12. 答案 相切
解析 如图,过点M作MD⊥AO于点D,
∵∠AOB=30°,OM=6,
∴MD=OM=3,
∴以点M为圆心,3为半径的圆与OA的位置关系是相切.
13. 答案 相切或相交
解析 方程x2-5x+6=0整理得(x-2)(x-3)=0,解得x1=2,x2=3,即圆的半径为2或3,∴当半径为2时,直线l与☉O的位置关系是相切;当半径为3时,直线l与☉O的位置关系是相交.综上所述,直线l与☉O的位置关系是相切或相交.
14. 答案 t=或-1≤t<1
解析 分两种情况:①如图1,直线和半圆相切于点C,此时直线y=x+t与半圆只有一个公共点.连接OC,设直线y=x+t与y轴交于点D,易知∠ODC=45°,∠OCD=90°,由勾股定理得OD=,即t=.②如图2,从直线过点A开始到直线过点B结束的过程中(不包括直线过点A的情况,包括直线过点B的情况),直线y=x+t与半圆只有一个公共点.当直线过点A时,把点A(-1,0)代入直线解析式,得t=1;当直线过点B时,把点B(1,0)代入直线解析式,得t=-1,
∴t的取值范围是-1≤t<1.综上所述,当直线和半圆只有一个公共点时,t=或-1≤t<1.
三、解答题
15.解析 (1)点B在☉C外.
理由如下:
在Rt△ABC中,AC=3,AB=5,
∴BC===4,
∵BC>3.5,即B到圆心C的距离大于☉C的半径,
∴点B在☉C外.
(2)如图,过C作CD⊥AB于D,
则CD===2.4,
当☉C与直线AB相交时,r>2.4.
同课章节目录
