2022-2023学年人教版九年级数学上册24.2.2.2切线的判定与性质 章节培优训练试卷(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册24.2.2.2切线的判定与性质 章节培优训练试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 379.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 09:08:21 | ||
图片预览




文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系
第2课时 切线的判定与性质
一、选择题
1.如图,AB是☉O的直径,BC是☉O的切线,若∠BAC=35°,则∠ACB的大小为( )
A.35° B.45° C.55° D.65°
2.如图,BC为☉O的直径,弦AD⊥BC于点E,直线l切☉O于点C,延长OD交l于点F,若AE=2,∠ABC=22.5°,则CF的长为( )
A.2 B.2 C.2 D.4
3.如图,∠ABC=70°,O为射线BC上一点,以点O为圆心,OB长为半径作☉O,要使射线BA与☉O相切,应将射线绕点B按顺时针方向旋转( )
A.35°或70° B.40°或100°
C.40°或90° D.50°或110°
如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,
∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
5.如图,点A在☉O上,点B在☉O外,以下条件能判定AB是☉O切线的有( )
①∠O+∠B=90°;②∠A-∠B=∠O;③OB=AB=OA;④OA∶AB∶OB=3∶4∶5.
A.1个 B.2个
C.3个 D.4个
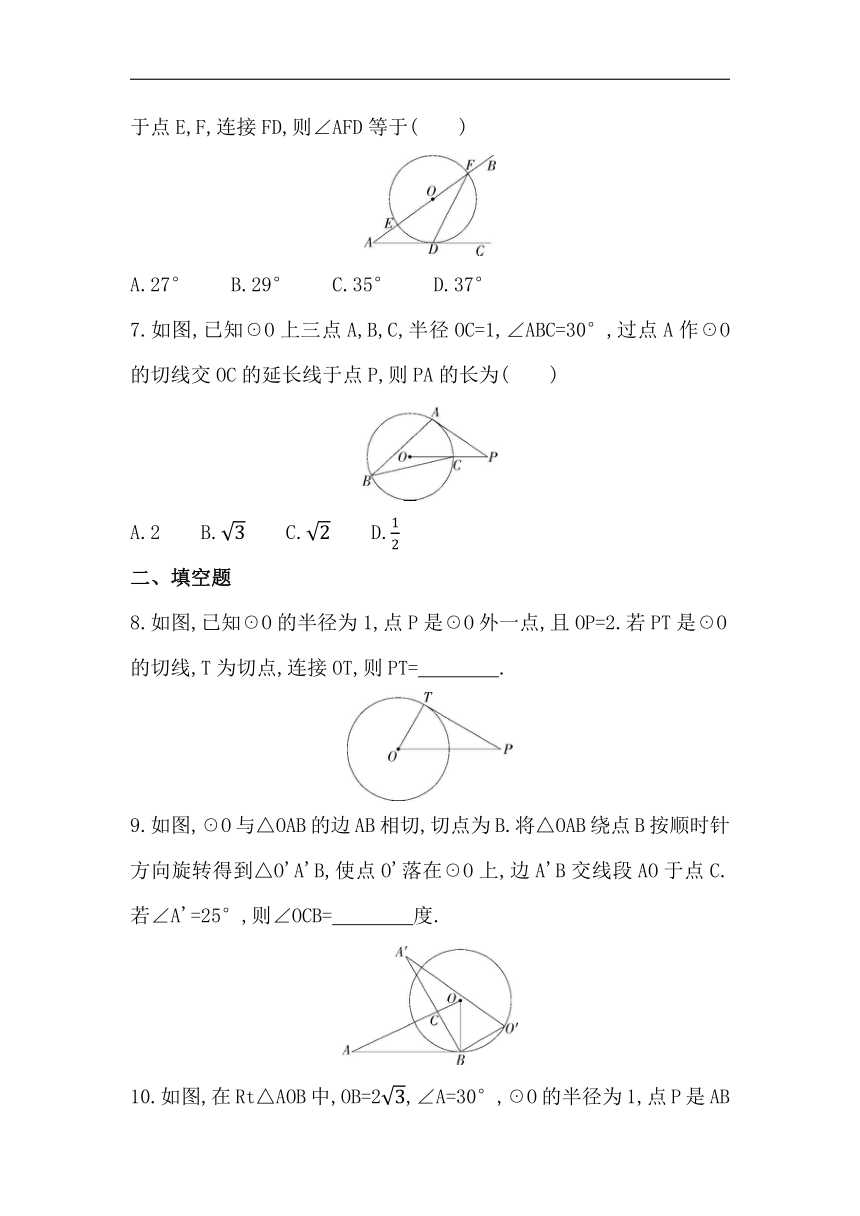
6.如图,∠BAC=36°,点O在边AB上,☉O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )
A.27° B.29° C.35° D.37°
7.如图,已知☉O上三点A,B,C,半径OC=1,∠ABC=30°,过点A作☉O的切线交OC的延长线于点P,则PA的长为( )
A.2 B. C. D.
二、填空题
8.如图,已知☉O的半径为1,点P是☉O外一点,且OP=2.若PT是☉O的切线,T为切点,连接OT,则PT= .
9.如图,☉O与△OAB的边AB相切,切点为B.将△OAB绕点B按顺时针方向旋转得到△O'A'B,使点O'落在☉O上,边A'B交线段AO于点C.若∠A'=25°,则∠OCB= 度.
10.如图,在Rt△AOB中,OB=2,∠A=30°,☉O的半径为1,点P是AB边上的动点,过点P作☉O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 .
三、解答题
11.如图,AB为☉O的直径,点C,D在☉O上,==,DE⊥AC.
求证:DE是☉O的切线.
12.如图,OA=OB=13 cm,AB=24 cm,☉O的直径为10 cm.求证:AB是☉O的切线.
13.如图,在Rt△ABC中,∠C=90°,以BC为直径的☉O交斜边AB于点D,若E是AC的中点,连接DE.求证:DE为☉O的切线.
14.如图,AB是☉O的直径,==2,连接AC、CD、AD,CD交AB于点F,过点B作☉O的切线BM交AD的延长线于点E.
(1)求证:AC=CD;
(2)连接OE,若DE=2,求OE的长.
答案全解全析
一、选择题
1.答案 C ∵BC是☉O的切线,AB是☉O的直径,
∴AB⊥BC,
∴∠ABC=90°,
∴∠ACB=90°-∠BAC=90°-35°=55°.故选C.
2.答案 B ∵BC为☉O的直径,弦AD⊥BC于点E,AE=2,∠ABC=22.5°,
∴∠COD=2∠ABC=45°,DE=AE=2,
∴OE=ED=2,
∴OC=OD=2.
∵直线l切☉O于点C,
∴BC⊥CF,∴△OCF是等腰直角三角形,
∴CF=OC=2.故选B.
答案 B 设旋转后与☉O相切于点D,连接OD,∴OD⊥BD,∴∠ODB=90°,
∵OD=OB,∴∠OBD=30°,如图,当点D在射线BC上方时,D在D1处,∠ABD1=∠ABC-∠OBD1=70°-30°=40°;当点D在射线BC下方时,
D在D2处,∠ABD2=∠ABC+∠OBD2=70°+30°=100°.故选B.
答案 B 如图,连接AD,∵BC与☉A相切于点D,
∴AD⊥BC,∴∠ADB=∠ADC=90°,
∵AB=6,AG=AD=3,∴AD=AB,∴∠B=30°,
∴∠GAD=60°,∵∠CDE=18°,
∴∠ADE=90°-18°=72°,
∵AD=AE,∴∠AED=∠ADE=72°,
∴∠DAE=180°-∠ADE-∠AED=180°-72°-72°=36°,
∴∠BAC=∠BAD+∠CAD=60°+36°=96°,
∴∠GFE=∠GAE=×96°=48°,故选B.
5. 答案 D ①∵∠O+∠B=90°,∴∠A=90°,∴AB是☉O的切线;
②∵∠A-∠B=∠O,∴∠A=∠O+∠B=×180°=90°,∴AB是☉O的切线;
③∵OB=AB=OA,∴OA2+AB2=OB2,∴∠A=90°,∴AB是☉O的切线;
④∵OA∶AB∶OB=3∶4∶5,设OA=3x,则AB=4x,OB=5x,
∴OA2+AB2=9x2+16x2=25x2,OB2=25x2,∴OA2+AB2=OB2,∴∠A=90°,∴AB是☉O的切线.综上所述,①②③④都能判定AB是☉O的切线.
6. 答案 A 如图,连接OD,∵☉O与边AC相切于点D,
∴∠ADO=90°,
∵∠BAC=36°,
∴∠AOD=90°-36°=54°,
∵OD=OF,∴∠AFD=∠ODF,
∴∠AFD=∠AOD=×54°=27°.
7. 答案 B 如图,连接OA,
∵∠ABC=30°,∴∠AOC=2∠ABC=60°.
∵AP为☉O的切线,
∴∠OAP=90°,∴∠P=30°.
∵OA=OC=1,∴OP=2,∴AP=.故选B.
二、填空题
8.答案
解析 ∵PT是☉O的切线,T为切点,∴OT⊥PT,在Rt△OPT中,OT=1,OP=2,∴PT===,故PT=.
9.答案 85
解析 ∵☉O与△OAB的边AB相切,∴OB⊥AB,∴∠OBA=90°,连接OO',如图,∵△OAB绕点B按顺时针方向旋转得到△O'A'B,
∴∠A=∠A'=25°,∠ABA'=∠OBO',BO=BO',∵OB=OO',∴△OO'B为等边三角形,∴∠OBO'=60°,∴∠ABA'=60°,∴∠OCB=∠A+∠ABC=25°+60°=85°.
10.答案 2
解析 如图,连接OP、OQ,作OP'⊥AB于P',∵PQ是☉O的切线,∴OQ⊥PQ,
∴PQ==,当OP的长度最小时,线段PQ的长度最小,当OP⊥AB时,OP的长度最小,在Rt△AOB中,∠A=30°,OB=2,∴AB=4,由勾股定理可得OA=6.在Rt△AOP'中,∠A=30°,∴OP'=OA=3,∴线段PQ长度的最小值==2.
三、解答题
11.证明 如图,连接OD,
∵==,
∴∠BOD=×180°=60°.
∵=,∴∠EAD=∠DAB=∠BOD=30°.
∵OA=OD,∴∠ADO=∠DAB=30°.
∵DE⊥AC,∴∠E=90°,
∴∠EAD+∠EDA=90°,
∴∠EDA=60°,
∴∠EDO=∠EDA+∠ADO=90°,
∴OD⊥DE.
∵OD是☉O的半径,
∴DE是☉O的切线.
12.证明 如图,过点O作OC⊥AB于点C,
∵OA=OB=13 cm,AB=24 cm,
∴AC=AB=12(cm).
在Rt△OAC中,根据勾股定理,得
OC==5(cm).
∵☉O的直径为10 cm
∴☉O的半径r为5 cm,
∴OC=r,即OC为☉O的半径,
∵OC⊥AB,∴AB是☉O的切线.
13.证明 如图,连接OD、OE,
∵BC是☉O的直径,E是AC的中点,
∴OE是△ABC的中位线,∴OE∥AB,
∴∠EOD=∠ODB,∠EOC=∠B.
又∵OB=OD,∴∠B=∠ODB,
∴∠EOD=∠EOC.
又∵OC=OD,OE=OE,
∴△EOD≌△EOC,
∴∠EDO=∠ECO.
又∵∠ACB=90°,∴∠EDO=90°.
又∵点D在☉O上,
∴DE为☉O的切线.
14.解析 (1)证明:∵==2,
∴AD=CD,B是的中点.
∵AB是直径,
∴=,
∴AD=AC,
∴AC=CD.
(2)如图,连接BD,
∵AD=DC=AC,
∴∠ADC=∠DAC=60°.
∵=2,∴=,∴∠DAB=∠CAB,∴∠DAB=∠DAC=30°.
∵BM切☉O于点B,AB是直径,
∴BM⊥AB,
∵CD⊥AB,∴BM∥CD,
∴∠AEB=∠ADC=60°,
∵AB是直径,∴∠ADB=90°,∴∠BDE=90°.
在Rt△BDE中,∵∠DBE=90°-∠DEB=30°,
∴BE=2DE=4,
∴BD===2.
在Rt△BDA中,∵∠DAB=30°,
∴AB=2BD=4,
∴OB=AB=2,
在Rt△OBE中,OE===2.
班级 姓名
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系
第2课时 切线的判定与性质
一、选择题
1.如图,AB是☉O的直径,BC是☉O的切线,若∠BAC=35°,则∠ACB的大小为( )
A.35° B.45° C.55° D.65°
2.如图,BC为☉O的直径,弦AD⊥BC于点E,直线l切☉O于点C,延长OD交l于点F,若AE=2,∠ABC=22.5°,则CF的长为( )
A.2 B.2 C.2 D.4
3.如图,∠ABC=70°,O为射线BC上一点,以点O为圆心,OB长为半径作☉O,要使射线BA与☉O相切,应将射线绕点B按顺时针方向旋转( )
A.35°或70° B.40°或100°
C.40°或90° D.50°或110°
如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,
∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
5.如图,点A在☉O上,点B在☉O外,以下条件能判定AB是☉O切线的有( )
①∠O+∠B=90°;②∠A-∠B=∠O;③OB=AB=OA;④OA∶AB∶OB=3∶4∶5.
A.1个 B.2个
C.3个 D.4个
6.如图,∠BAC=36°,点O在边AB上,☉O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )
A.27° B.29° C.35° D.37°
7.如图,已知☉O上三点A,B,C,半径OC=1,∠ABC=30°,过点A作☉O的切线交OC的延长线于点P,则PA的长为( )
A.2 B. C. D.
二、填空题
8.如图,已知☉O的半径为1,点P是☉O外一点,且OP=2.若PT是☉O的切线,T为切点,连接OT,则PT= .
9.如图,☉O与△OAB的边AB相切,切点为B.将△OAB绕点B按顺时针方向旋转得到△O'A'B,使点O'落在☉O上,边A'B交线段AO于点C.若∠A'=25°,则∠OCB= 度.
10.如图,在Rt△AOB中,OB=2,∠A=30°,☉O的半径为1,点P是AB边上的动点,过点P作☉O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 .
三、解答题
11.如图,AB为☉O的直径,点C,D在☉O上,==,DE⊥AC.
求证:DE是☉O的切线.
12.如图,OA=OB=13 cm,AB=24 cm,☉O的直径为10 cm.求证:AB是☉O的切线.
13.如图,在Rt△ABC中,∠C=90°,以BC为直径的☉O交斜边AB于点D,若E是AC的中点,连接DE.求证:DE为☉O的切线.
14.如图,AB是☉O的直径,==2,连接AC、CD、AD,CD交AB于点F,过点B作☉O的切线BM交AD的延长线于点E.
(1)求证:AC=CD;
(2)连接OE,若DE=2,求OE的长.
答案全解全析
一、选择题
1.答案 C ∵BC是☉O的切线,AB是☉O的直径,
∴AB⊥BC,
∴∠ABC=90°,
∴∠ACB=90°-∠BAC=90°-35°=55°.故选C.
2.答案 B ∵BC为☉O的直径,弦AD⊥BC于点E,AE=2,∠ABC=22.5°,
∴∠COD=2∠ABC=45°,DE=AE=2,
∴OE=ED=2,
∴OC=OD=2.
∵直线l切☉O于点C,
∴BC⊥CF,∴△OCF是等腰直角三角形,
∴CF=OC=2.故选B.
答案 B 设旋转后与☉O相切于点D,连接OD,∴OD⊥BD,∴∠ODB=90°,
∵OD=OB,∴∠OBD=30°,如图,当点D在射线BC上方时,D在D1处,∠ABD1=∠ABC-∠OBD1=70°-30°=40°;当点D在射线BC下方时,
D在D2处,∠ABD2=∠ABC+∠OBD2=70°+30°=100°.故选B.
答案 B 如图,连接AD,∵BC与☉A相切于点D,
∴AD⊥BC,∴∠ADB=∠ADC=90°,
∵AB=6,AG=AD=3,∴AD=AB,∴∠B=30°,
∴∠GAD=60°,∵∠CDE=18°,
∴∠ADE=90°-18°=72°,
∵AD=AE,∴∠AED=∠ADE=72°,
∴∠DAE=180°-∠ADE-∠AED=180°-72°-72°=36°,
∴∠BAC=∠BAD+∠CAD=60°+36°=96°,
∴∠GFE=∠GAE=×96°=48°,故选B.
5. 答案 D ①∵∠O+∠B=90°,∴∠A=90°,∴AB是☉O的切线;
②∵∠A-∠B=∠O,∴∠A=∠O+∠B=×180°=90°,∴AB是☉O的切线;
③∵OB=AB=OA,∴OA2+AB2=OB2,∴∠A=90°,∴AB是☉O的切线;
④∵OA∶AB∶OB=3∶4∶5,设OA=3x,则AB=4x,OB=5x,
∴OA2+AB2=9x2+16x2=25x2,OB2=25x2,∴OA2+AB2=OB2,∴∠A=90°,∴AB是☉O的切线.综上所述,①②③④都能判定AB是☉O的切线.
6. 答案 A 如图,连接OD,∵☉O与边AC相切于点D,
∴∠ADO=90°,
∵∠BAC=36°,
∴∠AOD=90°-36°=54°,
∵OD=OF,∴∠AFD=∠ODF,
∴∠AFD=∠AOD=×54°=27°.
7. 答案 B 如图,连接OA,
∵∠ABC=30°,∴∠AOC=2∠ABC=60°.
∵AP为☉O的切线,
∴∠OAP=90°,∴∠P=30°.
∵OA=OC=1,∴OP=2,∴AP=.故选B.
二、填空题
8.答案
解析 ∵PT是☉O的切线,T为切点,∴OT⊥PT,在Rt△OPT中,OT=1,OP=2,∴PT===,故PT=.
9.答案 85
解析 ∵☉O与△OAB的边AB相切,∴OB⊥AB,∴∠OBA=90°,连接OO',如图,∵△OAB绕点B按顺时针方向旋转得到△O'A'B,
∴∠A=∠A'=25°,∠ABA'=∠OBO',BO=BO',∵OB=OO',∴△OO'B为等边三角形,∴∠OBO'=60°,∴∠ABA'=60°,∴∠OCB=∠A+∠ABC=25°+60°=85°.
10.答案 2
解析 如图,连接OP、OQ,作OP'⊥AB于P',∵PQ是☉O的切线,∴OQ⊥PQ,
∴PQ==,当OP的长度最小时,线段PQ的长度最小,当OP⊥AB时,OP的长度最小,在Rt△AOB中,∠A=30°,OB=2,∴AB=4,由勾股定理可得OA=6.在Rt△AOP'中,∠A=30°,∴OP'=OA=3,∴线段PQ长度的最小值==2.
三、解答题
11.证明 如图,连接OD,
∵==,
∴∠BOD=×180°=60°.
∵=,∴∠EAD=∠DAB=∠BOD=30°.
∵OA=OD,∴∠ADO=∠DAB=30°.
∵DE⊥AC,∴∠E=90°,
∴∠EAD+∠EDA=90°,
∴∠EDA=60°,
∴∠EDO=∠EDA+∠ADO=90°,
∴OD⊥DE.
∵OD是☉O的半径,
∴DE是☉O的切线.
12.证明 如图,过点O作OC⊥AB于点C,
∵OA=OB=13 cm,AB=24 cm,
∴AC=AB=12(cm).
在Rt△OAC中,根据勾股定理,得
OC==5(cm).
∵☉O的直径为10 cm
∴☉O的半径r为5 cm,
∴OC=r,即OC为☉O的半径,
∵OC⊥AB,∴AB是☉O的切线.
13.证明 如图,连接OD、OE,
∵BC是☉O的直径,E是AC的中点,
∴OE是△ABC的中位线,∴OE∥AB,
∴∠EOD=∠ODB,∠EOC=∠B.
又∵OB=OD,∴∠B=∠ODB,
∴∠EOD=∠EOC.
又∵OC=OD,OE=OE,
∴△EOD≌△EOC,
∴∠EDO=∠ECO.
又∵∠ACB=90°,∴∠EDO=90°.
又∵点D在☉O上,
∴DE为☉O的切线.
14.解析 (1)证明:∵==2,
∴AD=CD,B是的中点.
∵AB是直径,
∴=,
∴AD=AC,
∴AC=CD.
(2)如图,连接BD,
∵AD=DC=AC,
∴∠ADC=∠DAC=60°.
∵=2,∴=,∴∠DAB=∠CAB,∴∠DAB=∠DAC=30°.
∵BM切☉O于点B,AB是直径,
∴BM⊥AB,
∵CD⊥AB,∴BM∥CD,
∴∠AEB=∠ADC=60°,
∵AB是直径,∴∠ADB=90°,∴∠BDE=90°.
在Rt△BDE中,∵∠DBE=90°-∠DEB=30°,
∴BE=2DE=4,
∴BD===2.
在Rt△BDA中,∵∠DAB=30°,
∴AB=2BD=4,
∴OB=AB=2,
在Rt△OBE中,OE===2.
同课章节目录
