(2022秋季新教材)人教版 六年级数学上册6.4 解决问题课件(共31页PPT)
文档属性
| 名称 | (2022秋季新教材)人教版 六年级数学上册6.4 解决问题课件(共31页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 08:47:14 | ||
图片预览










文档简介
(共31张PPT)
2
0
2
2
2022秋人教版数学六年级上册
人教版 六年级上册
第6单元 百分数(一)
第 4 课时 解决问题(1)
1、把下面各数化成百分数。
0.63 1.08 7 0.044
2、说说下面每个百分数的具体含义。
(1)某种花生的出油率是35%。
(2)实际用电量占计划用电量的80%。
(3)李庄今年荔枝产量是去年的120%。
1
4
7
20
3
5
5
8
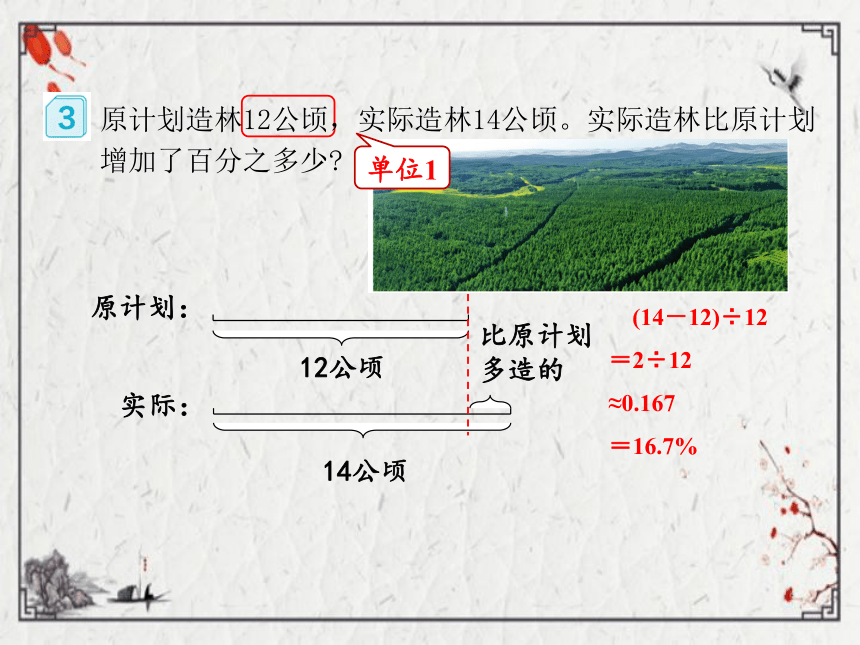
单位1
原计划:
12公顷
实际:
14公顷
比原计划多造的
(14-12)÷12
=2÷12
≈0.167
=16.7%
原计划造林12公顷,实际造林14公顷。实际造林比原计划增加了百分之多少
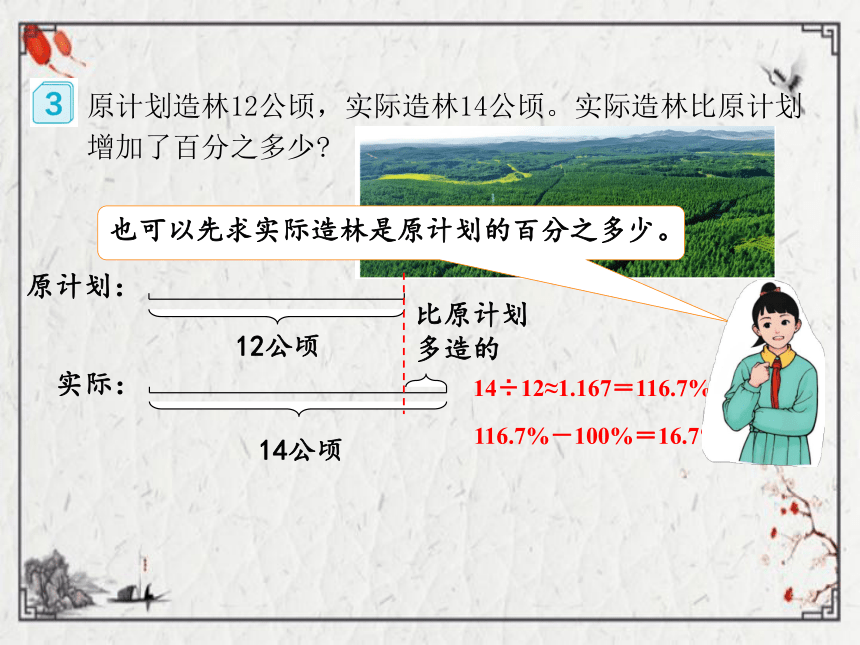
原计划造林12公顷,实际造林14公顷。实际造林比原计划增加了百分之多少
14÷12≈1.167=116.7%
原计划:
12公顷
实际:
14公顷
比原计划多造的
也可以先求实际造林是原计划的百分之多少。
116.7%-100%=16.7%
(14-12)÷12
=2÷12
≈0.167
=16.7%
14÷12≈1.167=116.7%
116.7%-100%=16.7%
答:实际造林比原来增加了16.7%。
原计划造林12公顷,实际造林14公顷。实际造林比原计划增加了百分之多少
(14-12)÷14
=2÷14
≈ 0.143
=14.3%
原计划造林12公顷,实际造林14公顷。原计划造林比实际造林减少了( )%。
你会解答吗?
为什么除以14?
14.3
“求一个数比另一个数多(或少)百分之几”的解题方法:
方法一:先求一个数比另一个数多(或少)的具体量,再除以单位“1”的量,即两数差量÷单位“1”的量;
方法二:把另一个数看成单位“1”,即100%,先求一个数是另一个数的百分之几,再根据所求问题把两个百分数相减。
在实际生活中,人们常用“增加百分之几”“减少百分之几”“节约百分之几”……来表示增加、减少的幅度。
你知道上面这些话的含义吗?举例说一说。
解答“谁比谁多百分之几”的问题的解题关键是什么?
弄懂问题是求哪部分数占单位“1”的百分之几,找准单位“1”。
课堂讨论:
说一说:
下列句子是求谁占谁的百分之几?哪个量是单位“1”?
①今年产量比去年多百分之几?
③彩电降价了百分之几?
②这个月用电比上个月节约了百分之几?
(和去年比较,去年产量是单位“1”)
(和上个月比较,上个月用电量是单位“1”)
(现价和原价比较,原价是单位“1”)
1、小飞家原来每月用水约10t,更换了节水龙头后
每月用水约9t,每月用水比原来节约了百分之几?
(10-9)÷10
=1÷10
=10%
答:每月用水比原来节约了10%。
求现在每月用水比原来节约了百分之几,就是求现在每月比原来每月少用的用水量是原来每月用水量的百分之几。原来每月的用水量是单位“1”。
①80千克比50千克多( )千克,
多( )%。
②50千克比80千克少( )千克,
少( )%。
③50千克是80千克的( )%。
④80千克是50千克的( )%。
2、填一填
30
60
30
37.5
62.5
160
①一个足球运动员,经训练速度提高了2%米。( )
②甲数比乙数多10%,乙数就比甲数少10%。 ( )
③王师傅生产了100个零件,结果98个零件合格,合格的零件占生产零件总数的98%。 ( )
×
×
√
3、判断。
4、姐姐身高150厘米,比弟弟高10厘米。求姐姐比弟弟
高百分之几的算式是( )。
①10÷150 ②10÷(150-10)
③(150-10)÷150 ④10÷(150+10)
正确答案选②。
不要认为降低百分之几,提高百分之几……一定要用一个数减去另一个数的差除以标准量,应仔细审题,如果解题时所需数量给出,就直接使用。
同学们,这节课你都学到了什么?
求一个数比另一个数多(或少)百分之几
求一个数比另一个数多(或少)百分之几,可以先求多(或少)的部分,再求多(或少)的部分是另一个数的百分之几;也可以先求一个数是另外一个数的百分之几,再求比另外一个数多(或少)百分之几。
人教版 六年级上册
第6单元 百分数(一)
第 5 课时 解决问题(2)
1、为了缓解交通拥挤的状况,某市正在进行道路拓宽。
团结路的路宽由原来的12m增加到25m,拓宽了百
分之几?
(25-12)÷12
=13÷12
≈ 108.3%
答:拓宽了108.3%。
求拓宽了百分之几,就是求现在的路宽比原来的路宽多出来的宽度是原来路宽的百分之几。原来的路宽是单位“1”。
2、六年级学生去植树,男生植树320棵,比女生多20%,比女生多植了多少棵?
例4:学校图书室原有图书1400册,今年图书册数增加了12%。现在图书室有多少册图书?
已知条件 原有图书1400册,今年图书册数增加了12%。
所求问题
现在图书室有多少册图书?
分析信息:
例4:学校图书室原有图书1400册,今年图书册数增加了12%。现在图书室有多少册图书?
把原来图书总册数看作单位“1”。
1400×12%=168(册)
1400+168=1568(册)
答:现在图书室有1568册图书。
1400×(1+12%)
=1400×112%
=1568(册)
方法一:先求出今年比去年增加的图书册数,再加上原有的册数就是今年的册数。
方法二: 先求出今年图书册数是原有图书册数的百分之几,再求出今年的册数。
探索新知
做一做:
龙泉镇去年有小学生2800人,今年比去年减少了
0.5%。今年有小学生多少人?
方法一:
2800-2800×0.5%
=2800-14
=2786(人)
答:今年有小学生2786人。
方法二:
2800×(1-0.5%)
=2800×99.5%
=2786(人)
答:今年有小学生2786人。
怎样求比一个数多(或少)百分之几的数是多少?
小结:
求比一个数多(或少)百分之几的数是多少与求比一个数多(或少)几分之几的思路相同;
方法一是先求多(或少)的数;
方法二是先求要求的数是这个数的百分之几。
小组讨论:
1、一个工厂由于采用了新工艺,现在每件产品成本是37.4元,比原来降低了15%。原来每件产品的成本是多少元?
单位“1”
现成本﹦原成本-降低的成本
(原成本×15%)
解:设原来每件成本x元。
x-15%x=37.4
算术方法解:
数量÷对应分率=单位“1”的量
单位“1”的量未知,可用方程解答。
37.4
(1-15%)
现成本
现成本占单位“1”的百分率
÷
巩固拓展
想一想,还可以怎样做?
2.袁隆平院士是我国著名科学家,被誉为“杂交水稻之父”。2021年,袁隆平院士指导的杂交水稻示范片双季稻年平均产量达到了每公顷24.06t,比攻关目标高了约7 % 。攻关目标约是每公顷多少吨 ( 得数保留一位小数。)
解:设2021年全国平均每公顷水稻产量大约是xt。
(1+7%)x=24.06
1.07x=24.06
x=24.06÷1.07
x≈22.49
答:2021年全国平均每公顷水稻产量大约是7.57吨。
同学们,这节课你都学到了什么?
百分数应用题的解题思路和分数应用题的相同。
1、单位“1”的量已知,根据求一个数的几分之几是多少用乘法计算。
2、单位“1”的量未知,可根据等量关系列方程或用除法计算。
关键是找准单位“1”。
数量÷对应分率=单位“1”的对应量
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2
0
2
2
2022秋人教版数学六年级上册
人教版 六年级上册
第6单元 百分数(一)
第 4 课时 解决问题(1)
1、把下面各数化成百分数。
0.63 1.08 7 0.044
2、说说下面每个百分数的具体含义。
(1)某种花生的出油率是35%。
(2)实际用电量占计划用电量的80%。
(3)李庄今年荔枝产量是去年的120%。
1
4
7
20
3
5
5
8
单位1
原计划:
12公顷
实际:
14公顷
比原计划多造的
(14-12)÷12
=2÷12
≈0.167
=16.7%
原计划造林12公顷,实际造林14公顷。实际造林比原计划增加了百分之多少
原计划造林12公顷,实际造林14公顷。实际造林比原计划增加了百分之多少
14÷12≈1.167=116.7%
原计划:
12公顷
实际:
14公顷
比原计划多造的
也可以先求实际造林是原计划的百分之多少。
116.7%-100%=16.7%
(14-12)÷12
=2÷12
≈0.167
=16.7%
14÷12≈1.167=116.7%
116.7%-100%=16.7%
答:实际造林比原来增加了16.7%。
原计划造林12公顷,实际造林14公顷。实际造林比原计划增加了百分之多少
(14-12)÷14
=2÷14
≈ 0.143
=14.3%
原计划造林12公顷,实际造林14公顷。原计划造林比实际造林减少了( )%。
你会解答吗?
为什么除以14?
14.3
“求一个数比另一个数多(或少)百分之几”的解题方法:
方法一:先求一个数比另一个数多(或少)的具体量,再除以单位“1”的量,即两数差量÷单位“1”的量;
方法二:把另一个数看成单位“1”,即100%,先求一个数是另一个数的百分之几,再根据所求问题把两个百分数相减。
在实际生活中,人们常用“增加百分之几”“减少百分之几”“节约百分之几”……来表示增加、减少的幅度。
你知道上面这些话的含义吗?举例说一说。
解答“谁比谁多百分之几”的问题的解题关键是什么?
弄懂问题是求哪部分数占单位“1”的百分之几,找准单位“1”。
课堂讨论:
说一说:
下列句子是求谁占谁的百分之几?哪个量是单位“1”?
①今年产量比去年多百分之几?
③彩电降价了百分之几?
②这个月用电比上个月节约了百分之几?
(和去年比较,去年产量是单位“1”)
(和上个月比较,上个月用电量是单位“1”)
(现价和原价比较,原价是单位“1”)
1、小飞家原来每月用水约10t,更换了节水龙头后
每月用水约9t,每月用水比原来节约了百分之几?
(10-9)÷10
=1÷10
=10%
答:每月用水比原来节约了10%。
求现在每月用水比原来节约了百分之几,就是求现在每月比原来每月少用的用水量是原来每月用水量的百分之几。原来每月的用水量是单位“1”。
①80千克比50千克多( )千克,
多( )%。
②50千克比80千克少( )千克,
少( )%。
③50千克是80千克的( )%。
④80千克是50千克的( )%。
2、填一填
30
60
30
37.5
62.5
160
①一个足球运动员,经训练速度提高了2%米。( )
②甲数比乙数多10%,乙数就比甲数少10%。 ( )
③王师傅生产了100个零件,结果98个零件合格,合格的零件占生产零件总数的98%。 ( )
×
×
√
3、判断。
4、姐姐身高150厘米,比弟弟高10厘米。求姐姐比弟弟
高百分之几的算式是( )。
①10÷150 ②10÷(150-10)
③(150-10)÷150 ④10÷(150+10)
正确答案选②。
不要认为降低百分之几,提高百分之几……一定要用一个数减去另一个数的差除以标准量,应仔细审题,如果解题时所需数量给出,就直接使用。
同学们,这节课你都学到了什么?
求一个数比另一个数多(或少)百分之几
求一个数比另一个数多(或少)百分之几,可以先求多(或少)的部分,再求多(或少)的部分是另一个数的百分之几;也可以先求一个数是另外一个数的百分之几,再求比另外一个数多(或少)百分之几。
人教版 六年级上册
第6单元 百分数(一)
第 5 课时 解决问题(2)
1、为了缓解交通拥挤的状况,某市正在进行道路拓宽。
团结路的路宽由原来的12m增加到25m,拓宽了百
分之几?
(25-12)÷12
=13÷12
≈ 108.3%
答:拓宽了108.3%。
求拓宽了百分之几,就是求现在的路宽比原来的路宽多出来的宽度是原来路宽的百分之几。原来的路宽是单位“1”。
2、六年级学生去植树,男生植树320棵,比女生多20%,比女生多植了多少棵?
例4:学校图书室原有图书1400册,今年图书册数增加了12%。现在图书室有多少册图书?
已知条件 原有图书1400册,今年图书册数增加了12%。
所求问题
现在图书室有多少册图书?
分析信息:
例4:学校图书室原有图书1400册,今年图书册数增加了12%。现在图书室有多少册图书?
把原来图书总册数看作单位“1”。
1400×12%=168(册)
1400+168=1568(册)
答:现在图书室有1568册图书。
1400×(1+12%)
=1400×112%
=1568(册)
方法一:先求出今年比去年增加的图书册数,再加上原有的册数就是今年的册数。
方法二: 先求出今年图书册数是原有图书册数的百分之几,再求出今年的册数。
探索新知
做一做:
龙泉镇去年有小学生2800人,今年比去年减少了
0.5%。今年有小学生多少人?
方法一:
2800-2800×0.5%
=2800-14
=2786(人)
答:今年有小学生2786人。
方法二:
2800×(1-0.5%)
=2800×99.5%
=2786(人)
答:今年有小学生2786人。
怎样求比一个数多(或少)百分之几的数是多少?
小结:
求比一个数多(或少)百分之几的数是多少与求比一个数多(或少)几分之几的思路相同;
方法一是先求多(或少)的数;
方法二是先求要求的数是这个数的百分之几。
小组讨论:
1、一个工厂由于采用了新工艺,现在每件产品成本是37.4元,比原来降低了15%。原来每件产品的成本是多少元?
单位“1”
现成本﹦原成本-降低的成本
(原成本×15%)
解:设原来每件成本x元。
x-15%x=37.4
算术方法解:
数量÷对应分率=单位“1”的量
单位“1”的量未知,可用方程解答。
37.4
(1-15%)
现成本
现成本占单位“1”的百分率
÷
巩固拓展
想一想,还可以怎样做?
2.袁隆平院士是我国著名科学家,被誉为“杂交水稻之父”。2021年,袁隆平院士指导的杂交水稻示范片双季稻年平均产量达到了每公顷24.06t,比攻关目标高了约7 % 。攻关目标约是每公顷多少吨 ( 得数保留一位小数。)
解:设2021年全国平均每公顷水稻产量大约是xt。
(1+7%)x=24.06
1.07x=24.06
x=24.06÷1.07
x≈22.49
答:2021年全国平均每公顷水稻产量大约是7.57吨。
同学们,这节课你都学到了什么?
百分数应用题的解题思路和分数应用题的相同。
1、单位“1”的量已知,根据求一个数的几分之几是多少用乘法计算。
2、单位“1”的量未知,可根据等量关系列方程或用除法计算。
关键是找准单位“1”。
数量÷对应分率=单位“1”的对应量
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
