北师大版九年级上册1.3 正方形的判定课件(共24张PPT)
文档属性
| 名称 | 北师大版九年级上册1.3 正方形的判定课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 597.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 16:08:04 | ||
图片预览





文档简介
(共24张PPT)
第一章 特殊平行四边形
1.2.2 正方形的判定
学习目标
1.探索并证明正方形的判定,并了解平行四边形、
矩形、菱形之间的联系和区别;(重点、难点)
2.会运用正方形的判定条件进行有关的论证和计算 .
(难点)
问题1 什么是正方形?正方形有哪些性质?
A
B
C
D
O
新课导入
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分;
④既是中心对称图形也是轴对称图形.
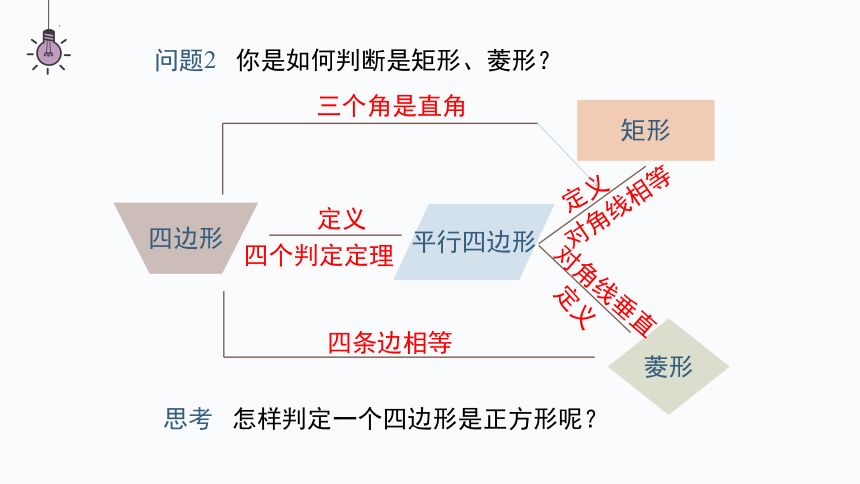
问题2 你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
思考 怎样判定一个四边形是正方形呢?
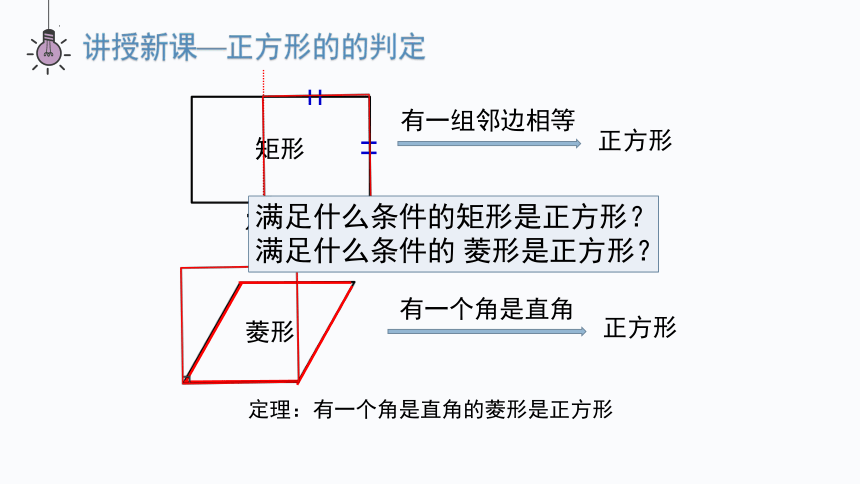
讲授新课—正方形的的判定
有一个角是直角
菱形
正方形
有一组邻边相等
正方形
矩形
定理:有一组邻边相等的矩形是正方形
定理:有一个角是直角的菱形是正方形
满足什么条件的矩形是正方形?满足什么条件的 菱形是正方形?
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线互相垂直的矩形是正方形.
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线相等的菱形是正方形.
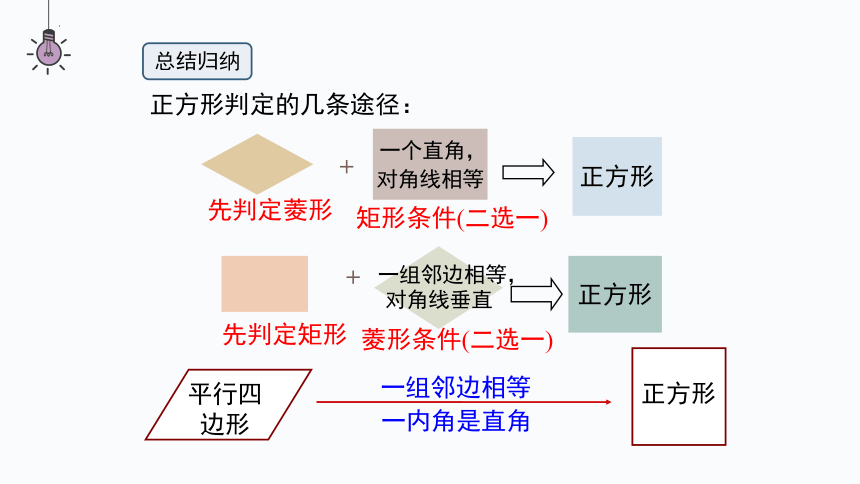
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角,
一组邻边相等,
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等
一内角是直角
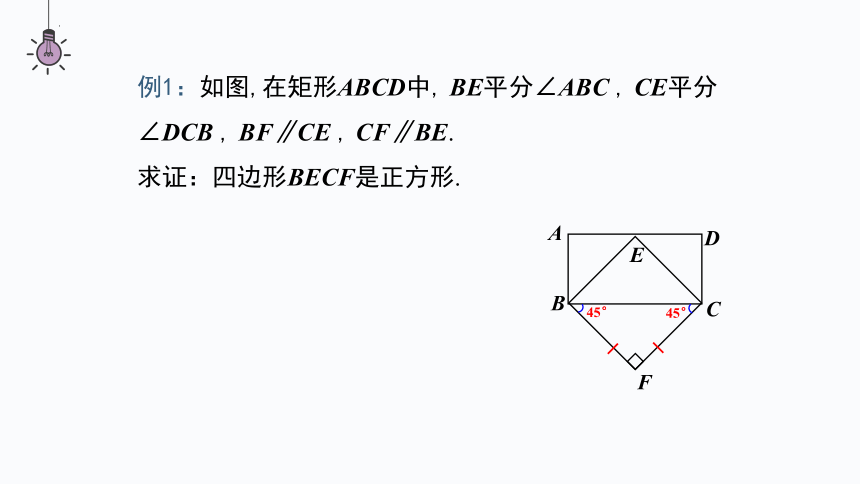
例1:如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.
F
A
B
E
C
D
45°
45°
F
A
B
E
C
D
证明: ∵ BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°,
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
练一练
C
A
B
C
D
O
讲授新课—奇妙的中点四边形
探索一:如图,在四边形ABCD中,E、F、G、H分别是AB、AD、BC、DC的中点,连接EF,GH。
(1)请猜想EF和GH的关系;
(2)连接EG、FH,则四边形EFHG是_________.
探索二:如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
平行四边形
矩形
菱形
正方形
探索二:如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
平行四边形的中点四边形是平行四边形
矩形的中点四边形是菱形
菱形的中点四边形是矩形
正方形的中点四边形是正方形
探索三:请你设计一个中点四边形为正方形,但原四边形不是正方形的四边形
想一想:原四边形的对角线有哪些特点?
相等且垂直
“筝形”
探索四:一般四边形的中点四边形
原四边形 对角线关系
所得中点 四边形
垂直不相等
菱形
相等不垂直
矩形
不相等
不垂直
平行四边形
相等且垂直
正方形
1.下列命题正确的是( )
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
D
随堂练习
2.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
D
3.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA
=90°,请添加一个条件____________________,可得出该四边形是正方形.
AB=BC(答案不唯一)
A
B
C
D
O
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________________(只填写序号).
②③或①④
5. 证明:有一个角是直角的菱形是正方形
教材P24随堂练习(1)
6.已知:如图,E,F 是正方形 ABCD 的对角线 BD 上的两点,且 BE = DF.
求证:四边形 AECF 是菱形
证明:∵四边形ABCD是正方形,
∴AD=CB,AD∥CB.
∴∠ADF=∠CBE.
又∵BE=DF,
∴△ADF≌△CBE(SAS),
∴AF=CE,∠AFD=∠CEB.
∴∠AFE=∠CEF.∴AF∥CE.
∴四边形AECF是平行四边形.
∵AD=AB,∴∠ADF=∠ABE.
又∵BE=DF,∴△AFD≌△AEB(SAS).
∴AF=AE.
∴四边形AECF是菱形(一组邻边相等的平行四边形是菱形).
教材P25知识技能2
7.如图,在正方形 ABCD 中,E,F,G,H 分别在它的四条边上,且 AE = BF = CG = DH.四边形 EFGH 是什么特殊四边形?你是如何判断的?
解:四边形EFGH是正方形.
理由如下:在正方形ABCD中,
AB=BC=CD=AD,
∠A=∠B=∠C=∠D=90°.
∵AE=BF=CG=DH,
∴BE=CF=DG=AH.
∴△AEH≌△BFE≌△CGF≌△DHG(SAS).
∴∠AEH=∠DHG,HE=EF=FG=GH.
∴四边形EFGH是菱形.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
教材P25数学理解3
8.如图,正方形ABCD 的对角线相交于点 O,正方形 A' B' C' O 与正方形 ABCD 的边长相等.在正方形 A' B' C' O 绕点 O 旋转的过程中,两个正方形重叠部分的面积与正方形 ABCD 的面积有什么关系?请证明你的结论
解:重叠部分的面积等于正方形ABCD面积的 .证明如下:
①重叠部分为等腰直角三角形时,重叠部分的面积为正方形ABCD面积的 ,即S重叠=S△AOB=S△BOC=
S△COD=S△AOD= S正方形ABCD.
②重叠部分为四边形时,设OA′与AB相交于
点E,OC′与BC相交于点F.
∵四边形ABCD是正方形,
∴OA=OB,∠EAO=∠FBO=45°,∠AOB=90°
又∵∠A'OC'=90°,∴∠AOE=∠BOF.
∴△AOE≌△BOF(AAS).
∴S△AOE=S△BOF.
∴S重叠=S△BOE+S△BOF=S△BOE+S△AOE=
S△AOB= S正方形ABCD.
综上,重叠部分的面积等于正方形ABCD面积的 .
教材P25联系拓广
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
课堂小结
第一章 特殊平行四边形
1.2.2 正方形的判定
学习目标
1.探索并证明正方形的判定,并了解平行四边形、
矩形、菱形之间的联系和区别;(重点、难点)
2.会运用正方形的判定条件进行有关的论证和计算 .
(难点)
问题1 什么是正方形?正方形有哪些性质?
A
B
C
D
O
新课导入
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分;
④既是中心对称图形也是轴对称图形.
问题2 你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
思考 怎样判定一个四边形是正方形呢?
讲授新课—正方形的的判定
有一个角是直角
菱形
正方形
有一组邻边相等
正方形
矩形
定理:有一组邻边相等的矩形是正方形
定理:有一个角是直角的菱形是正方形
满足什么条件的矩形是正方形?满足什么条件的 菱形是正方形?
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线互相垂直的矩形是正方形.
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线相等的菱形是正方形.
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角,
一组邻边相等,
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等
一内角是直角
例1:如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.
F
A
B
E
C
D
45°
45°
F
A
B
E
C
D
证明: ∵ BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°,
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.
在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
练一练
C
A
B
C
D
O
讲授新课—奇妙的中点四边形
探索一:如图,在四边形ABCD中,E、F、G、H分别是AB、AD、BC、DC的中点,连接EF,GH。
(1)请猜想EF和GH的关系;
(2)连接EG、FH,则四边形EFHG是_________.
探索二:如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
平行四边形
矩形
菱形
正方形
探索二:如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
平行四边形的中点四边形是平行四边形
矩形的中点四边形是菱形
菱形的中点四边形是矩形
正方形的中点四边形是正方形
探索三:请你设计一个中点四边形为正方形,但原四边形不是正方形的四边形
想一想:原四边形的对角线有哪些特点?
相等且垂直
“筝形”
探索四:一般四边形的中点四边形
原四边形 对角线关系
所得中点 四边形
垂直不相等
菱形
相等不垂直
矩形
不相等
不垂直
平行四边形
相等且垂直
正方形
1.下列命题正确的是( )
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
D
随堂练习
2.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
D
3.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA
=90°,请添加一个条件____________________,可得出该四边形是正方形.
AB=BC(答案不唯一)
A
B
C
D
O
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________________(只填写序号).
②③或①④
5. 证明:有一个角是直角的菱形是正方形
教材P24随堂练习(1)
6.已知:如图,E,F 是正方形 ABCD 的对角线 BD 上的两点,且 BE = DF.
求证:四边形 AECF 是菱形
证明:∵四边形ABCD是正方形,
∴AD=CB,AD∥CB.
∴∠ADF=∠CBE.
又∵BE=DF,
∴△ADF≌△CBE(SAS),
∴AF=CE,∠AFD=∠CEB.
∴∠AFE=∠CEF.∴AF∥CE.
∴四边形AECF是平行四边形.
∵AD=AB,∴∠ADF=∠ABE.
又∵BE=DF,∴△AFD≌△AEB(SAS).
∴AF=AE.
∴四边形AECF是菱形(一组邻边相等的平行四边形是菱形).
教材P25知识技能2
7.如图,在正方形 ABCD 中,E,F,G,H 分别在它的四条边上,且 AE = BF = CG = DH.四边形 EFGH 是什么特殊四边形?你是如何判断的?
解:四边形EFGH是正方形.
理由如下:在正方形ABCD中,
AB=BC=CD=AD,
∠A=∠B=∠C=∠D=90°.
∵AE=BF=CG=DH,
∴BE=CF=DG=AH.
∴△AEH≌△BFE≌△CGF≌△DHG(SAS).
∴∠AEH=∠DHG,HE=EF=FG=GH.
∴四边形EFGH是菱形.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
教材P25数学理解3
8.如图,正方形ABCD 的对角线相交于点 O,正方形 A' B' C' O 与正方形 ABCD 的边长相等.在正方形 A' B' C' O 绕点 O 旋转的过程中,两个正方形重叠部分的面积与正方形 ABCD 的面积有什么关系?请证明你的结论
解:重叠部分的面积等于正方形ABCD面积的 .证明如下:
①重叠部分为等腰直角三角形时,重叠部分的面积为正方形ABCD面积的 ,即S重叠=S△AOB=S△BOC=
S△COD=S△AOD= S正方形ABCD.
②重叠部分为四边形时,设OA′与AB相交于
点E,OC′与BC相交于点F.
∵四边形ABCD是正方形,
∴OA=OB,∠EAO=∠FBO=45°,∠AOB=90°
又∵∠A'OC'=90°,∴∠AOE=∠BOF.
∴△AOE≌△BOF(AAS).
∴S△AOE=S△BOF.
∴S重叠=S△BOE+S△BOF=S△BOE+S△AOE=
S△AOB= S正方形ABCD.
综上,重叠部分的面积等于正方形ABCD面积的 .
教材P25联系拓广
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
