人教版八年级上册11.2.2 三角形的外角 课件(共17张PPT)
文档属性
| 名称 | 人教版八年级上册11.2.2 三角形的外角 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 16:13:07 | ||
图片预览



文档简介
(共17张PPT)
11.2.2 三角形的外角
学习目标
1、了解三角形的外角
2、探索并了解三角形的一个外角等于它不相邻的两个内角的和;
3、学会运用简单的说理来计算三角形相关的角
重点和难点
重点:三角形的外角性质
难点:运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法。
2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
知识回顾
65°
60°
三角形的内角和等于180度
A
B
C
D
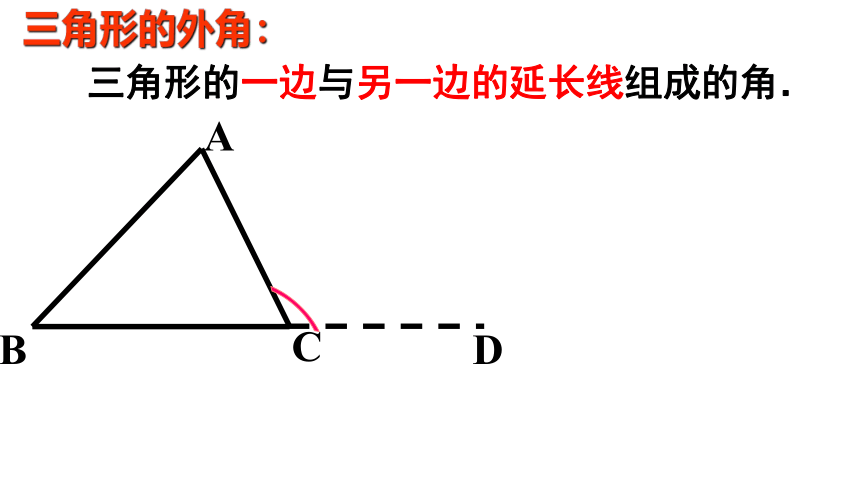
三角形的外角:
三角形的一边与另一边的延长线组成的角.
A
B
C
D
E
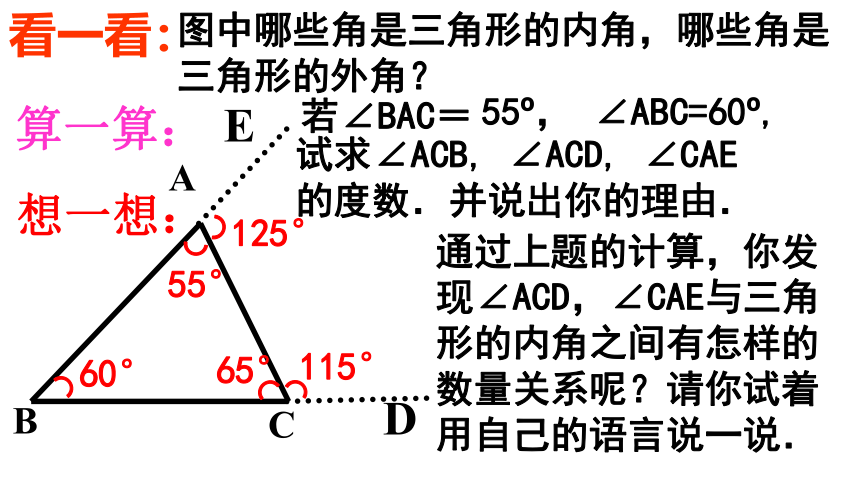
看一看:
算一算:
若∠BAC=
55 , ∠ABC=60 ,
试求∠ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
想一想:
通过上题的计算,你发现∠ACD,∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
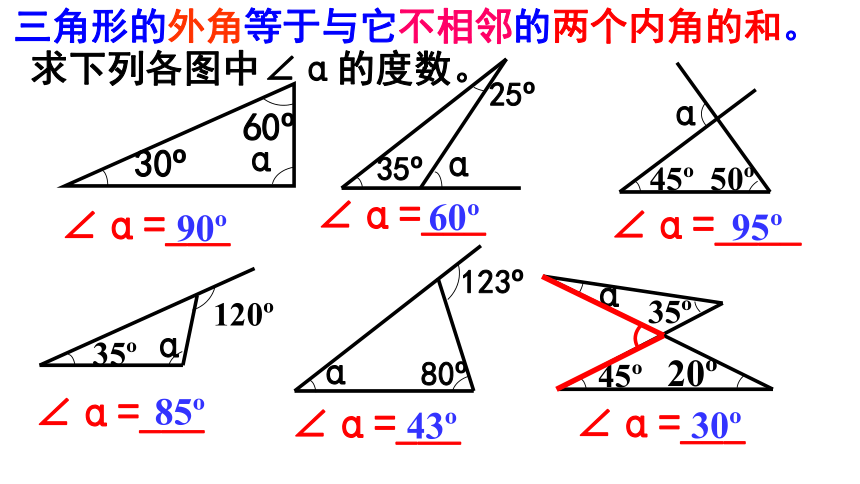
∠α=___
∠α=___
∠α=____
α
45
20
35
∠α=___
α
123
80
∠α=___
α
25
35
∠α=___
90
85
95
60
43
30
求下列各图中∠α的度数。
α
60
30
α
120
35
α
45
50
三角形的外角等于与它不相邻的两个内角的和。
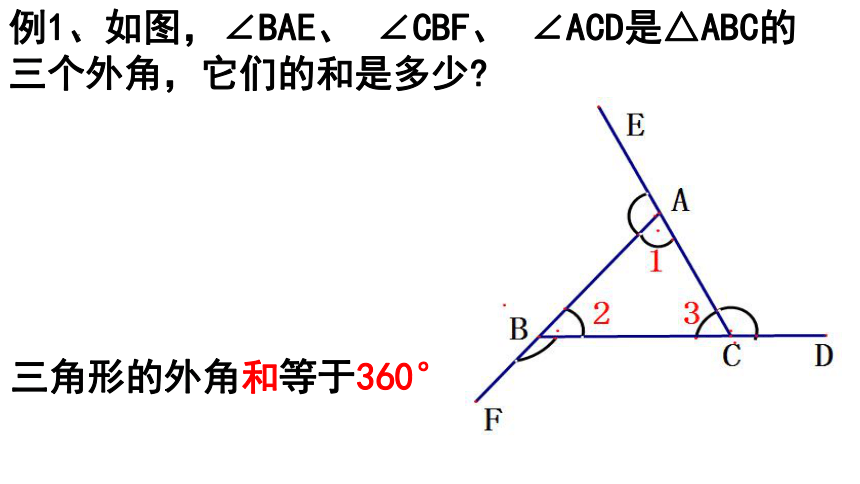
三角形的外角和等于360°
例1、如图,∠BAE、 ∠CBF、 ∠ACD是△ABC的三个外角,它们的和是多少
1、有一次小明看见这样一个图,要计算:∠A+∠B+∠C+∠D+∠E+∠F= 度
B
C
D
A
G
M
H
E
F
360
A
B
C
D
E
2、求∠A+∠B+∠C+∠D+∠E的度数
⌒
F
G
⌒
∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
例2:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
40
40
⌒
练一练
1、已知图中∠A、∠B、∠C分别为80°, 20°,30°,求∠1的度数
B
2
1
A
C
D
E
2、如图,试计算∠BOC的度数.
90
30
20
A
B
C
O
D
⌒
110°
3、如图,在Rt△ABC中,CD是斜边AB上的高,∠BCD=35°,求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
4.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,求∠A的度数.
A
E
G
F
C
B
45°
⌒
30°
⌒
70°
⌒
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
拓展与思考1
下面的推理题连名侦探柯南也被难住了.他希望同学们能尽快的帮他解决下面的问题.
根据下列线索推理出这个三角形有关的角。
线索1:在△ABC中,∠B=∠C ;
线索2:它的一个外角是100 ;
问题:它的各个内角各是多少度?
100°
B
C
A
100°
A
B
C
50°,50°,80°
或80°,80°,20°
答:它的各个内角分别为
拓展与思考2
2、三角形的外角的性质
1、三角形的内角和180°
三角形内角和外角的性质
三角形的外角等于与它不相邻的两个内角的和。
3、三角形的外角和等于3600。
小结
11.2.2 三角形的外角
学习目标
1、了解三角形的外角
2、探索并了解三角形的一个外角等于它不相邻的两个内角的和;
3、学会运用简单的说理来计算三角形相关的角
重点和难点
重点:三角形的外角性质
难点:运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法。
2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
知识回顾
65°
60°
三角形的内角和等于180度
A
B
C
D
三角形的外角:
三角形的一边与另一边的延长线组成的角.
A
B
C
D
E
看一看:
算一算:
若∠BAC=
55 , ∠ABC=60 ,
试求∠ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
想一想:
通过上题的计算,你发现∠ACD,∠CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
∠α=___
∠α=___
∠α=____
α
45
20
35
∠α=___
α
123
80
∠α=___
α
25
35
∠α=___
90
85
95
60
43
30
求下列各图中∠α的度数。
α
60
30
α
120
35
α
45
50
三角形的外角等于与它不相邻的两个内角的和。
三角形的外角和等于360°
例1、如图,∠BAE、 ∠CBF、 ∠ACD是△ABC的三个外角,它们的和是多少
1、有一次小明看见这样一个图,要计算:∠A+∠B+∠C+∠D+∠E+∠F= 度
B
C
D
A
G
M
H
E
F
360
A
B
C
D
E
2、求∠A+∠B+∠C+∠D+∠E的度数
⌒
F
G
⌒
∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
例2:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
40
40
⌒
练一练
1、已知图中∠A、∠B、∠C分别为80°, 20°,30°,求∠1的度数
B
2
1
A
C
D
E
2、如图,试计算∠BOC的度数.
90
30
20
A
B
C
O
D
⌒
110°
3、如图,在Rt△ABC中,CD是斜边AB上的高,∠BCD=35°,求∠A与∠EBC的度数.
A
B
C
D
E
∟
⌒
35°
⌒
⌒
4.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,求∠A的度数.
A
E
G
F
C
B
45°
⌒
30°
⌒
70°
⌒
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )
拓展与思考1
下面的推理题连名侦探柯南也被难住了.他希望同学们能尽快的帮他解决下面的问题.
根据下列线索推理出这个三角形有关的角。
线索1:在△ABC中,∠B=∠C ;
线索2:它的一个外角是100 ;
问题:它的各个内角各是多少度?
100°
B
C
A
100°
A
B
C
50°,50°,80°
或80°,80°,20°
答:它的各个内角分别为
拓展与思考2
2、三角形的外角的性质
1、三角形的内角和180°
三角形内角和外角的性质
三角形的外角等于与它不相邻的两个内角的和。
3、三角形的外角和等于3600。
小结
