人教版八年级上册11.3.2 多边形的内角和课件(共14张PPT)
文档属性
| 名称 | 人教版八年级上册11.3.2 多边形的内角和课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 96.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
11.3.2 多边形内角和
(1)掌握多边形的内角和的计算方法,并能用内角和知识解决一些较简单的问题;
(2)通过多边形内角和的计算公式的推导,培养探索和归纳的能力;
(3) 体验转化的数学思想方法。
学习目标
重点与难点:
(1)重点:多边形内角和以及外角和;
(2)难点:多边形内角和以及外角和的推导。
2、在多边形中连接________________________的线段叫做多边形的对角线。
1、在平面内, ____________________________叫做多边形。
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点
知识回顾
3、一个 n 边形从一个顶点可以引____条对角线,把 n 边形分成________个三角形.一个 n 边形一共有_______ 条对角线.
4、三角形内角和为_____,长方形和正方形内角和为______.
(n-2)
(n-3)
180°
360°
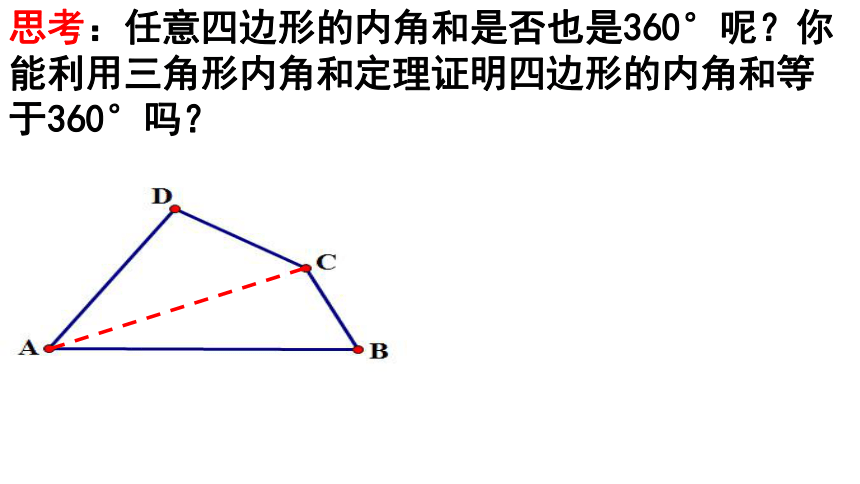
思考:任意四边形的内角和是否也是360°呢?你能利用三角形内角和定理证明四边形的内角和等于360°吗?
B
C
D
A
A
B
D
C
A
B
C
D
E
B
C
D
A
E
E
E
①
⑤
④
③
②
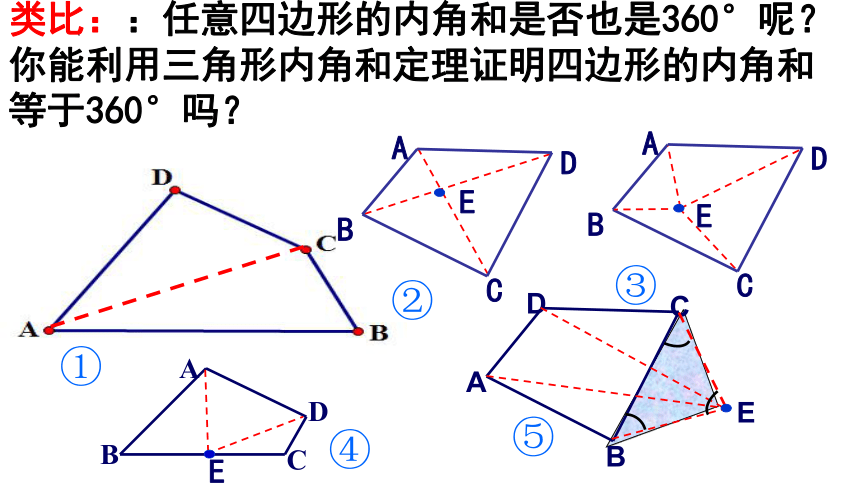
类比::任意四边形的内角和是否也是360°呢?你能利用三角形内角和定理证明四边形的内角和等于360°吗?
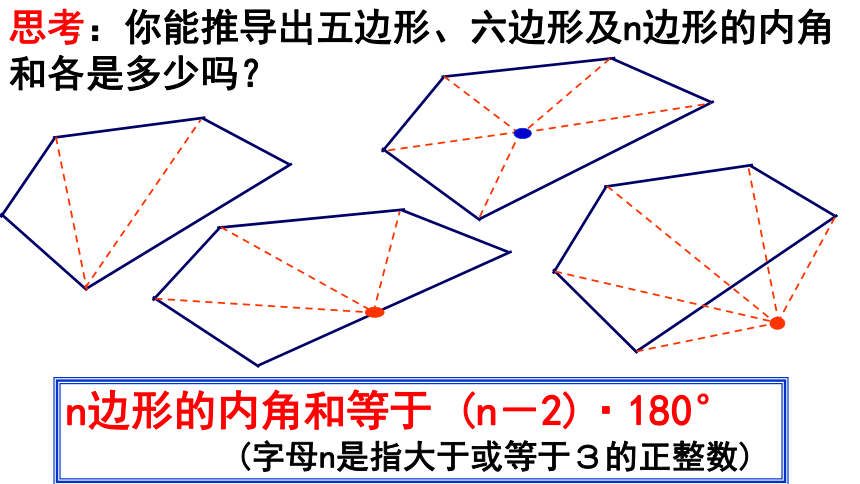
思考:你能推导出五边形、六边形及n边形的内角和各是多少吗?
n边形的内角和等于 (n-2)·180°
(字母n是指大于或等于3的正整数)
n边形的内角和等于 (n-2)·180°
(字母n是指大于或等于3的正整数)
练习:
1、八边形的内角和是 ___,十边形的内角和是___。
2、一个多边形的内角和是1800°,它是 ___边形。
3、求下列图形中x的值:
(3)
∟
(1)
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
C
B
D
分析:如图,已知四边形ABCD中
∠A+∠C=180°,试判断∠B与
∠D有何关系
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
思考:如果将六边形换为n边形(是不小于3的任意整数),可以得到同样的结果吗?
n边形的外角和等于360°
练习:1.一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
2.一个多边形的内角和等于外角和的2倍,求这个多边形的边数。
n边形的内角和等于 (n-2)·180°
(字母n是指大于或等于3的正整数)
n边形的外角和等于360°
今天的收获
1、n 边形的内角和等于(n-2)×180°.
3、利用类比归纳、转化的学习方法,可以把多边形问题转化为三角形问题来解决; 外角问题转化为内角来解决.
4、方程的数学思想在几何中有重要的作用.
本节课你学会哪些知识?学会了哪些解决问题的方法?你还有哪些疑问?
2、n 边形的外角和等于360°.
检测:
1、(1)一个多边形的各内角都等于120°,则这是一个_____边形
(2)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(3)一个多边形的内角和等于它的外角和,那么这个多边形是____边形.
(4)如果一个多边形的边数增加一条,那么这个多边形的内角和增加______,外角和增加_____.
2.某校为发展学生的兴趣和爱好,划出一块三角形和四边形区域作生物园,计划在两个生物园的各个角落种植半径为R的扇形区域鲜花,请算一算每一个生物园中的扇形区域鲜花占地面积.
11.3.2 多边形内角和
(1)掌握多边形的内角和的计算方法,并能用内角和知识解决一些较简单的问题;
(2)通过多边形内角和的计算公式的推导,培养探索和归纳的能力;
(3) 体验转化的数学思想方法。
学习目标
重点与难点:
(1)重点:多边形内角和以及外角和;
(2)难点:多边形内角和以及外角和的推导。
2、在多边形中连接________________________的线段叫做多边形的对角线。
1、在平面内, ____________________________叫做多边形。
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点
知识回顾
3、一个 n 边形从一个顶点可以引____条对角线,把 n 边形分成________个三角形.一个 n 边形一共有_______ 条对角线.
4、三角形内角和为_____,长方形和正方形内角和为______.
(n-2)
(n-3)
180°
360°
思考:任意四边形的内角和是否也是360°呢?你能利用三角形内角和定理证明四边形的内角和等于360°吗?
B
C
D
A
A
B
D
C
A
B
C
D
E
B
C
D
A
E
E
E
①
⑤
④
③
②
类比::任意四边形的内角和是否也是360°呢?你能利用三角形内角和定理证明四边形的内角和等于360°吗?
思考:你能推导出五边形、六边形及n边形的内角和各是多少吗?
n边形的内角和等于 (n-2)·180°
(字母n是指大于或等于3的正整数)
n边形的内角和等于 (n-2)·180°
(字母n是指大于或等于3的正整数)
练习:
1、八边形的内角和是 ___,十边形的内角和是___。
2、一个多边形的内角和是1800°,它是 ___边形。
3、求下列图形中x的值:
(3)
∟
(1)
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
C
B
D
分析:如图,已知四边形ABCD中
∠A+∠C=180°,试判断∠B与
∠D有何关系
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
思考:如果将六边形换为n边形(是不小于3的任意整数),可以得到同样的结果吗?
n边形的外角和等于360°
练习:1.一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
2.一个多边形的内角和等于外角和的2倍,求这个多边形的边数。
n边形的内角和等于 (n-2)·180°
(字母n是指大于或等于3的正整数)
n边形的外角和等于360°
今天的收获
1、n 边形的内角和等于(n-2)×180°.
3、利用类比归纳、转化的学习方法,可以把多边形问题转化为三角形问题来解决; 外角问题转化为内角来解决.
4、方程的数学思想在几何中有重要的作用.
本节课你学会哪些知识?学会了哪些解决问题的方法?你还有哪些疑问?
2、n 边形的外角和等于360°.
检测:
1、(1)一个多边形的各内角都等于120°,则这是一个_____边形
(2)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(3)一个多边形的内角和等于它的外角和,那么这个多边形是____边形.
(4)如果一个多边形的边数增加一条,那么这个多边形的内角和增加______,外角和增加_____.
2.某校为发展学生的兴趣和爱好,划出一块三角形和四边形区域作生物园,计划在两个生物园的各个角落种植半径为R的扇形区域鲜花,请算一算每一个生物园中的扇形区域鲜花占地面积.
