人教版八年级上册12.2三角形全等的判定(HL) 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级上册12.2三角形全等的判定(HL) 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 297.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
八年级 上册
12.2 三角形全等的判定
(H L)
学习目标:
探索并掌握两个直角三角形全等的“HL”
判定方法;
会用直角三角形判定方法解决一些较简单实
际问题.
学习重点:
直角三角形全等的判定定理的理解和应用;
学习难点:
已知斜边和一条直角边,作直角三角形;
利用直角三角形全等的判定定理解决问题
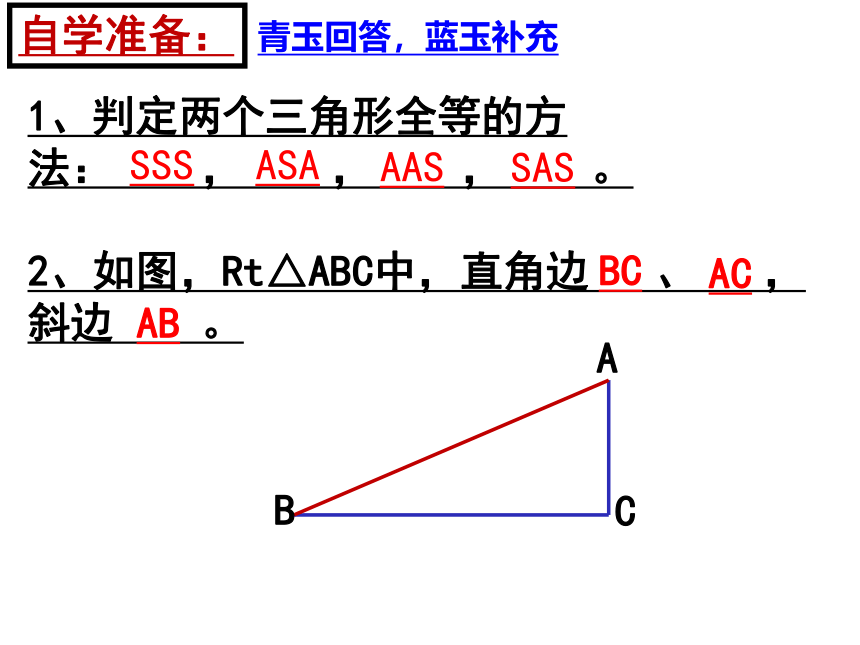
1、判定两个三角形全等的方法: , , , 。
SSS
ASA
AAS
SAS
2、如图,Rt△ABC中,直角边 、 ,斜边 。
A
B
C
BC
AC
AB
自学准备:
青玉回答,蓝玉补充
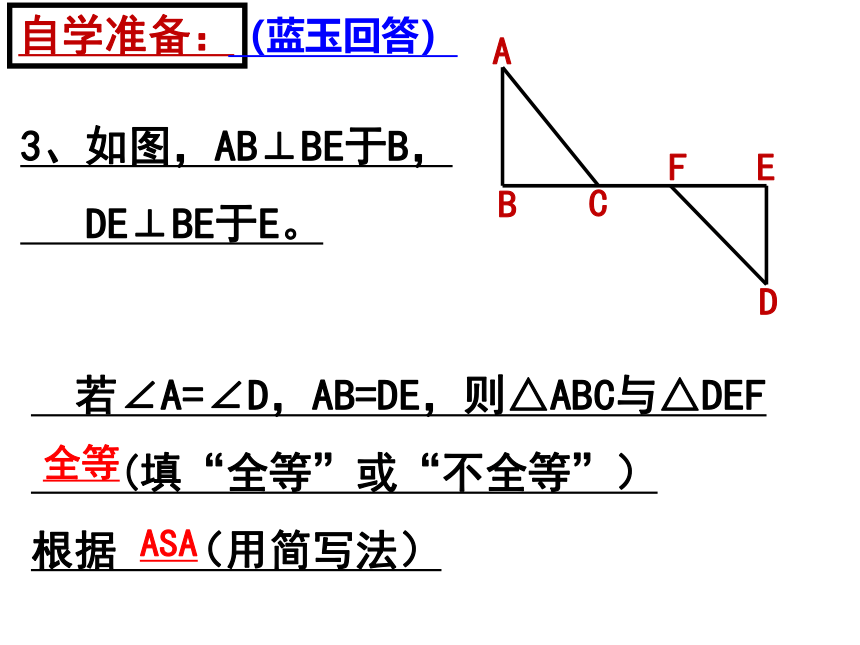
A
B
C
D
E
F
3、如图,AB⊥BE于B,
DE⊥BE于E。
若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”)
根据 (用简写法)
全等
ASA
自学准备:
(蓝玉回答)
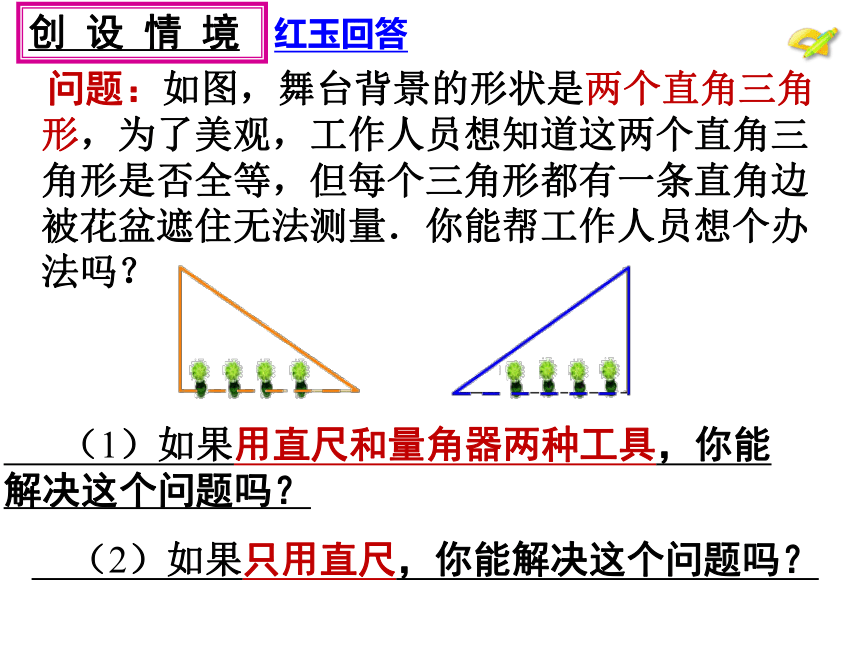
问题:如图,舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
创 设 情 境
(1)如果用直尺和量角器两种工具,你能解决这个问题吗?
红玉回答
(2)如果只用直尺,你能解决这个问题吗?
A
B
C
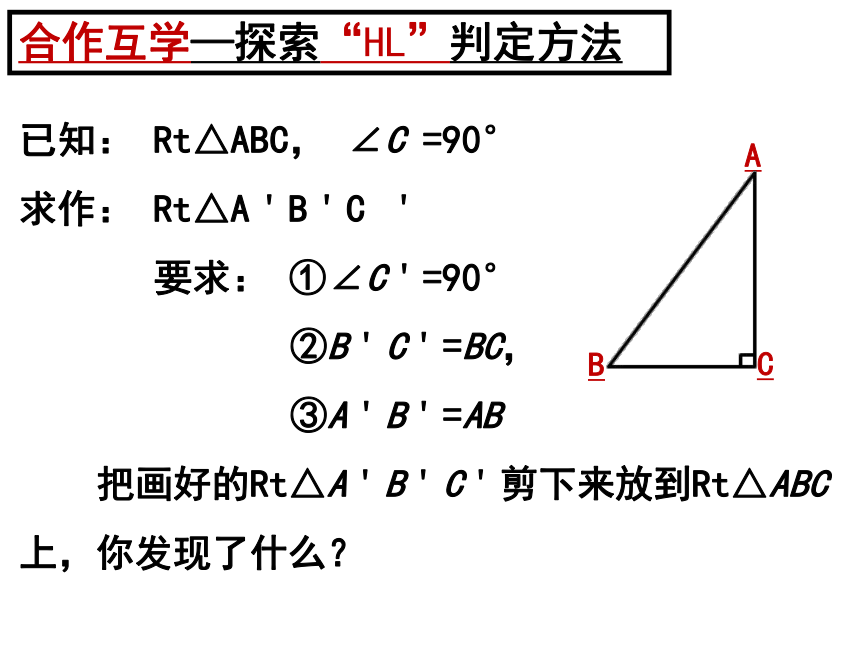
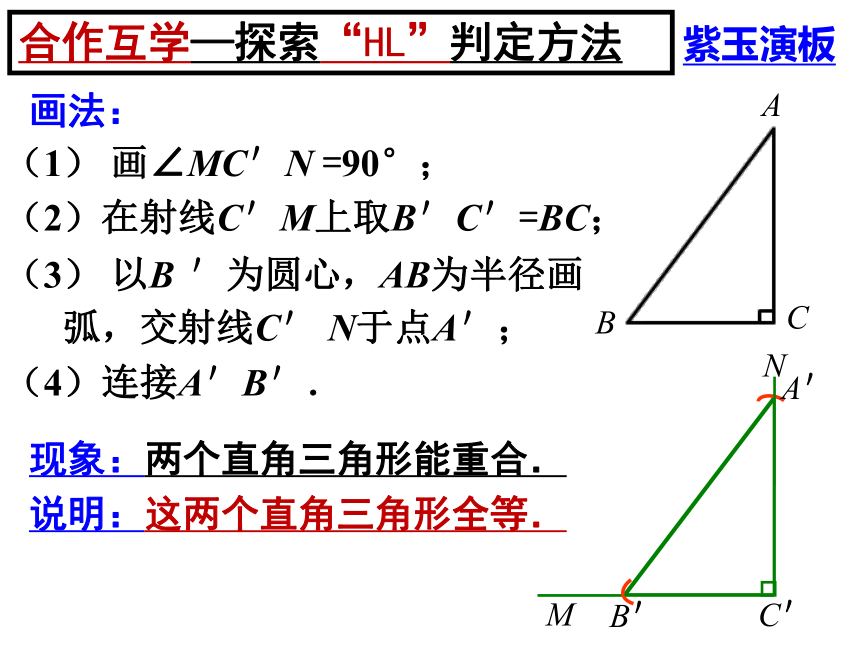
合作互学—探索“HL”判定方法
已知: Rt△ABC, ∠C =90°
求作: Rt△A'B'C '
要求: ①∠C'=90°
②B'C'=BC,
③A'B'=AB
把画好的Rt△A'B'C'剪下来放到Rt△ABC上,你发现了什么?
A
B
C
(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B '为圆心,AB为半径画
弧,交射线C' N于点A';
(4)连接A'B'.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A'
N
M
C'
B'
合作互学—探索“HL”判定方法
紫玉演板
判定两个直角三角形全等的一个定理:
斜边和一条直角边分别相等的两个直角三角形全等(简写为“斜边、直角边”或“HL”).
A
B
C
A'
B'
C'
几何语言:
在Rt△ABC 和 Rt△A'B'C'中,
AB =A'B',
BC =B'C',
∴ Rt△ABC Rt△A 'B 'C '(HL)
合作互学—探索“HL”判定方法
(红玉回答)
≌
精讲导学1—直角三角形的判定方法
如图,下面哪个选项可以直接用“HL”判定Rt△ABC 和 Rt△DEF全等( )
A、AC=DF,BC=EF
B、∠A =∠D,AB=DE
C、AC=DF,AB=DE
D、∠B =∠E,BC=EF
A
B
C
D
F
E
C
(SAS)
(AAS)
(HL)
(ASA)
你能用几种方法判定两个直角三角形全等?
直角三角形是特殊的三角形。
①定义 ⑥HL
②SAS
③ASA
④AAS
⑤SSS
精讲导学1—直角三角形的判定方法:
一般三角形判定
全等的方法:
①定义
②SAS
③ASA
④AAS
⑤SSS
(蓝玉回答,红玉补充或评价)
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D=90 °
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
例1 :如图,AC⊥BC,BD⊥AD,AC =BD.
求证:BC =AD.
A
B
C
D
精讲导学2—“HL”判定方法的运用
变式:如图 AC⊥BC,BD⊥AD,要证△ABC ≌△BAD,需要添加一个什么条件?
请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
A
B
C
D
精讲导学2—直角三角形判定方法的运用
例2:如图,在△ABC 中,
D是BC边的中点,
DE⊥AB于点E,
DF⊥AC于点F,
BE =CF.
精讲导学3—直角三角形判定方法的运用
(1)图中有几对全等三角形?请列举;
(2)选择一对你认为全等的三角形说明理由。
练习:如图AB =CD,AE⊥BC,DF⊥BC,垂足分别为E 、F,CE =BF.求证:AE=DF.
A
B
C
D
E
F
展示竞学—直角三角形判定方法的运用
(1)“HL”判定三角形全等应满足什么条件?
(2)判定两个直角三角形全等有哪些方法?
(3)把这节课学习的感悟与大家分享一下吧!
课堂小结
A
B
C
D
F
E
检测固学—直角三角形判定方法的运用
如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E、F,BF=DE。
求证:AB//CD
八年级 上册
12.2 三角形全等的判定
(H L)
学习目标:
探索并掌握两个直角三角形全等的“HL”
判定方法;
会用直角三角形判定方法解决一些较简单实
际问题.
学习重点:
直角三角形全等的判定定理的理解和应用;
学习难点:
已知斜边和一条直角边,作直角三角形;
利用直角三角形全等的判定定理解决问题
1、判定两个三角形全等的方法: , , , 。
SSS
ASA
AAS
SAS
2、如图,Rt△ABC中,直角边 、 ,斜边 。
A
B
C
BC
AC
AB
自学准备:
青玉回答,蓝玉补充
A
B
C
D
E
F
3、如图,AB⊥BE于B,
DE⊥BE于E。
若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”)
根据 (用简写法)
全等
ASA
自学准备:
(蓝玉回答)
问题:如图,舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
创 设 情 境
(1)如果用直尺和量角器两种工具,你能解决这个问题吗?
红玉回答
(2)如果只用直尺,你能解决这个问题吗?
A
B
C
合作互学—探索“HL”判定方法
已知: Rt△ABC, ∠C =90°
求作: Rt△A'B'C '
要求: ①∠C'=90°
②B'C'=BC,
③A'B'=AB
把画好的Rt△A'B'C'剪下来放到Rt△ABC上,你发现了什么?
A
B
C
(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B '为圆心,AB为半径画
弧,交射线C' N于点A';
(4)连接A'B'.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A'
N
M
C'
B'
合作互学—探索“HL”判定方法
紫玉演板
判定两个直角三角形全等的一个定理:
斜边和一条直角边分别相等的两个直角三角形全等(简写为“斜边、直角边”或“HL”).
A
B
C
A'
B'
C'
几何语言:
在Rt△ABC 和 Rt△A'B'C'中,
AB =A'B',
BC =B'C',
∴ Rt△ABC Rt△A 'B 'C '(HL)
合作互学—探索“HL”判定方法
(红玉回答)
≌
精讲导学1—直角三角形的判定方法
如图,下面哪个选项可以直接用“HL”判定Rt△ABC 和 Rt△DEF全等( )
A、AC=DF,BC=EF
B、∠A =∠D,AB=DE
C、AC=DF,AB=DE
D、∠B =∠E,BC=EF
A
B
C
D
F
E
C
(SAS)
(AAS)
(HL)
(ASA)
你能用几种方法判定两个直角三角形全等?
直角三角形是特殊的三角形。
①定义 ⑥HL
②SAS
③ASA
④AAS
⑤SSS
精讲导学1—直角三角形的判定方法:
一般三角形判定
全等的方法:
①定义
②SAS
③ASA
④AAS
⑤SSS
(蓝玉回答,红玉补充或评价)
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D=90 °
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
例1 :如图,AC⊥BC,BD⊥AD,AC =BD.
求证:BC =AD.
A
B
C
D
精讲导学2—“HL”判定方法的运用
变式:如图 AC⊥BC,BD⊥AD,要证△ABC ≌△BAD,需要添加一个什么条件?
请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
A
B
C
D
精讲导学2—直角三角形判定方法的运用
例2:如图,在△ABC 中,
D是BC边的中点,
DE⊥AB于点E,
DF⊥AC于点F,
BE =CF.
精讲导学3—直角三角形判定方法的运用
(1)图中有几对全等三角形?请列举;
(2)选择一对你认为全等的三角形说明理由。
练习:如图AB =CD,AE⊥BC,DF⊥BC,垂足分别为E 、F,CE =BF.求证:AE=DF.
A
B
C
D
E
F
展示竞学—直角三角形判定方法的运用
(1)“HL”判定三角形全等应满足什么条件?
(2)判定两个直角三角形全等有哪些方法?
(3)把这节课学习的感悟与大家分享一下吧!
课堂小结
A
B
C
D
F
E
检测固学—直角三角形判定方法的运用
如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E、F,BF=DE。
求证:AB//CD
