有理数的乘法(一)[上学期]
文档属性
| 名称 | 有理数的乘法(一)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 141.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-20 17:49:00 | ||
图片预览




文档简介
课件21张PPT。有理数乘法渔亭中学 程棋德水库水位的变化
甲水库第一天
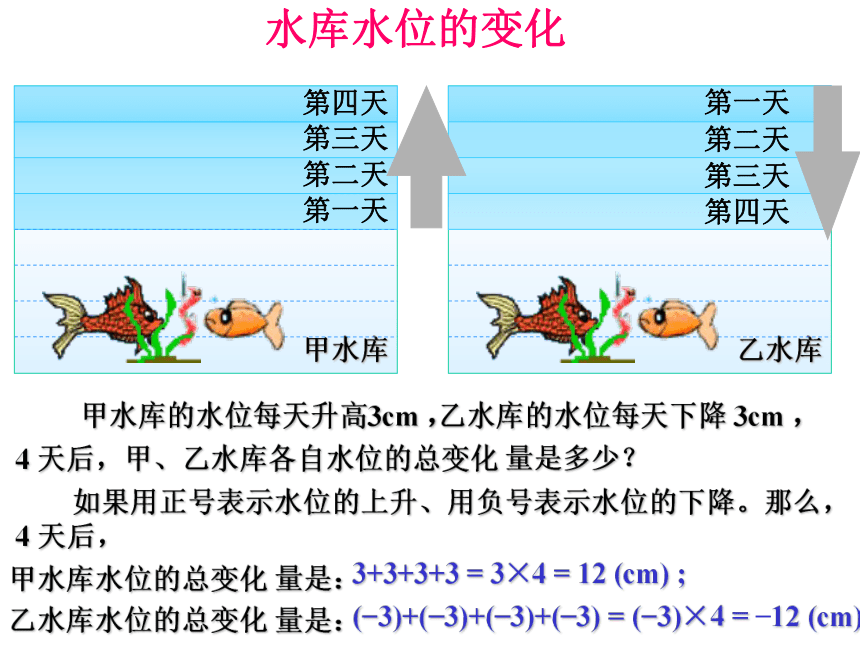
乙水库甲水库的水位每天升高3cm ,第二天第三天第四天乙水库的水位每天下降 3cm , 第一天 第二天 第三天 第四天4 天后,甲、乙水库各自水位的总变化 量是多少? 如果用正号表示水位的上升、用负号表示水位的下降。那么,4 天后,甲水库水位的总变化 量是:
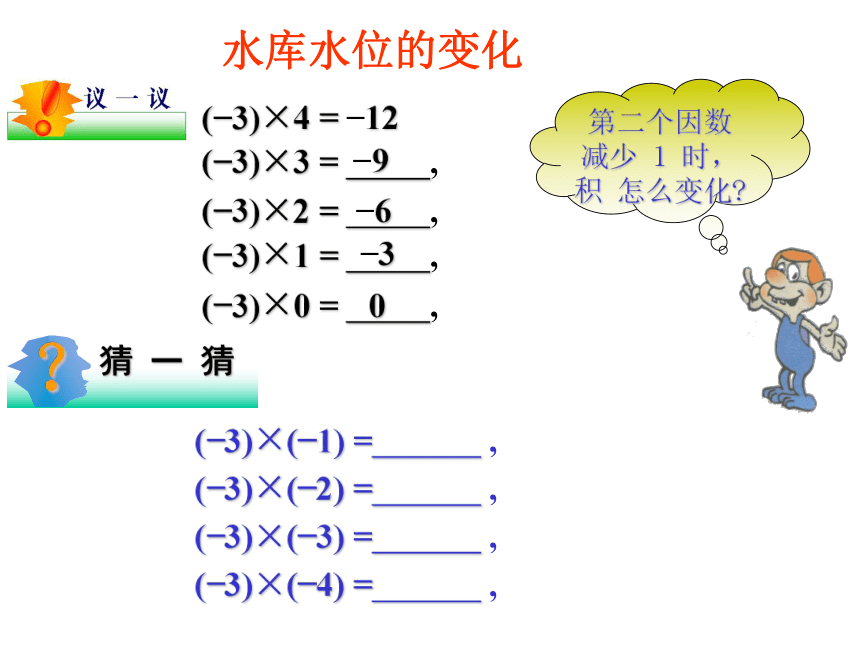
乙水库水位的总变化 量是:3+3+3+3 = 3×4 = 12 (cm) ;(?3)+(?3)+(?3)+(?3) = (?3)×4 = ?12 (cm) ;水库水位的变化(?3)×4 = ?12(?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,第二个因数减少 1 时,积 怎么变化?引例1 蜗牛运动 设蜗牛现在的位置为点O,若它一直都是沿直线爬行,而且每分钟爬行2cm,问:
(1)向右爬行,3分钟后的位置?
(2)向左爬行,3分钟后的位置?
(3)向右爬行,3分钟前的位置?
(4)向左爬行,3分钟前的位置?
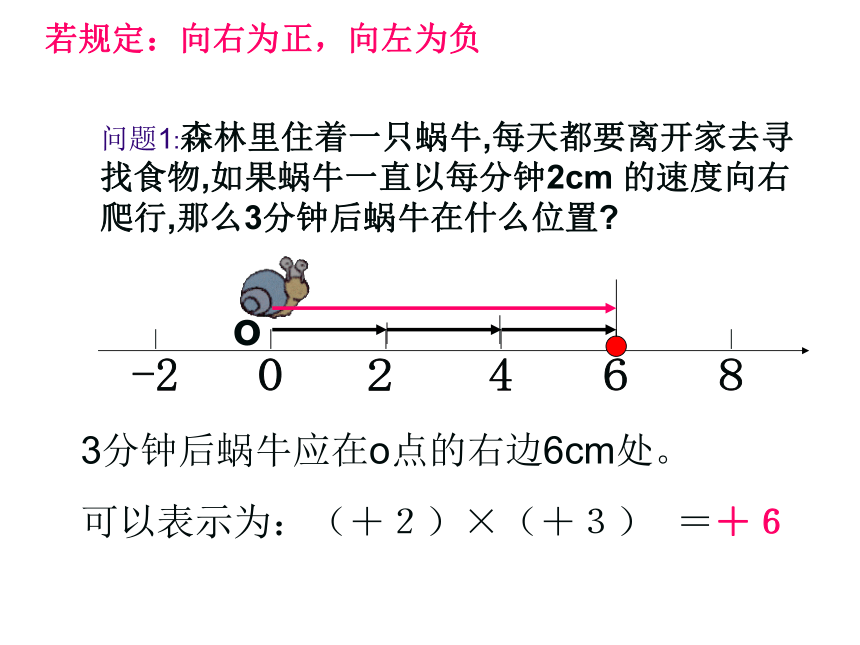
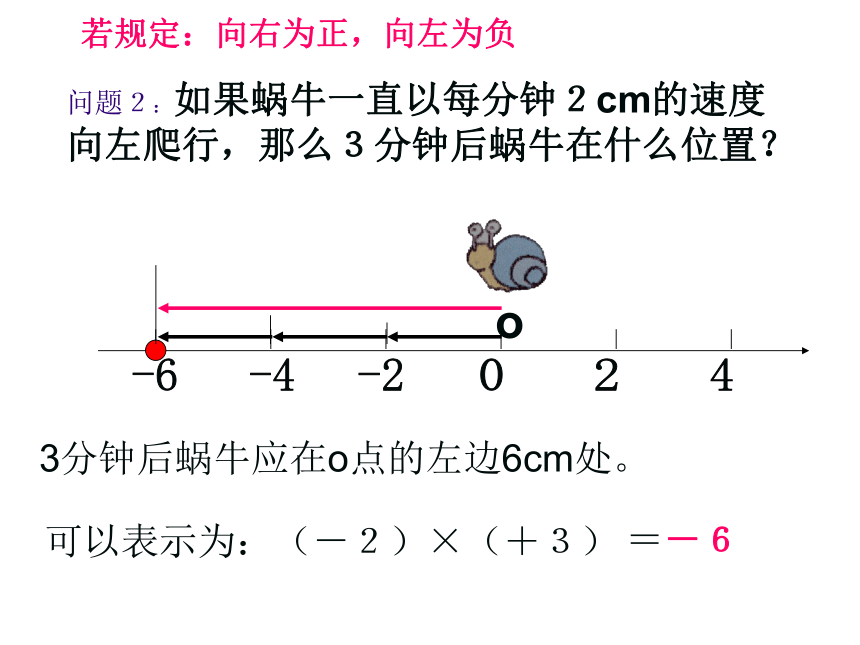
问题1:森林里住着一只蜗牛,每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的右边6cm处。o=+6可以表示为:(+2)×(+3)若规定:向右为正,向左为负问题2:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的左边6cm处。o=-6可以表示为:(-2)×(+3)若规定:向右为正,向左为负问题3:如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的左边6cm处。
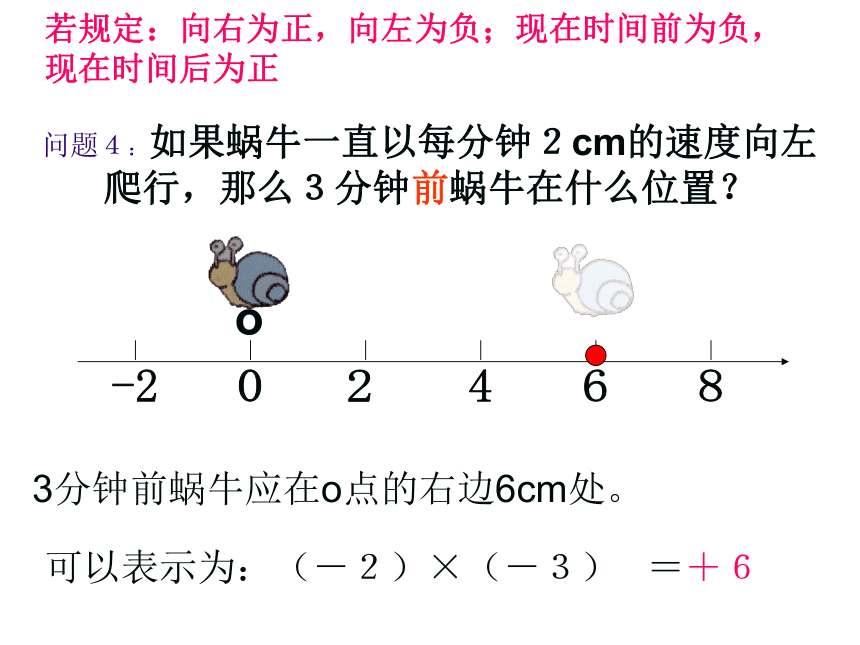
o=-6可以表示为:(+2)×(-3)若规定:向右为正,向左为负;现在时间前为负,现在时间后为正问题4:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的右边6cm处。o=+6可以表示为:(-2)×(-3)若规定:向右为正,向左为负;现在时间前为负,现在时间后为正仔细观察上面得到的四个式子:
(1)(+2)×(+3)=+6
(2)(-2)×3=-6
(3)(+2)×(-3)=-6
(4)(-2)×(-3)=+6
根据你对乘法的思考,你得到什么规律?总结规律有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与0相乘,积仍为0。你追我赶 : (抢答 ) 1、(-5)×(+3)= -15 2、(-5)×(-3)= +15 3、(-6)×(-4)= +24 4、(+4)×(-6)= -24 5、0×(-6)= 0水库水位的变化(?3)×4 = ?12(?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,第二个因数减少 1 时,积 怎么变化?36912 当第二个因数从 0 减少为 ?1时,
积从 增大为 ;积增大 3 。03结合法则,仔细观察下面两个式子:
(1) (-5)×(-2) = + (5×2) = +10;
(2) (-5) × 2 = — (5×2) = -10
同号两数相乘得正把绝对值相乘异号两数相乘得负把绝对值相乘理解法则,掌握实质步骤:(1)先确定积的符号;
(2)将每个因数的绝对值求积作为积的绝对值。
关键:确定积的符号 同号得正,异号得负巩固练习:
计算:(1)6×(-9)
(2)(-4)×6
(3)(-6)×(-1)
(4)(-6)×0
(5) ×(- )
(6)(- )×计算下列各题,并思考有什么特征: 新知拓展1×1 2× 3× (-4) (- ); (- ) (- )倒数:乘积是1的两个数互为倒数注意:正数的倒数是正数;负数的倒数是负数练习:1、求下列各数的倒数:
(1) - 3 (2)- 1 (3 ) -
(4) - 1 (5) 0.2 (6) 1.2分析:欲求某数的倒数,就是要确定与这个数相乘积为1的数是什么?求小数的倒数时,要先把小数化成分数;
求带分数的倒数时,要先把带分数化成假分数。注意:试一试:练习2:有一个简单的数值运算程序:输入xx乘以(-3)减2输出结果当输入的值为-1时,则输出的数值是: 1若输入的数值为(-7)呢?则输出的数值是19练习3 企业负债 某亏损企业,近十年来每年负债2万元,假定2004年底该企业的财产为0,照此计算:
(1)2007年底该企业的财产是多少?
(2)2001年底该企业的财产是多少?活学活用你一言我一语 这节课您有何收获?谢谢2006年9月20日 练习4、用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1千米,气温的变化量为-6℃,攀登3千米后,气温有什么变化?解: -6 ×3=-(6×3)=-18
答:气温下降18℃。
甲水库第一天
乙水库甲水库的水位每天升高3cm ,第二天第三天第四天乙水库的水位每天下降 3cm , 第一天 第二天 第三天 第四天4 天后,甲、乙水库各自水位的总变化 量是多少? 如果用正号表示水位的上升、用负号表示水位的下降。那么,4 天后,甲水库水位的总变化 量是:
乙水库水位的总变化 量是:3+3+3+3 = 3×4 = 12 (cm) ;(?3)+(?3)+(?3)+(?3) = (?3)×4 = ?12 (cm) ;水库水位的变化(?3)×4 = ?12(?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,第二个因数减少 1 时,积 怎么变化?引例1 蜗牛运动 设蜗牛现在的位置为点O,若它一直都是沿直线爬行,而且每分钟爬行2cm,问:
(1)向右爬行,3分钟后的位置?
(2)向左爬行,3分钟后的位置?
(3)向右爬行,3分钟前的位置?
(4)向左爬行,3分钟前的位置?
问题1:森林里住着一只蜗牛,每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的右边6cm处。o=+6可以表示为:(+2)×(+3)若规定:向右为正,向左为负问题2:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的左边6cm处。o=-6可以表示为:(-2)×(+3)若规定:向右为正,向左为负问题3:如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的左边6cm处。
o=-6可以表示为:(+2)×(-3)若规定:向右为正,向左为负;现在时间前为负,现在时间后为正问题4:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的右边6cm处。o=+6可以表示为:(-2)×(-3)若规定:向右为正,向左为负;现在时间前为负,现在时间后为正仔细观察上面得到的四个式子:
(1)(+2)×(+3)=+6
(2)(-2)×3=-6
(3)(+2)×(-3)=-6
(4)(-2)×(-3)=+6
根据你对乘法的思考,你得到什么规律?总结规律有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与0相乘,积仍为0。你追我赶 : (抢答 ) 1、(-5)×(+3)= -15 2、(-5)×(-3)= +15 3、(-6)×(-4)= +24 4、(+4)×(-6)= -24 5、0×(-6)= 0水库水位的变化(?3)×4 = ?12(?3)×3 = ,(?3)×2 = ,(?3)×1 = ,(?3)×0 = ,?9?6?30(?3)×(?1) = ,
(?3)×(?2) = ,
(?3)×(?3) = ,
(?3)×(?4) = ,第二个因数减少 1 时,积 怎么变化?36912 当第二个因数从 0 减少为 ?1时,
积从 增大为 ;积增大 3 。03结合法则,仔细观察下面两个式子:
(1) (-5)×(-2) = + (5×2) = +10;
(2) (-5) × 2 = — (5×2) = -10
同号两数相乘得正把绝对值相乘异号两数相乘得负把绝对值相乘理解法则,掌握实质步骤:(1)先确定积的符号;
(2)将每个因数的绝对值求积作为积的绝对值。
关键:确定积的符号 同号得正,异号得负巩固练习:
计算:(1)6×(-9)
(2)(-4)×6
(3)(-6)×(-1)
(4)(-6)×0
(5) ×(- )
(6)(- )×计算下列各题,并思考有什么特征: 新知拓展1×1 2× 3× (-4) (- ); (- ) (- )倒数:乘积是1的两个数互为倒数注意:正数的倒数是正数;负数的倒数是负数练习:1、求下列各数的倒数:
(1) - 3 (2)- 1 (3 ) -
(4) - 1 (5) 0.2 (6) 1.2分析:欲求某数的倒数,就是要确定与这个数相乘积为1的数是什么?求小数的倒数时,要先把小数化成分数;
求带分数的倒数时,要先把带分数化成假分数。注意:试一试:练习2:有一个简单的数值运算程序:输入xx乘以(-3)减2输出结果当输入的值为-1时,则输出的数值是: 1若输入的数值为(-7)呢?则输出的数值是19练习3 企业负债 某亏损企业,近十年来每年负债2万元,假定2004年底该企业的财产为0,照此计算:
(1)2007年底该企业的财产是多少?
(2)2001年底该企业的财产是多少?活学活用你一言我一语 这节课您有何收获?谢谢2006年9月20日 练习4、用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1千米,气温的变化量为-6℃,攀登3千米后,气温有什么变化?解: -6 ×3=-(6×3)=-18
答:气温下降18℃。
