专题5—指数函数、对数函数-近8年高考真题分类汇编—2023届高三数学一轮复习
文档属性
| 名称 | 专题5—指数函数、对数函数-近8年高考真题分类汇编—2023届高三数学一轮复习 |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:46:26 | ||
图片预览



文档简介
专题5—指数函数、对数函数
考试说明:1、了解指数函数模型的实际背景;
理解指数函数的概念,理解指数函数的单调性,掌握指数函数的图像通过特殊点;
理解对数函数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用;
理解对数函数的概念,理解对数函数的单调性,掌握对数函数图像通过的特殊点。
知道指数函数、对数函数是一类重要的函数模型。
高频考点:1、指数幂、对数式的化简与求值;
指数函数、对数函数的图像与性质的应用;
指数函数、对数函数的综合应用问题。
指数函数、对数函数是非常重要的基本函数,是高考中的高频考点,在选择题、填空题中考查其基本性质,在大题中,与导数结合的解答题年年必考。
典例分析
1.(2019 新课标Ⅰ)已知,,,则
A. B. C. D.
2.(2013 重庆)函数的定义域为
A. B. C.,, D.,,
3.(2019 北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是,则太阳与天狼星的亮度的比值为
A. B.10.1 C. D.
4.(2020 新课标Ⅲ)已知,.设,,,则
A. B. C. D.
5.(2016 新课标Ⅰ)若,,则
A. B. C. D.
6.(2016 新课标Ⅱ)下列函数中,其定义域和值域分别与函数的定义域和值域相同的是
A. B. C. D.
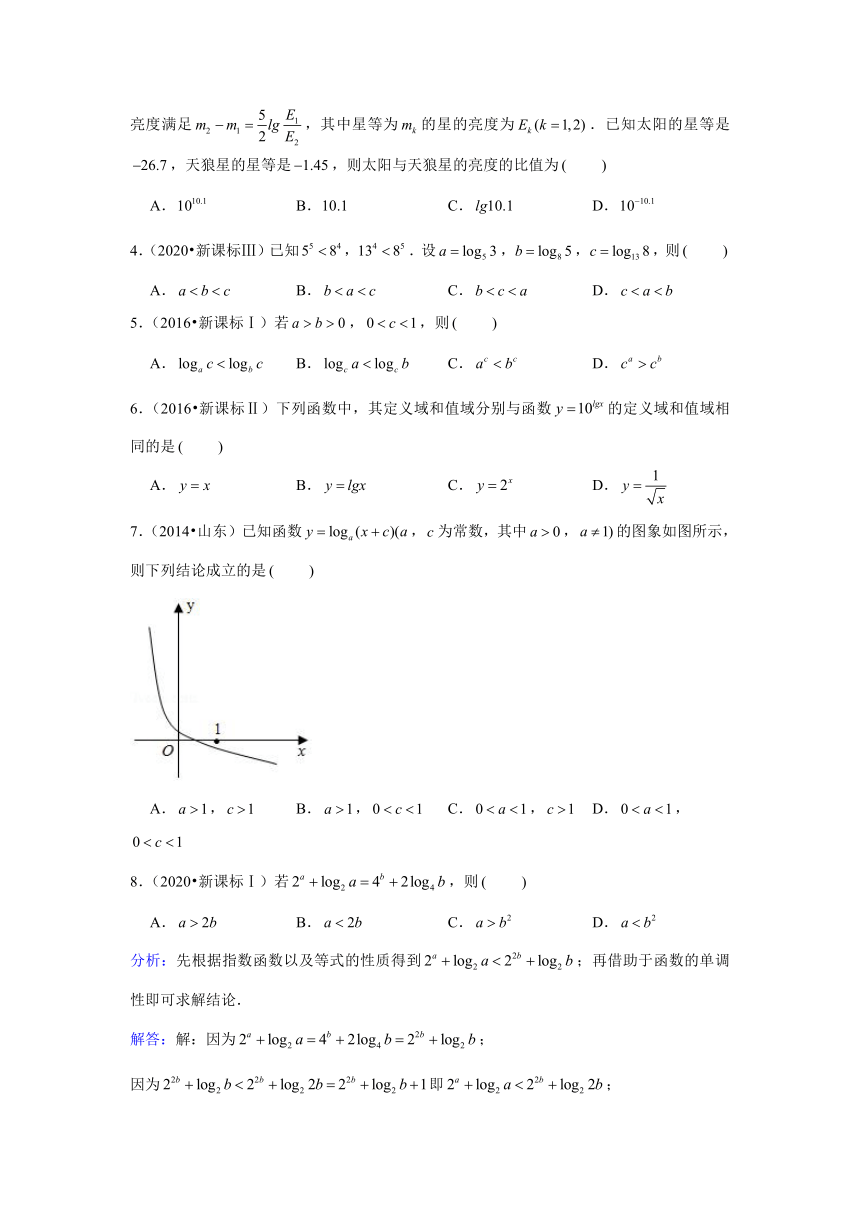
7.(2014 山东)已知函数,为常数,其中,的图象如图所示,则下列结论成立的是
A., B., C., D.,
8.(2020 新课标Ⅰ)若,则
A. B. C. D.
分析:先根据指数函数以及等式的性质得到;再借助于函数的单调性即可求解结论.
解答:解:因为;
因为即;
令,由指对数函数的单调性可得在内单调递增;
且(a);
故选:.
点评:本题主要考查指数函数和对数函数的应用,属于基础题.
9.(2014 山东)已知实数,满足,则下列关系式恒成立的是
A. B.
C. D.
分析:本题主要考查不等式的大小比较,利用函数的单调性的性质是解决本题的关键.
解答:解:实数,满足,,
.当时,,恒成立,
.当,时,满足,但不成立.
.若,则等价为成立,当,时,满足,但不成立.
.若,则等价为,即,当,时,满足,但不成立.
故选:.
点评:本题主要考查函数值的大小比较,利用不等式的性质以及函数的单调性是解决本题的关键.
真题集训
1.(2020 新课标Ⅲ)设,,,则
A. B. C. D.
2.(2018 新课标Ⅲ)设,,则
A. B. C. D.
3.(2016 全国)若函数,且的最大值与最小值之和为3,则
A.9 B.7 C.6 D.5
4.(2017 全国)设,则
A. B.
C. D.
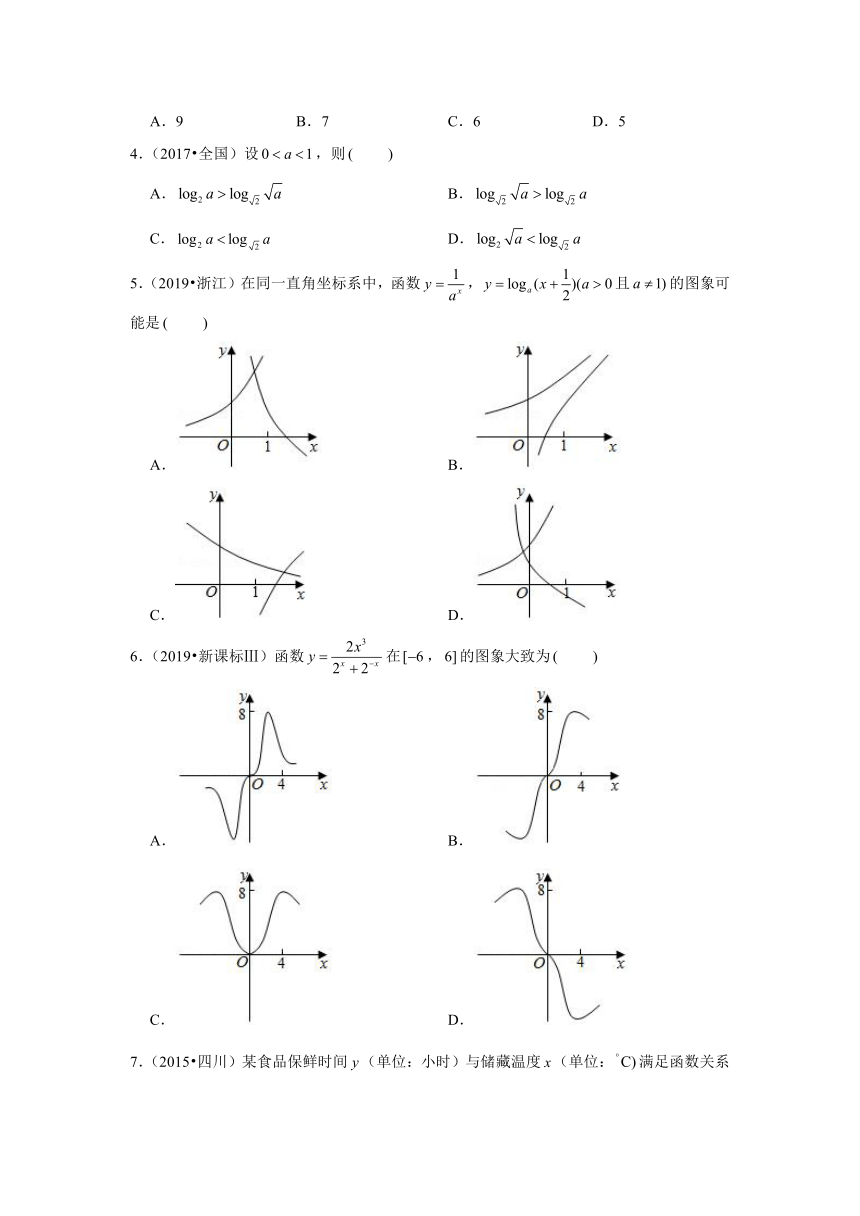
5.(2019 浙江)在同一直角坐标系中,函数,且的图象可能是
A. B.
C. D.
6.(2019 新课标Ⅲ)函数在,的图象大致为
A. B.
C. D.
7.(2015 四川)某食品保鲜时间(单位:小时)与储藏温度(单位:满足函数关系为自然对数的底数,,为常数).若该食品在的保鲜时间是192小时,在的保鲜时间是48小时,则该食品在的保鲜时间是
A.16小时 B.20小时 C.24小时 D.28小时
8.(2014 山东)已知实数,满足,则下列关系式恒成立的是
A. B.
C. D.
9.(2018 新课标Ⅰ)已知函数,若(3),则 .
10.(2013 北京)函数的值域为 .
11.(2015 福建)若函数且的值域是,,则实数的取值范围是 .
12.(2014 重庆)函数的最小值为 .
典例分析答案
1.(2019 新课标Ⅰ)已知,,,则
A. B. C. D.
分析:由指数函数和对数函数的单调性易得,,,从而得出,,的大小关系.
解答:解:,
,
,
,
,
故选:.
点评:本题考查了指数函数和对数函数的单调性,增函数和减函数的定义,属基础题.
2.(2013 重庆)函数的定义域为
A. B. C.,, D.,,
分析:根据“让解析式有意义”的原则,对数的真数大于0,分母不等于0,建立不等式,解之即可.
解答:解:要使原函数有意义,则,
解得:,或
所以原函数的定义域为,,.
故选:.
点评:本题主要考查了函数的定义域及其求法,求定义域常用的方法就是根据“让解析式有意义”的原则,属于基础题.
3.(2019 北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是,则太阳与天狼星的亮度的比值为
A. B.10.1 C. D.
分析:把已知熟记代入,化简后利用对数的运算性质求解.
解答:解:设太阳的星等是,天狼星的星等是,
由题意可得:,
,则.
故选:.
点评:本题考查对数的运算性质,是基础的计算题.
4.(2020 新课标Ⅲ)已知,.设,,,则
A. B. C. D.
分析:利用中间值比较即可,,根据由和,得到,即可确定,,的大小关系.
解答:解:由,
,而
,
即;
,,,;
,,,,
综上,.
故选:.
点评:本题考查了三个数大小的判断,指数对的运算和基本不等式的应用,考查了转化思想,是基础题.
5.(2016 新课标Ⅰ)若,,则
A. B. C. D.
分析:根据指数函数,对数函数,幂函数的单调性结合换底公式,逐一分析四个结论的真假,可得答案.
解答:解:,,
,故正确;
当时,
,故错误;
,故错误;
,故错误;
故选:.
点评:本题考查的知识点是指数函数,对数函数,幂函数的单调性,难度中档.
6.(2016 新课标Ⅱ)下列函数中,其定义域和值域分别与函数的定义域和值域相同的是
A. B. C. D.
分析:分别求出各个函数的定义域和值域,比较后可得答案.
解答:解:函数的定义域和值域均为,
函数的定义域和值域均为,不满足要求;
函数的定义域为,值域为,不满足要求;
函数的定义域为,值域为,不满足要求;
函数的定义域和值域均为,满足要求;
故选:.
点评:本题考查的知识点是函数的定义域和值域,熟练掌握各种基本初等函数的定义域和值域,是解答的关键.
7.(2014 山东)已知函数,为常数,其中,的图象如图所示,则下列结论成立的是
A., B., C., D.,
分析:根据对数函数的图象和性质即可得到结论.
解答:解:函数单调递减,,
当时,即,即,
当时,即,即,
故选:.
点评:本题主要考查对数函数的图象和性质,利用对数函数的单调性是解决本题的关键,比较基础.
8.(2020 新课标Ⅰ)若,则
A. B. C. D.
分析:先根据指数函数以及等式的性质得到;再借助于函数的单调性即可求解结论.
解答:解:因为;
因为即;
令,由指对数函数的单调性可得在内单调递增;
且(a);
故选:.
点评:本题主要考查指数函数和对数函数的应用,属于基础题.
9.(2014 山东)已知实数,满足,则下列关系式恒成立的是
A. B.
C. D.
分析:本题主要考查不等式的大小比较,利用函数的单调性的性质是解决本题的关键.
解答:解:实数,满足,,
.当时,,恒成立,
.当,时,满足,但不成立.
.若,则等价为成立,当,时,满足,但不成立.
.若,则等价为,即,当,时,满足,但不成立.
故选:.
点评:本题主要考查函数值的大小比较,利用不等式的性质以及函数的单调性是解决本题的关键.
真题集训 答案
1.解:,
,
,
.
故选:.
2.解:,,
,
,
,,
.
故选:.
3.解:函数且在,上单调,
当时,;当时,.则,
两边同时平方得:,.
故选:.
4.解:,,
在中,,故错误;
在 中,,故正确;
在中,,故错误;
在中,,故错误.
故选:.
5.解:由函数,,
当时,可得是递减函数,图象恒过点,
函数,是递增函数,图象恒过,;
当时,可得是递增函数,图象恒过点,
函数,是递减函数,图象恒过,;
满足要求的图象为:
故选:.
6.解:由在,,知
,
是,上的奇函数,因此排除
又(4),因此排除,.
故选:.
7.解:为自然对数的底数,,为常数).
当时,,
当时,
当时,
故选:.
8.解:实数,满足,
,
.取,,不成立;
.取,,不成立
.取,,不成立;
.由于在上单调递增,因此正确
故选:.
9.解:函数,若(3),
可得:,可得.
故答案为:.
10.解:当时,;
当时,.
所以函数的值域为.
故答案为.
11.解:由于函数且的值域是,,
故当时,满足.
①若,在它的定义域上单调递增,
当时,由,,,.
②若,在它的定义域上单调递减,
,不满足的值域是,.
综上可得,,
故答案为:,.
12.解:
,
当
即时,函数的最小值是.
故答案为:
考试说明:1、了解指数函数模型的实际背景;
理解指数函数的概念,理解指数函数的单调性,掌握指数函数的图像通过特殊点;
理解对数函数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用;
理解对数函数的概念,理解对数函数的单调性,掌握对数函数图像通过的特殊点。
知道指数函数、对数函数是一类重要的函数模型。
高频考点:1、指数幂、对数式的化简与求值;
指数函数、对数函数的图像与性质的应用;
指数函数、对数函数的综合应用问题。
指数函数、对数函数是非常重要的基本函数,是高考中的高频考点,在选择题、填空题中考查其基本性质,在大题中,与导数结合的解答题年年必考。
典例分析
1.(2019 新课标Ⅰ)已知,,,则
A. B. C. D.
2.(2013 重庆)函数的定义域为
A. B. C.,, D.,,
3.(2019 北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是,则太阳与天狼星的亮度的比值为
A. B.10.1 C. D.
4.(2020 新课标Ⅲ)已知,.设,,,则
A. B. C. D.
5.(2016 新课标Ⅰ)若,,则
A. B. C. D.
6.(2016 新课标Ⅱ)下列函数中,其定义域和值域分别与函数的定义域和值域相同的是
A. B. C. D.
7.(2014 山东)已知函数,为常数,其中,的图象如图所示,则下列结论成立的是
A., B., C., D.,
8.(2020 新课标Ⅰ)若,则
A. B. C. D.
分析:先根据指数函数以及等式的性质得到;再借助于函数的单调性即可求解结论.
解答:解:因为;
因为即;
令,由指对数函数的单调性可得在内单调递增;
且(a);
故选:.
点评:本题主要考查指数函数和对数函数的应用,属于基础题.
9.(2014 山东)已知实数,满足,则下列关系式恒成立的是
A. B.
C. D.
分析:本题主要考查不等式的大小比较,利用函数的单调性的性质是解决本题的关键.
解答:解:实数,满足,,
.当时,,恒成立,
.当,时,满足,但不成立.
.若,则等价为成立,当,时,满足,但不成立.
.若,则等价为,即,当,时,满足,但不成立.
故选:.
点评:本题主要考查函数值的大小比较,利用不等式的性质以及函数的单调性是解决本题的关键.
真题集训
1.(2020 新课标Ⅲ)设,,,则
A. B. C. D.
2.(2018 新课标Ⅲ)设,,则
A. B. C. D.
3.(2016 全国)若函数,且的最大值与最小值之和为3,则
A.9 B.7 C.6 D.5
4.(2017 全国)设,则
A. B.
C. D.
5.(2019 浙江)在同一直角坐标系中,函数,且的图象可能是
A. B.
C. D.
6.(2019 新课标Ⅲ)函数在,的图象大致为
A. B.
C. D.
7.(2015 四川)某食品保鲜时间(单位:小时)与储藏温度(单位:满足函数关系为自然对数的底数,,为常数).若该食品在的保鲜时间是192小时,在的保鲜时间是48小时,则该食品在的保鲜时间是
A.16小时 B.20小时 C.24小时 D.28小时
8.(2014 山东)已知实数,满足,则下列关系式恒成立的是
A. B.
C. D.
9.(2018 新课标Ⅰ)已知函数,若(3),则 .
10.(2013 北京)函数的值域为 .
11.(2015 福建)若函数且的值域是,,则实数的取值范围是 .
12.(2014 重庆)函数的最小值为 .
典例分析答案
1.(2019 新课标Ⅰ)已知,,,则
A. B. C. D.
分析:由指数函数和对数函数的单调性易得,,,从而得出,,的大小关系.
解答:解:,
,
,
,
,
故选:.
点评:本题考查了指数函数和对数函数的单调性,增函数和减函数的定义,属基础题.
2.(2013 重庆)函数的定义域为
A. B. C.,, D.,,
分析:根据“让解析式有意义”的原则,对数的真数大于0,分母不等于0,建立不等式,解之即可.
解答:解:要使原函数有意义,则,
解得:,或
所以原函数的定义域为,,.
故选:.
点评:本题主要考查了函数的定义域及其求法,求定义域常用的方法就是根据“让解析式有意义”的原则,属于基础题.
3.(2019 北京)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是,则太阳与天狼星的亮度的比值为
A. B.10.1 C. D.
分析:把已知熟记代入,化简后利用对数的运算性质求解.
解答:解:设太阳的星等是,天狼星的星等是,
由题意可得:,
,则.
故选:.
点评:本题考查对数的运算性质,是基础的计算题.
4.(2020 新课标Ⅲ)已知,.设,,,则
A. B. C. D.
分析:利用中间值比较即可,,根据由和,得到,即可确定,,的大小关系.
解答:解:由,
,而
,
即;
,,,;
,,,,
综上,.
故选:.
点评:本题考查了三个数大小的判断,指数对的运算和基本不等式的应用,考查了转化思想,是基础题.
5.(2016 新课标Ⅰ)若,,则
A. B. C. D.
分析:根据指数函数,对数函数,幂函数的单调性结合换底公式,逐一分析四个结论的真假,可得答案.
解答:解:,,
,故正确;
当时,
,故错误;
,故错误;
,故错误;
故选:.
点评:本题考查的知识点是指数函数,对数函数,幂函数的单调性,难度中档.
6.(2016 新课标Ⅱ)下列函数中,其定义域和值域分别与函数的定义域和值域相同的是
A. B. C. D.
分析:分别求出各个函数的定义域和值域,比较后可得答案.
解答:解:函数的定义域和值域均为,
函数的定义域和值域均为,不满足要求;
函数的定义域为,值域为,不满足要求;
函数的定义域为,值域为,不满足要求;
函数的定义域和值域均为,满足要求;
故选:.
点评:本题考查的知识点是函数的定义域和值域,熟练掌握各种基本初等函数的定义域和值域,是解答的关键.
7.(2014 山东)已知函数,为常数,其中,的图象如图所示,则下列结论成立的是
A., B., C., D.,
分析:根据对数函数的图象和性质即可得到结论.
解答:解:函数单调递减,,
当时,即,即,
当时,即,即,
故选:.
点评:本题主要考查对数函数的图象和性质,利用对数函数的单调性是解决本题的关键,比较基础.
8.(2020 新课标Ⅰ)若,则
A. B. C. D.
分析:先根据指数函数以及等式的性质得到;再借助于函数的单调性即可求解结论.
解答:解:因为;
因为即;
令,由指对数函数的单调性可得在内单调递增;
且(a);
故选:.
点评:本题主要考查指数函数和对数函数的应用,属于基础题.
9.(2014 山东)已知实数,满足,则下列关系式恒成立的是
A. B.
C. D.
分析:本题主要考查不等式的大小比较,利用函数的单调性的性质是解决本题的关键.
解答:解:实数,满足,,
.当时,,恒成立,
.当,时,满足,但不成立.
.若,则等价为成立,当,时,满足,但不成立.
.若,则等价为,即,当,时,满足,但不成立.
故选:.
点评:本题主要考查函数值的大小比较,利用不等式的性质以及函数的单调性是解决本题的关键.
真题集训 答案
1.解:,
,
,
.
故选:.
2.解:,,
,
,
,,
.
故选:.
3.解:函数且在,上单调,
当时,;当时,.则,
两边同时平方得:,.
故选:.
4.解:,,
在中,,故错误;
在 中,,故正确;
在中,,故错误;
在中,,故错误.
故选:.
5.解:由函数,,
当时,可得是递减函数,图象恒过点,
函数,是递增函数,图象恒过,;
当时,可得是递增函数,图象恒过点,
函数,是递减函数,图象恒过,;
满足要求的图象为:
故选:.
6.解:由在,,知
,
是,上的奇函数,因此排除
又(4),因此排除,.
故选:.
7.解:为自然对数的底数,,为常数).
当时,,
当时,
当时,
故选:.
8.解:实数,满足,
,
.取,,不成立;
.取,,不成立
.取,,不成立;
.由于在上单调递增,因此正确
故选:.
9.解:函数,若(3),
可得:,可得.
故答案为:.
10.解:当时,;
当时,.
所以函数的值域为.
故答案为.
11.解:由于函数且的值域是,,
故当时,满足.
①若,在它的定义域上单调递增,
当时,由,,,.
②若,在它的定义域上单调递减,
,不满足的值域是,.
综上可得,,
故答案为:,.
12.解:
,
当
即时,函数的最小值是.
故答案为:
同课章节目录
