专题15—解三角形(2)—平面几何中的问题-近8年高考真题分类汇编—2023届高三数学一轮复习
文档属性
| 名称 | 专题15—解三角形(2)—平面几何中的问题-近8年高考真题分类汇编—2023届高三数学一轮复习 |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:46:26 | ||
图片预览




文档简介
专题15—解三角形(2)—平面几何中的问题
考试说明:1、掌握正弦定理、余弦定理,并能解决一些简单的三角
形度量问题。
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何有关的实际问题
高频考点:1、边角的求解;
2、判断三角形的形状;
求与面积、范围有关的问题;
解决平面几何图形问题;
解决实际问题。
高考中,利用正弦、余弦定理解三角形问题是必考的,题型较多,有基础题,比如直接利用定理解三角形,也有难题,比如求范围的问题,出题比较灵活,一些同学总是掌握的不是很好,下面就近几年高考题,给大家分类整理各种题型,希望对大家有所帮助。
典例分析
题型二:解决平面几何中的问题
1.(2016 新课标Ⅲ)在中,,边上的高等于,则等于
A. B. C. D.
2.(2016 新课标Ⅲ)在中,,边上的高等于,则
A. B. C. D.
3.(2021 浙江)我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别为3,4,记大正方形的面积为,小正方形的面积为,则 25 .
4.(2017 浙江)已知,,,点为延长线上一点,,连结,则的面积是 , .
5.(2015 重庆)在中,,,的角平分线,则 .
6.(2015 新课标Ⅰ)在平面四边形中,.,则的取值范围是 , .
7.(2021 新高考Ⅰ)记的内角,,的对边分别为,,.已知,点在边上,.
(1)证明:;
(2)若,求.
8.(2020 江苏)在中,角、、的对边分别为、、.已知,,.
(1)求的值;
(2)在边上取一点,使得,求的值.
二、真题集训
1.(2021 浙江)在中,,,是的中点,,则 ; .
2.(2017 全国)在中,为的中点,,,,则 .
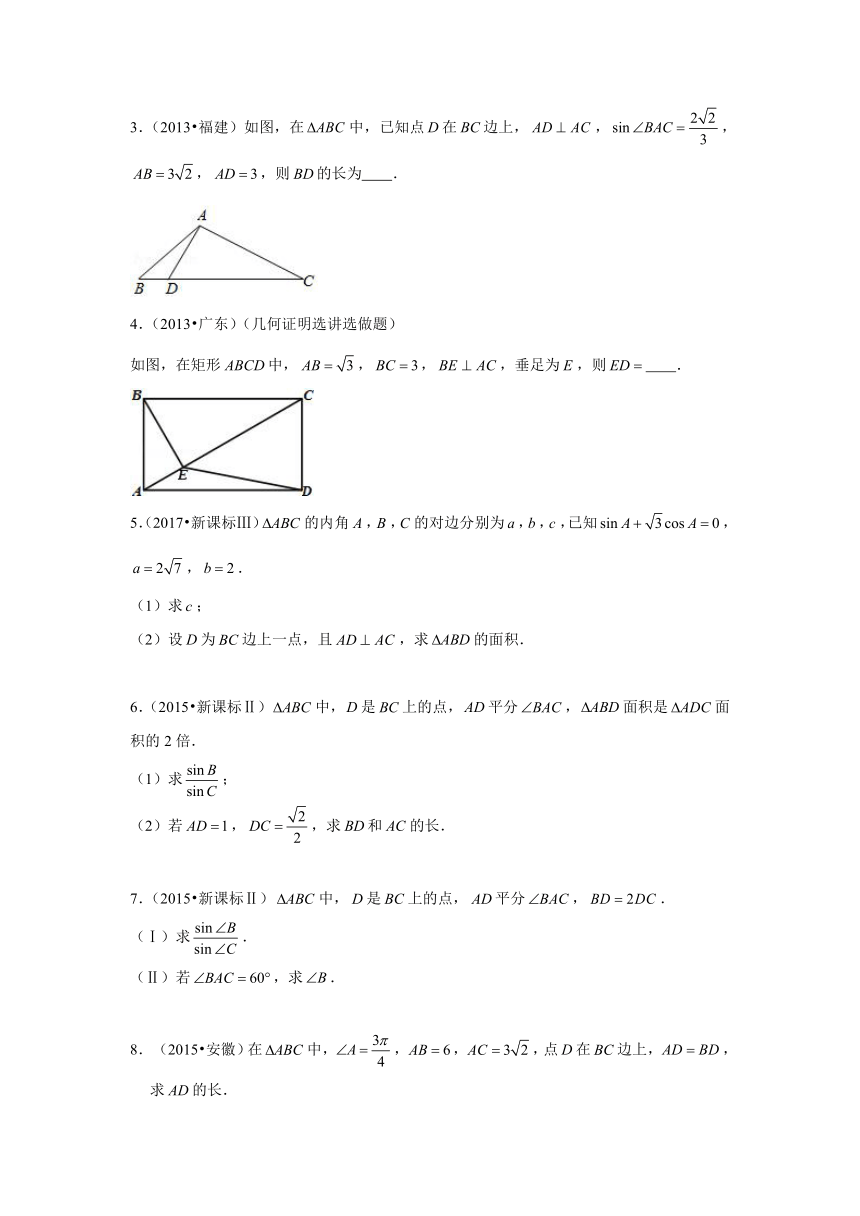
3.(2013 福建)如图,在中,已知点在边上,,,,,则的长为 .
4.(2013 广东)(几何证明选讲选做题)
如图,在矩形中,,,,垂足为,则 .
5.(2017 新课标Ⅲ)的内角,,的对边分别为,,,已知,,.
(1)求;
(2)设为边上一点,且,求的面积.
6.(2015 新课标Ⅱ)中,是上的点,平分,面积是面积的2倍.
(1)求;
(2)若,,求和的长.
7.(2015 新课标Ⅱ)中,是上的点,平分,.
(Ⅰ)求.
(Ⅱ)若,求.
(2015 安徽)在中,,,,点在边上,,求的长.
典例分析答案
题型二:解决平面几何中的问题
1.(2016 新课标Ⅲ)在中,,边上的高等于,则等于
A. B. C. D.
分析:作出图形,令,依题意,可求得,,利用两角和的余弦即可求得答案.
解答:解:设中角、、、对应的边分别为、、,于,令,
在中,,边上的高,
,,
在中,,故,
.
故选:.
点评:本题考查解三角形中,作出图形,令,利用两角和的余弦求是关键,也是亮点,属于中档题.
2.(2016 新课标Ⅲ)在中,,边上的高等于,则
A. B. C. D.
分析:由已知,结合勾股定理和余弦定理,求出,,再由三角形面积公式,可得.
解答:解:在中,,边上的高等于,
,
由余弦定理得:,
故,
,
故选:.
点评:本题考查的知识点是三角形中的几何计算,熟练掌握正弦定理和余弦定理,是解答的关键.
3.(2021 浙江)我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别为3,4,记大正方形的面积为,小正方形的面积为,则 25 .
分析:利用勾股定理求出直角三角形斜边长,即大正方形的边长,由,求出,再求出.
解答:解:直角三角形直角边的长分别为3,4,
直角三角形斜边的长为,
即大正方形的边长为5,,
则小正方形的面积,
.
故答案为:25.
点评:本题考查了三角形中的几何计算和勾股定理,考查运算能力,属于基础题.
4.(2017 浙江)已知,,,点为延长线上一点,,连结,则的面积是 , .
分析:如图,取得中点,根据勾股定理求出,再求出,再根据即可求出,根据等腰三角形的性质和二倍角公式即可求出
解答:解:如图,取得中点,
,,
,,
,
,
,
,
,
,
在中,
,
,
,
故答案为:,
点评:本题考查了解三角形的有关知识,关键是转化,属于基础题
5.(2015 重庆)在中,,,的角平分线,则 .
分析:利用已知条件求出,,然后利用正弦定理求出即可.
解答:解:由题意以及正弦定理可知:,即,,
,可得,则,三角形是等腰三角形,
.
故答案为:.
点评:本题考查正弦定理以及余弦定理的应用,三角形的解法,考查计算能力.
6.(2015 新课标Ⅰ)在平面四边形中,.,则的取值范围是 , .
分析:如图所示,延长,交于点,设,,,,求出,即可求出的取值范围.
解答:解:方法一:
如图所示,延长,交于点,则
在中,,,,
设,,,,
,
,
,
,
而,
的取值范围是,.
故答案为:,.
方法二:
如下图,作出底边的等腰三角形,,
倾斜角为的直线在平面内移动,分别交、于、,则四边形即为满足题意的四边形;
当直线移动时,运用极限思想,
①直线接近点时,趋近最小,为;
②直线接近点时,趋近最大值,为;
故答案为:,.
点评:本题考查求的取值范围,考查三角形中的几何计算,考查学生的计算能力,属于中档题.
7.(2021 新高考Ⅰ)记的内角,,的对边分别为,,.已知,点在边上,.
(1)证明:;
(2)若,求.
分析:(1)利用正弦定理求解;
(2)要能找到隐含条件:和互补,从而列出等式关系求解.
解答:解:(1)证明:由正弦定理知,,
,,
,,
即,
,
;
(2)法一:由(1)知,
,,,
在中,由余弦定理知,,
在中,由余弦定理知,,
,
,
即,
得,
,
,
或,
在中,由余弦定理知,,
当时,(舍;
当时,;
综上所述,.
法二:点在边上且,
,
,
而由(1)知,
,
即,
由余弦定理知:,
,
,
,
或,
在中,由余弦定理知,,
当时,(舍;
当时,;
综上所述,.
点评:本题考查正弦定理及余弦定理的内容,是一道好题.
8.(2020 江苏)在中,角、、的对边分别为、、.已知,,.
(1)求的值;
(2)在边上取一点,使得,求的值.
分析:(1)由题意及余弦定理求出边,再由正弦定理求出的值;
(2)三角形的内角和为,,可得为钝角,可得与互为补角,所以展开可得及,进而求出的值.
解答:解:(1)因为,,.,由余弦定理可得:,
由正弦定理可得,所以,
所以;
(2)因为,所以,
在三角形 中,易知为锐角,由(1)可得,
所以在三角形中,,
因为,所以,
所以.
点评:本题考查三角形的正弦定理及余弦定理的应用,及两角和的正弦公式的应用,属于中档题.
真题集训答案
1.解:在中:,,,解得:或(舍去).
点是中点,,,在中:,;
在中:.
故答案为:;.
2.解:在中,为的中点,,,,
可得,
平方可得,
即为,
可得,
可得为直角三角形,且,
则,
故答案为:10.
3.解:,,
,
,
在中,,,
根据余弦定理得:,
则.
故答案为:
4.解:矩形,,
在中,,,根据勾股定理得:,
,即,,
,
在中,,,
根据余弦定理得:,
则.
故答案为:
5.解:(1),
,
,
,
由余弦定理可得,
即,
即,
解得(舍去)或,
故.
(2),
,
,
,
6.解:(1)如图,过作于,
,
平分
在中,,
在中,,;
.分
(2)由(1)知,.
过作于,作于,
平分,
,
,
,
令,则,
,
,
由余弦定理可得:,
,
,
的长为,的长为1.
7.解:(Ⅰ)如图,
由正弦定理得:
,
平分,,
;
(Ⅱ),,
,
由(Ⅰ)知,
,即.
8.解:,,,
在中,由余弦定理可得:.
分
在中,由正弦定理可得:,
,
分
过点作的垂线,垂足为,由得:,
中,分
考试说明:1、掌握正弦定理、余弦定理,并能解决一些简单的三角
形度量问题。
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何有关的实际问题
高频考点:1、边角的求解;
2、判断三角形的形状;
求与面积、范围有关的问题;
解决平面几何图形问题;
解决实际问题。
高考中,利用正弦、余弦定理解三角形问题是必考的,题型较多,有基础题,比如直接利用定理解三角形,也有难题,比如求范围的问题,出题比较灵活,一些同学总是掌握的不是很好,下面就近几年高考题,给大家分类整理各种题型,希望对大家有所帮助。
典例分析
题型二:解决平面几何中的问题
1.(2016 新课标Ⅲ)在中,,边上的高等于,则等于
A. B. C. D.
2.(2016 新课标Ⅲ)在中,,边上的高等于,则
A. B. C. D.
3.(2021 浙江)我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别为3,4,记大正方形的面积为,小正方形的面积为,则 25 .
4.(2017 浙江)已知,,,点为延长线上一点,,连结,则的面积是 , .
5.(2015 重庆)在中,,,的角平分线,则 .
6.(2015 新课标Ⅰ)在平面四边形中,.,则的取值范围是 , .
7.(2021 新高考Ⅰ)记的内角,,的对边分别为,,.已知,点在边上,.
(1)证明:;
(2)若,求.
8.(2020 江苏)在中,角、、的对边分别为、、.已知,,.
(1)求的值;
(2)在边上取一点,使得,求的值.
二、真题集训
1.(2021 浙江)在中,,,是的中点,,则 ; .
2.(2017 全国)在中,为的中点,,,,则 .
3.(2013 福建)如图,在中,已知点在边上,,,,,则的长为 .
4.(2013 广东)(几何证明选讲选做题)
如图,在矩形中,,,,垂足为,则 .
5.(2017 新课标Ⅲ)的内角,,的对边分别为,,,已知,,.
(1)求;
(2)设为边上一点,且,求的面积.
6.(2015 新课标Ⅱ)中,是上的点,平分,面积是面积的2倍.
(1)求;
(2)若,,求和的长.
7.(2015 新课标Ⅱ)中,是上的点,平分,.
(Ⅰ)求.
(Ⅱ)若,求.
(2015 安徽)在中,,,,点在边上,,求的长.
典例分析答案
题型二:解决平面几何中的问题
1.(2016 新课标Ⅲ)在中,,边上的高等于,则等于
A. B. C. D.
分析:作出图形,令,依题意,可求得,,利用两角和的余弦即可求得答案.
解答:解:设中角、、、对应的边分别为、、,于,令,
在中,,边上的高,
,,
在中,,故,
.
故选:.
点评:本题考查解三角形中,作出图形,令,利用两角和的余弦求是关键,也是亮点,属于中档题.
2.(2016 新课标Ⅲ)在中,,边上的高等于,则
A. B. C. D.
分析:由已知,结合勾股定理和余弦定理,求出,,再由三角形面积公式,可得.
解答:解:在中,,边上的高等于,
,
由余弦定理得:,
故,
,
故选:.
点评:本题考查的知识点是三角形中的几何计算,熟练掌握正弦定理和余弦定理,是解答的关键.
3.(2021 浙江)我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别为3,4,记大正方形的面积为,小正方形的面积为,则 25 .
分析:利用勾股定理求出直角三角形斜边长,即大正方形的边长,由,求出,再求出.
解答:解:直角三角形直角边的长分别为3,4,
直角三角形斜边的长为,
即大正方形的边长为5,,
则小正方形的面积,
.
故答案为:25.
点评:本题考查了三角形中的几何计算和勾股定理,考查运算能力,属于基础题.
4.(2017 浙江)已知,,,点为延长线上一点,,连结,则的面积是 , .
分析:如图,取得中点,根据勾股定理求出,再求出,再根据即可求出,根据等腰三角形的性质和二倍角公式即可求出
解答:解:如图,取得中点,
,,
,,
,
,
,
,
,
,
在中,
,
,
,
故答案为:,
点评:本题考查了解三角形的有关知识,关键是转化,属于基础题
5.(2015 重庆)在中,,,的角平分线,则 .
分析:利用已知条件求出,,然后利用正弦定理求出即可.
解答:解:由题意以及正弦定理可知:,即,,
,可得,则,三角形是等腰三角形,
.
故答案为:.
点评:本题考查正弦定理以及余弦定理的应用,三角形的解法,考查计算能力.
6.(2015 新课标Ⅰ)在平面四边形中,.,则的取值范围是 , .
分析:如图所示,延长,交于点,设,,,,求出,即可求出的取值范围.
解答:解:方法一:
如图所示,延长,交于点,则
在中,,,,
设,,,,
,
,
,
,
而,
的取值范围是,.
故答案为:,.
方法二:
如下图,作出底边的等腰三角形,,
倾斜角为的直线在平面内移动,分别交、于、,则四边形即为满足题意的四边形;
当直线移动时,运用极限思想,
①直线接近点时,趋近最小,为;
②直线接近点时,趋近最大值,为;
故答案为:,.
点评:本题考查求的取值范围,考查三角形中的几何计算,考查学生的计算能力,属于中档题.
7.(2021 新高考Ⅰ)记的内角,,的对边分别为,,.已知,点在边上,.
(1)证明:;
(2)若,求.
分析:(1)利用正弦定理求解;
(2)要能找到隐含条件:和互补,从而列出等式关系求解.
解答:解:(1)证明:由正弦定理知,,
,,
,,
即,
,
;
(2)法一:由(1)知,
,,,
在中,由余弦定理知,,
在中,由余弦定理知,,
,
,
即,
得,
,
,
或,
在中,由余弦定理知,,
当时,(舍;
当时,;
综上所述,.
法二:点在边上且,
,
,
而由(1)知,
,
即,
由余弦定理知:,
,
,
,
或,
在中,由余弦定理知,,
当时,(舍;
当时,;
综上所述,.
点评:本题考查正弦定理及余弦定理的内容,是一道好题.
8.(2020 江苏)在中,角、、的对边分别为、、.已知,,.
(1)求的值;
(2)在边上取一点,使得,求的值.
分析:(1)由题意及余弦定理求出边,再由正弦定理求出的值;
(2)三角形的内角和为,,可得为钝角,可得与互为补角,所以展开可得及,进而求出的值.
解答:解:(1)因为,,.,由余弦定理可得:,
由正弦定理可得,所以,
所以;
(2)因为,所以,
在三角形 中,易知为锐角,由(1)可得,
所以在三角形中,,
因为,所以,
所以.
点评:本题考查三角形的正弦定理及余弦定理的应用,及两角和的正弦公式的应用,属于中档题.
真题集训答案
1.解:在中:,,,解得:或(舍去).
点是中点,,,在中:,;
在中:.
故答案为:;.
2.解:在中,为的中点,,,,
可得,
平方可得,
即为,
可得,
可得为直角三角形,且,
则,
故答案为:10.
3.解:,,
,
,
在中,,,
根据余弦定理得:,
则.
故答案为:
4.解:矩形,,
在中,,,根据勾股定理得:,
,即,,
,
在中,,,
根据余弦定理得:,
则.
故答案为:
5.解:(1),
,
,
,
由余弦定理可得,
即,
即,
解得(舍去)或,
故.
(2),
,
,
,
6.解:(1)如图,过作于,
,
平分
在中,,
在中,,;
.分
(2)由(1)知,.
过作于,作于,
平分,
,
,
,
令,则,
,
,
由余弦定理可得:,
,
,
的长为,的长为1.
7.解:(Ⅰ)如图,
由正弦定理得:
,
平分,,
;
(Ⅱ),,
,
由(Ⅰ)知,
,即.
8.解:,,,
在中,由余弦定理可得:.
分
在中,由正弦定理可得:,
,
分
过点作的垂线,垂足为,由得:,
中,分
同课章节目录
