(2022秋季新教材)人教版 五年级数学上册6.1 平行四边形的面积(一)课件(共22张PPT)
文档属性
| 名称 | (2022秋季新教材)人教版 五年级数学上册6.1 平行四边形的面积(一)课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 21:22:26 | ||
图片预览







文档简介
(共22张PPT)
2
0
2
2
2022秋人教版数学五年级上册
平行四边形的面积 (1)
人教版数学五年级上册 第六单元
课堂小结
基础练习
情景导入
探究新知
(二)提出问题:
这节课我们就来一起学习平行四边形的面积。
回忆一下,我们是用什么方法得出长方形的面积的计算公式的?
(一)出示情景:
情景导入
我只会算长方形的……
(一)借助方格,初步探究
1. 我特别想知道你们是怎么得到这个结论的,谁来说说你是怎
么数的?
2. 有没有不同的方法?有什么办法能帮助我们数得更快一些呢?
3. 这种“一剪一拼”的方法,我们称为“割补”法。
组织研讨:
在方格纸上数一数,然后填写下表。(一个方格代表1m ,不满一格的都按半格计算。)
不数方格,能不能计算平行四边形的面积呢?
探究新知
你发现了什么?
(二)借助图形,深入探究
1. 提出问题:
(2)回忆一下,长方形面积和谁有关系?
(1)如果没有方格纸,拿到这样一个平行四边形,我们怎么研究
它的面积?
我们有这样的经验:在研究一个不知道的新问题时,我们可以把它转化成以前学过的知识,利用旧知识来解决新问题。今天要研究平行四边形的面积,我们是不是可以借助这个经验把它转化成学过的图形?
探究新知
(3)长、宽中任意一个变化,都会导致长方形面积发生变化。由此你猜测一下,平行四边形的面积可能会和谁有关系呢?
平行四边形的面积与底(高)究竟有怎样的关系?看来仅仅知道结论是不行的,我们得进一步研究,怎么研究呢?
探究新知
(二)借助图形,深入探究
请同学们根据前面的经验,两人一组,借助你们手中的平行四边形纸,可以画一画,剪一剪,拼一拼,看看能不能找到转化前后图形间的联系,并把你找到的联系在纸上写一写,让别人一眼就能看出你是如何推导出平行四边形面积计算方法的。
探究新知
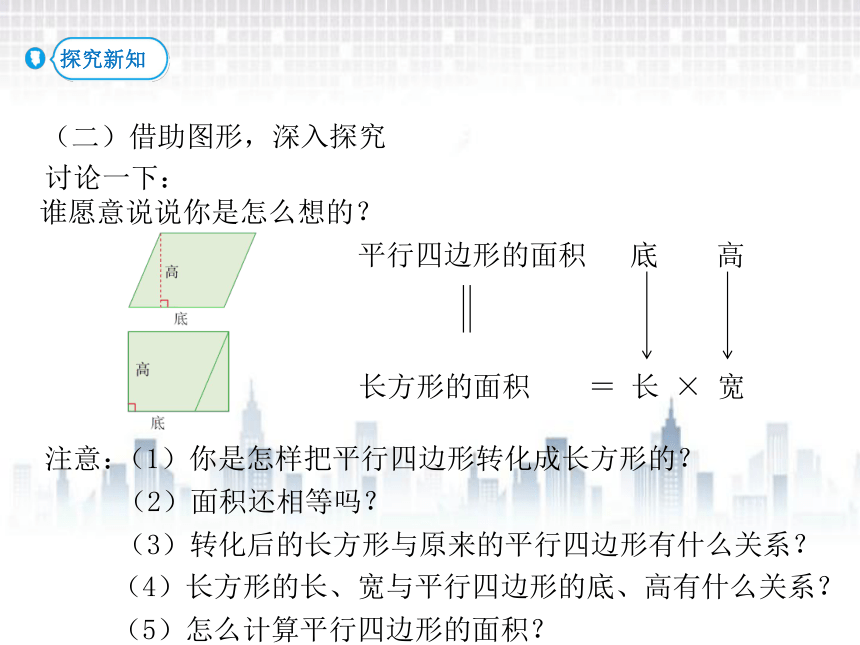
(二)借助图形,深入探究
讨论一下:
谁愿意说说你是怎么想的?
注意:
(1)你是怎样把平行四边形转化成长方形的?
(2)面积还相等吗?
(3)转化后的长方形与原来的平行四边形有什么关系?
(4)长方形的长、宽与平行四边形的底、高有什么关系?
(5)怎么计算平行四边形的面积?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
探究新知
探究新知
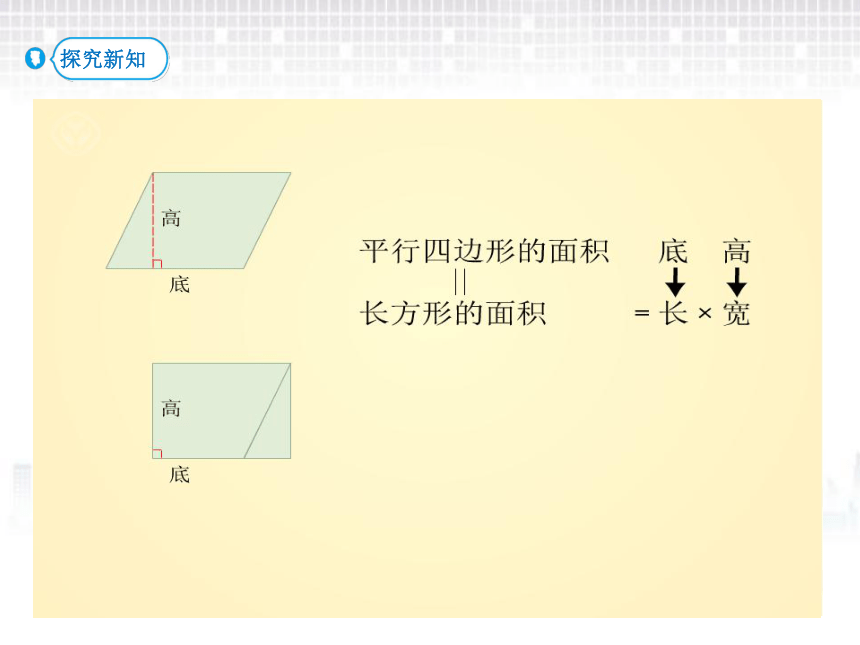
(二)借助图形,深入探究
还有不同的转化方法吗?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
注意:
你能从这个图形中找到转化图形前后之间的联系,
也推出底×高吗?
讨论一下:
探究新知
探究新知
(二)借助图形,深入探究
还有不同的转化方法吗?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
注意:
这样也完成了将新图形转化成旧图形的任务,你能找到它与原来平行四边形之间的关系,推出面积的计算公式吗?
讨论一下:
探究新知
探究新知
4. 归纳概括,总结方法:
(二)借助图形,深入探究
刚才同学们都是沿着平行四边形的高把它分成两部分或三部分,然后通过平移把平行四边形转化成一个长方形。
探究新知
现在能说说怎么计算平行四边形的面积吗?
平行四边形的面积=底×高
出示字母公式:
如果用S 表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的 高,平行四边形的面积计算公式可以写成: S= ɑh。
探究新知
(二)借助图形,深入探究
回忆一下,刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
探究新知
(1)首先是把新图形转化成了旧图形,我们是如何转化的?
(2)然后找到新旧图形之间的联系,这个联系不能仅仅是局部的,还是整体的联系。
(3)最后推导出新图形的面积公式。
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
探究新知
1. 平行四边形花坛的底是6 m,高是4 m,它的面积是多少?
S=ɑh
=6×4
=24(m2)
答:它的面积是24 m2。
基础练习
2. 计算下面每个平行四边形的面积。
3.下面图中两个平行四边形的面积相等吗?它们的面积各是多少?
基础练习
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2
0
2
2
2022秋人教版数学五年级上册
平行四边形的面积 (1)
人教版数学五年级上册 第六单元
课堂小结
基础练习
情景导入
探究新知
(二)提出问题:
这节课我们就来一起学习平行四边形的面积。
回忆一下,我们是用什么方法得出长方形的面积的计算公式的?
(一)出示情景:
情景导入
我只会算长方形的……
(一)借助方格,初步探究
1. 我特别想知道你们是怎么得到这个结论的,谁来说说你是怎
么数的?
2. 有没有不同的方法?有什么办法能帮助我们数得更快一些呢?
3. 这种“一剪一拼”的方法,我们称为“割补”法。
组织研讨:
在方格纸上数一数,然后填写下表。(一个方格代表1m ,不满一格的都按半格计算。)
不数方格,能不能计算平行四边形的面积呢?
探究新知
你发现了什么?
(二)借助图形,深入探究
1. 提出问题:
(2)回忆一下,长方形面积和谁有关系?
(1)如果没有方格纸,拿到这样一个平行四边形,我们怎么研究
它的面积?
我们有这样的经验:在研究一个不知道的新问题时,我们可以把它转化成以前学过的知识,利用旧知识来解决新问题。今天要研究平行四边形的面积,我们是不是可以借助这个经验把它转化成学过的图形?
探究新知
(3)长、宽中任意一个变化,都会导致长方形面积发生变化。由此你猜测一下,平行四边形的面积可能会和谁有关系呢?
平行四边形的面积与底(高)究竟有怎样的关系?看来仅仅知道结论是不行的,我们得进一步研究,怎么研究呢?
探究新知
(二)借助图形,深入探究
请同学们根据前面的经验,两人一组,借助你们手中的平行四边形纸,可以画一画,剪一剪,拼一拼,看看能不能找到转化前后图形间的联系,并把你找到的联系在纸上写一写,让别人一眼就能看出你是如何推导出平行四边形面积计算方法的。
探究新知
(二)借助图形,深入探究
讨论一下:
谁愿意说说你是怎么想的?
注意:
(1)你是怎样把平行四边形转化成长方形的?
(2)面积还相等吗?
(3)转化后的长方形与原来的平行四边形有什么关系?
(4)长方形的长、宽与平行四边形的底、高有什么关系?
(5)怎么计算平行四边形的面积?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
探究新知
探究新知
(二)借助图形,深入探究
还有不同的转化方法吗?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
注意:
你能从这个图形中找到转化图形前后之间的联系,
也推出底×高吗?
讨论一下:
探究新知
探究新知
(二)借助图形,深入探究
还有不同的转化方法吗?
长方形的面积 = 长 × 宽
平行四边形的面积 底 高
注意:
这样也完成了将新图形转化成旧图形的任务,你能找到它与原来平行四边形之间的关系,推出面积的计算公式吗?
讨论一下:
探究新知
探究新知
4. 归纳概括,总结方法:
(二)借助图形,深入探究
刚才同学们都是沿着平行四边形的高把它分成两部分或三部分,然后通过平移把平行四边形转化成一个长方形。
探究新知
现在能说说怎么计算平行四边形的面积吗?
平行四边形的面积=底×高
出示字母公式:
如果用S 表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的 高,平行四边形的面积计算公式可以写成: S= ɑh。
探究新知
(二)借助图形,深入探究
回忆一下,刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
探究新知
(1)首先是把新图形转化成了旧图形,我们是如何转化的?
(2)然后找到新旧图形之间的联系,这个联系不能仅仅是局部的,还是整体的联系。
(3)最后推导出新图形的面积公式。
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
探究新知
1. 平行四边形花坛的底是6 m,高是4 m,它的面积是多少?
S=ɑh
=6×4
=24(m2)
答:它的面积是24 m2。
基础练习
2. 计算下面每个平行四边形的面积。
3.下面图中两个平行四边形的面积相等吗?它们的面积各是多少?
基础练习
Thank you for listening
感谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
