2022-2023学年高一数学同步优品讲练课件人教A版(2019)必修 第一册 1.1 集合的概念 (共32张PPT)
文档属性
| 名称 | 2022-2023学年高一数学同步优品讲练课件人教A版(2019)必修 第一册 1.1 集合的概念 (共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 22:32:50 | ||
图片预览











文档简介
(共32张PPT)
第一章 集合与常用逻辑用语
1.1 集合的概念
榆次一中 数学教研组
学习目标
1.了解集合的含义,体会元素与集合的关系,能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用.(数学抽象)
2.了解集合中元素的确定性、互异性、无序性,掌握常用数集及其专用符号,并能够用其解决有关问题,提高学生分析问题和解决问题的能力,培养学生的应用意识.(逻辑推理)
3.掌握集合的两种常用表示方法(列举法和描述法).(数学抽象)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
1.回忆一下初中实数的分类.
[答案] 分为有理数和无理数,或正数、零和负数.
2.1是整数吗?
[答案] 1是整数;
3.
[答案]
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
4.在生活中,有许多事物给我们以集体的印象,比如,你的家庭,你所在的班级,山东省的所有城市,等等,你还能举出一些这样的例子吗?
[答案] 冬奥会的参赛项目,东昌湖中的鱼,济南动物园中的老虎,构成英文单词“
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 育才中学今年入学的爱好数学的学生可以组成一个集合.( )
×
(2) 元素 , , 和元素 , ,1组成的集合是相等的.( )
√
(3) 方程 的所有解的集合可表示为 .( )
×
(4) 集合 不能用列举法表示.( )
√
自学检测
2.用描述法表示函数 图象上的所有点,其中正确的是( @9@ ).
A. B.
C. D.
C
[解析] 该集合是点集,故可表示为 .故选C.
3.方程 与方程 的所有解组成的集合中共有____个元素.
2
[解析] 由 ,得 ;由 ,得 ,故集合中只有2个元素1和 .
4.下列元素与集合的关系判断正确的是_______.(填序号)
① ;② ;③ ;④ ;⑤ .
①④
[解析] 表示自然数集, 表示有理数集, 表示整数集, 表示实数集,故 , , , , .
探究1 集合的概念
9月1日晚上,学校通知:全体高一学生6点钟开始在班级进行开学教育,之后“偶数班”去一楼大厅领取数学教辅书《导学案》.
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题1:.这个通知的对象有哪些?
[答案] 高一全体学生;“偶数班”.
问题2:.这些对象能构成一个集合吗?
[答案] 能.
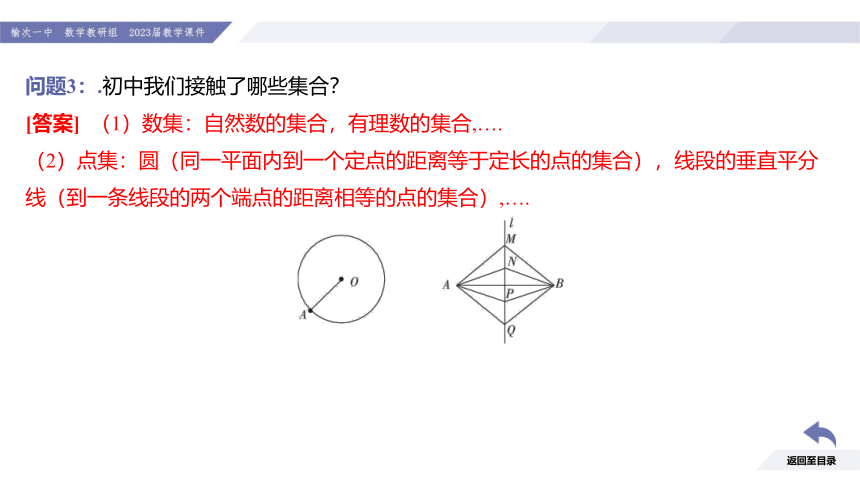
问题3:.初中我们接触了哪些集合?
[答案] (1)数集:自然数的集合,有理数的集合,….
(2)点集:圆(同一平面内到一个定点的距离等于定长的点的集合),线段的垂直平分线(到一条线段的两个端点的距离相等的点的集合),….
新知生成
1.元素与集合的概念
(1)元素:一般地,我们把___________统称为元素.元素通常用小写拉丁字母 , , ,表示.
(2)集合:把一些元素组成的_______叫作集合(简称为_____).集合通常用大写拉丁字母 , , 表示.
(3)集合相等:只要构成两个集合的_______是一样的,我们就称这两个集合是相等的.
2.集合中元素的三个特性
确定性、无序性、互异性.
研究对象
总体
集
元素
新知运用
例1
(1) 下列元素的全体能组成集合的是( @22@ ).
A.著名数学家 B.很大的数
C.聪明的人 D.小于3的实数
(2)判断下列元素的全体能否组成集合.①不超过20的非负数;②方程 在实数范围内的解;③某校2021年在校的所有高个子同学;④ 的近似值的全体.
D
[解析] (1)只有选项D有明确的标准,能组成一个集合,故选D.
(2)①对任意一个实数能判断出是不是“不超过20的非负数”,所以能组成集合;
②能组成集合;
③“高个子”无明确的标准,对于某个人算不算高个子无法客观地判断,因此不能组成集合;
④“ 的近似值”没有明确精确到什么程度,因此不能判断一个数是不是它的近似值,所以不能组成集合.
方法指导 根据集合的定义判断.
1.(多选题)下列各组对象能组成集合的是( @24@ ).
A.2022年北京冬奥会的5个冰上项目和10个雪上项目
B.高中数学的所有难题
C.被3除余2的所有整数
D.函数 图象上所有的点
ACD
[解析] 选项A, , 中的元素符合集合中元素的确定性;而选项B中,“难题”没有明确标准,不符合集合中元素的确定性,不能构成集合.
巩固训练
2.下列每组对象,能组成一个集合的是_______.
①一中高一年级聪明的学生;②平面直角坐标系中横、纵坐标相等的点;③不小于3的正整数.
②③
[解析] ①“一中高一年级聪明的学生”的标准不确定,不能构成集合;②“平面直角坐标系中横、纵坐标相等的点”的标准确定,能构成集合;③“不小于3的正整数”的标准确定,能构成集合.
探究2 元素与集合的关系
把高一年级所有的同学组成的集合记为
问题1:.请问
[答案]
问题2:.由
[答案] 由
问题3:.问题2中
[答案] 因为
情境设置
新知生成
1.元素与集合的关系:如果 是集合 中的元素,就说 _______集合 ,记作 ;如果 不是集合 中的元素,就说 _________集合 ,记作________.
2.常用的数集及其记法
常用的数集 自然数集 正整数集 整数集 有理数集 实数集
记法 ____ ___________ ____ ____ ____
3.
属于
不属于
新知运用
例2
(1) 下列五个关系中,正确的个数为( @39@ ).
① ;② ;③ ;④ ;⑤ .
A. B. C. D.
C
[解析] 由于 , , 是无理数,故①②⑤正确,因为 是无理数, 是自然数,所以③④错误.故选C.
(2) 若集合 中的元素 满足 , ,则集合 中的元素为_____________.
[解析] 由题意可得 为自然数,所以 可以为2, , ,对应的 的值为0, , ,因此 中元素为0, , .
方法总结 判断元素与集合关系的两种方法:(1)直接法,若集合中的元素是直接给出的,则只要判断该元素在已知集合中是否出现即可.(2)推理法,对于一些没有直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可,此时应首先明确已知集合中的元素具有什么特征.
已知集合 中有两个元素 , ,若 ,则实数 的值为____.
1
[解析] , 或 .
当 时, ,此时 , 中元素重复,不符合题意.
当 时, 或 (舍去), ,此时, ,符合题意.
巩固训练
探究3 集合的表示方法
开学第一天学习了集合,老师布置了一道作业:把所有满足不等式
姓名 答案
王浩宇
李琦
张瑜
谢芳
情境设置
问题1:.王浩宇的答案是否正确?他用了什么方法表示?
[答案] 正确,他是先解不等式,再找出正整数解,最后用列举法表示.
问题2:.小组讨论李琦、张瑜、谢芳三位同学的答案有几个是正确的.
[答案] 李琦和谢芳的答案都是正确的,用描述法要注意花括号内用一竖杠分开,竖杠左边的是元素,竖杠右边的是元素满足的条件.
问题3:.任何一个集合是否既能用列举法也能用描述法表示 若不能,举例说明.
[答案] 不一定,一般有有限个元素的集合或有无限个元素且元素之间有明显规律的集合可用列举法表示,而有无限个元素且元素间无规律可循的集合不能用列举法表示,如不等式
新知生成
集合常用的表示法
(1)_________:在花括号内把集合的所有元素一一列举出来,特点是_____________________________.
(2)_________:用集合中元素的属性表示集合,其一般形式是_____________________.
列举法
适用于元素的个数较少的集合
描述法
新知运用
一、用列举法表示集合
例3 用列举法表示下列集合:
(1)2022年北京张家口冬奥会所有冰上项目组成的集合;
(2)单词“
(3)所有正整数组成的集合;
(4)直线
[解析] (1)冰上项目有五个,所求集合用列举法表示为 冰壶,冰球,速度滑冰,短道速滑,花样滑冰 .
(2)单词“ ”中有两个互不相同的字母,分别为“ ”“ ”,所求集合用列举法表示为 .
(3)正整数为1, , , ,所求集合用列举法表示为 .
(4)方程组 的解是 所求集合用列举法表示为 .
方法总结 用列举法表示集合的步骤及注意点
(1)分清元素:用列举法表示集合,要分清是数集还是点集,或是其他元素.
(2)书写集合:列元素时要做到不重复、不遗漏.
提醒:二元方程组的解集、函数的图象上的点形成的集合都是点的集合,一定要写成有序实数对的形式,元素与元素之间用“,”隔开.如
二、用描述法表示集合
例4 用描述法表示下列集合:
(1)函数
(2)数轴上离原点的距离大于3的点组成的集合;
(3)不等式
[解析] (1) .
(2)数轴上离原点的距离大于3的点组成的集合等于绝对值大于3的实数组成的集合,则数轴上离原点的距离大于3的点组成的集合用描述法表示为 .
(3)不等式 的解是 ,则不等式 的解组成的集合用描述法表示为 .
方法总结 用描述法表示集合的2个步骤
1.集合 用列举法表示为( @54@ ).
A. B. C. D.
A
[解析] 解方程 得 或 ,集合用列举法表示为 .
2.方程组 的解集不能表示为( @56@ ).
A. B.
C. D.
C
[解析] 二元一次方程组的解是一个有序实数对,故C错误.
巩固训练
1.下列各组对象可以组成集合的是( @58@ ).
A.数学必修1课本中所有的难题 B.小于8的所有素数
C.直角坐标平面内第一象限的一些点 D.所有小的正数
B
[解析] 中“难题”的标准不确定,不能构成集合; 能构成集合; 中“一些点”无明确的标准,不能构成集合; 中“小”没有明确的标准,不能构成集合.
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.若 , , , 为集合 的四个元素,则以 , , , 为边长构成的四边形可能是
( @60@ ).
A.矩形 B.平行四边形 C.菱形 D.梯形
D
[解析] 由集合中的元素具有互异性可知 , , , 互不相等,而梯形的四条边可以互不相等,故选D.
3.已知集合 中元素 满足 ,且 ,又集合 中恰有三个元素,则整数 ____.
6
[解析] , ,且集合 中恰有三个元素, .
4.用适当的方法表示下列集合:
(1)绝对值不大于3的偶数的集合;
(2)被3除余1的正整数的集合;
(3)一次函数
[解析] (1)用列举法表示为 .
(2)用描述法表示为 .
(3)用描述法表示为 .
第一章 集合与常用逻辑用语
1.1 集合的概念
榆次一中 数学教研组
学习目标
1.了解集合的含义,体会元素与集合的关系,能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用.(数学抽象)
2.了解集合中元素的确定性、互异性、无序性,掌握常用数集及其专用符号,并能够用其解决有关问题,提高学生分析问题和解决问题的能力,培养学生的应用意识.(逻辑推理)
3.掌握集合的两种常用表示方法(列举法和描述法).(数学抽象)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
1.回忆一下初中实数的分类.
[答案] 分为有理数和无理数,或正数、零和负数.
2.1是整数吗?
[答案] 1是整数;
3.
[答案]
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
4.在生活中,有许多事物给我们以集体的印象,比如,你的家庭,你所在的班级,山东省的所有城市,等等,你还能举出一些这样的例子吗?
[答案] 冬奥会的参赛项目,东昌湖中的鱼,济南动物园中的老虎,构成英文单词“
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 育才中学今年入学的爱好数学的学生可以组成一个集合.( )
×
(2) 元素 , , 和元素 , ,1组成的集合是相等的.( )
√
(3) 方程 的所有解的集合可表示为 .( )
×
(4) 集合 不能用列举法表示.( )
√
自学检测
2.用描述法表示函数 图象上的所有点,其中正确的是( @9@ ).
A. B.
C. D.
C
[解析] 该集合是点集,故可表示为 .故选C.
3.方程 与方程 的所有解组成的集合中共有____个元素.
2
[解析] 由 ,得 ;由 ,得 ,故集合中只有2个元素1和 .
4.下列元素与集合的关系判断正确的是_______.(填序号)
① ;② ;③ ;④ ;⑤ .
①④
[解析] 表示自然数集, 表示有理数集, 表示整数集, 表示实数集,故 , , , , .
探究1 集合的概念
9月1日晚上,学校通知:全体高一学生6点钟开始在班级进行开学教育,之后“偶数班”去一楼大厅领取数学教辅书《导学案》.
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题1:.这个通知的对象有哪些?
[答案] 高一全体学生;“偶数班”.
问题2:.这些对象能构成一个集合吗?
[答案] 能.
问题3:.初中我们接触了哪些集合?
[答案] (1)数集:自然数的集合,有理数的集合,….
(2)点集:圆(同一平面内到一个定点的距离等于定长的点的集合),线段的垂直平分线(到一条线段的两个端点的距离相等的点的集合),….
新知生成
1.元素与集合的概念
(1)元素:一般地,我们把___________统称为元素.元素通常用小写拉丁字母 , , ,表示.
(2)集合:把一些元素组成的_______叫作集合(简称为_____).集合通常用大写拉丁字母 , , 表示.
(3)集合相等:只要构成两个集合的_______是一样的,我们就称这两个集合是相等的.
2.集合中元素的三个特性
确定性、无序性、互异性.
研究对象
总体
集
元素
新知运用
例1
(1) 下列元素的全体能组成集合的是( @22@ ).
A.著名数学家 B.很大的数
C.聪明的人 D.小于3的实数
(2)判断下列元素的全体能否组成集合.①不超过20的非负数;②方程 在实数范围内的解;③某校2021年在校的所有高个子同学;④ 的近似值的全体.
D
[解析] (1)只有选项D有明确的标准,能组成一个集合,故选D.
(2)①对任意一个实数能判断出是不是“不超过20的非负数”,所以能组成集合;
②能组成集合;
③“高个子”无明确的标准,对于某个人算不算高个子无法客观地判断,因此不能组成集合;
④“ 的近似值”没有明确精确到什么程度,因此不能判断一个数是不是它的近似值,所以不能组成集合.
方法指导 根据集合的定义判断.
1.(多选题)下列各组对象能组成集合的是( @24@ ).
A.2022年北京冬奥会的5个冰上项目和10个雪上项目
B.高中数学的所有难题
C.被3除余2的所有整数
D.函数 图象上所有的点
ACD
[解析] 选项A, , 中的元素符合集合中元素的确定性;而选项B中,“难题”没有明确标准,不符合集合中元素的确定性,不能构成集合.
巩固训练
2.下列每组对象,能组成一个集合的是_______.
①一中高一年级聪明的学生;②平面直角坐标系中横、纵坐标相等的点;③不小于3的正整数.
②③
[解析] ①“一中高一年级聪明的学生”的标准不确定,不能构成集合;②“平面直角坐标系中横、纵坐标相等的点”的标准确定,能构成集合;③“不小于3的正整数”的标准确定,能构成集合.
探究2 元素与集合的关系
把高一年级所有的同学组成的集合记为
问题1:.请问
[答案]
问题2:.由
[答案] 由
问题3:.问题2中
[答案] 因为
情境设置
新知生成
1.元素与集合的关系:如果 是集合 中的元素,就说 _______集合 ,记作 ;如果 不是集合 中的元素,就说 _________集合 ,记作________.
2.常用的数集及其记法
常用的数集 自然数集 正整数集 整数集 有理数集 实数集
记法 ____ ___________ ____ ____ ____
3.
属于
不属于
新知运用
例2
(1) 下列五个关系中,正确的个数为( @39@ ).
① ;② ;③ ;④ ;⑤ .
A. B. C. D.
C
[解析] 由于 , , 是无理数,故①②⑤正确,因为 是无理数, 是自然数,所以③④错误.故选C.
(2) 若集合 中的元素 满足 , ,则集合 中的元素为_____________.
[解析] 由题意可得 为自然数,所以 可以为2, , ,对应的 的值为0, , ,因此 中元素为0, , .
方法总结 判断元素与集合关系的两种方法:(1)直接法,若集合中的元素是直接给出的,则只要判断该元素在已知集合中是否出现即可.(2)推理法,对于一些没有直接表示的集合,只要判断该元素是否满足集合中元素所具有的特征即可,此时应首先明确已知集合中的元素具有什么特征.
已知集合 中有两个元素 , ,若 ,则实数 的值为____.
1
[解析] , 或 .
当 时, ,此时 , 中元素重复,不符合题意.
当 时, 或 (舍去), ,此时, ,符合题意.
巩固训练
探究3 集合的表示方法
开学第一天学习了集合,老师布置了一道作业:把所有满足不等式
姓名 答案
王浩宇
李琦
张瑜
谢芳
情境设置
问题1:.王浩宇的答案是否正确?他用了什么方法表示?
[答案] 正确,他是先解不等式,再找出正整数解,最后用列举法表示.
问题2:.小组讨论李琦、张瑜、谢芳三位同学的答案有几个是正确的.
[答案] 李琦和谢芳的答案都是正确的,用描述法要注意花括号内用一竖杠分开,竖杠左边的是元素,竖杠右边的是元素满足的条件.
问题3:.任何一个集合是否既能用列举法也能用描述法表示 若不能,举例说明.
[答案] 不一定,一般有有限个元素的集合或有无限个元素且元素之间有明显规律的集合可用列举法表示,而有无限个元素且元素间无规律可循的集合不能用列举法表示,如不等式
新知生成
集合常用的表示法
(1)_________:在花括号内把集合的所有元素一一列举出来,特点是_____________________________.
(2)_________:用集合中元素的属性表示集合,其一般形式是_____________________.
列举法
适用于元素的个数较少的集合
描述法
新知运用
一、用列举法表示集合
例3 用列举法表示下列集合:
(1)2022年北京张家口冬奥会所有冰上项目组成的集合;
(2)单词“
(3)所有正整数组成的集合;
(4)直线
[解析] (1)冰上项目有五个,所求集合用列举法表示为 冰壶,冰球,速度滑冰,短道速滑,花样滑冰 .
(2)单词“ ”中有两个互不相同的字母,分别为“ ”“ ”,所求集合用列举法表示为 .
(3)正整数为1, , , ,所求集合用列举法表示为 .
(4)方程组 的解是 所求集合用列举法表示为 .
方法总结 用列举法表示集合的步骤及注意点
(1)分清元素:用列举法表示集合,要分清是数集还是点集,或是其他元素.
(2)书写集合:列元素时要做到不重复、不遗漏.
提醒:二元方程组的解集、函数的图象上的点形成的集合都是点的集合,一定要写成有序实数对的形式,元素与元素之间用“,”隔开.如
二、用描述法表示集合
例4 用描述法表示下列集合:
(1)函数
(2)数轴上离原点的距离大于3的点组成的集合;
(3)不等式
[解析] (1) .
(2)数轴上离原点的距离大于3的点组成的集合等于绝对值大于3的实数组成的集合,则数轴上离原点的距离大于3的点组成的集合用描述法表示为 .
(3)不等式 的解是 ,则不等式 的解组成的集合用描述法表示为 .
方法总结 用描述法表示集合的2个步骤
1.集合 用列举法表示为( @54@ ).
A. B. C. D.
A
[解析] 解方程 得 或 ,集合用列举法表示为 .
2.方程组 的解集不能表示为( @56@ ).
A. B.
C. D.
C
[解析] 二元一次方程组的解是一个有序实数对,故C错误.
巩固训练
1.下列各组对象可以组成集合的是( @58@ ).
A.数学必修1课本中所有的难题 B.小于8的所有素数
C.直角坐标平面内第一象限的一些点 D.所有小的正数
B
[解析] 中“难题”的标准不确定,不能构成集合; 能构成集合; 中“一些点”无明确的标准,不能构成集合; 中“小”没有明确的标准,不能构成集合.
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.若 , , , 为集合 的四个元素,则以 , , , 为边长构成的四边形可能是
( @60@ ).
A.矩形 B.平行四边形 C.菱形 D.梯形
D
[解析] 由集合中的元素具有互异性可知 , , , 互不相等,而梯形的四条边可以互不相等,故选D.
3.已知集合 中元素 满足 ,且 ,又集合 中恰有三个元素,则整数 ____.
6
[解析] , ,且集合 中恰有三个元素, .
4.用适当的方法表示下列集合:
(1)绝对值不大于3的偶数的集合;
(2)被3除余1的正整数的集合;
(3)一次函数
[解析] (1)用列举法表示为 .
(2)用描述法表示为 .
(3)用描述法表示为 .
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
