2022-2023学年高一数学同步优品讲练课件(人教A版2019必修第一册)1.4 充分条件与必要条件-(共32张PPT)
文档属性
| 名称 | 2022-2023学年高一数学同步优品讲练课件(人教A版2019必修第一册)1.4 充分条件与必要条件-(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 22:36:35 | ||
图片预览











文档简介
(共32张PPT)
第一章 集合与常用逻辑用语
1.4 充分条件与必要条件
榆次一中 数学教研组
学习目标
1.理解充分条件、必要条件、充要条件的概念.(数学抽象)
2.了解充分条件与判定定理,必要条件与性质定理,充要条件与性质定理的关系.(逻辑推理)
3.能通过充分性、必要性解决简单的问题.(逻辑推理)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
1.初中我们学过的命题的定义是什么?
[答案] 判断一件事的语句.
2.命题的常用形式是什么?
[答案] 数学中的命题常可以写成“如果……那么……”的形式.
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
3.何为真命题?何为假命题?
[答案] 如果题设成立,那么结论一定成立的命题为真命题,结论不能保证一定成立的为假命题.
4.命题“若
[答案] 充分条件.
5.命题“若
[答案] 不充分条件.
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 如果 是 的必要条件,那么 是唯一的.( )
×
(2) 是 的必要条件的含义是:如果 不成立,那么 一定不成立.( )
√
(3) “ ”是“ , 都大于0”成立的充分条件.( )
×
(4) 若 是 的充分条件,则 是 的必要条件.( )
√
自学检测
2.(多选题)下列条件中是 的充分条件的是( @10@ ).
A. B. C. D.
BCD
[解析] 当 时, ,但 ,故A错误,B,C,D都正确.
3.若 , ,则 是 的_______条件.(填“充分”“必要”或“充要”)
必要
[解析] ,即 ,故 是 的必要条件.
4.若 是 的充要条件, 是 的充要条件,则 是 的_______条件.(填“充分”“必要”或“充要”)
充要
[解析] 依题意, , ,所以 .
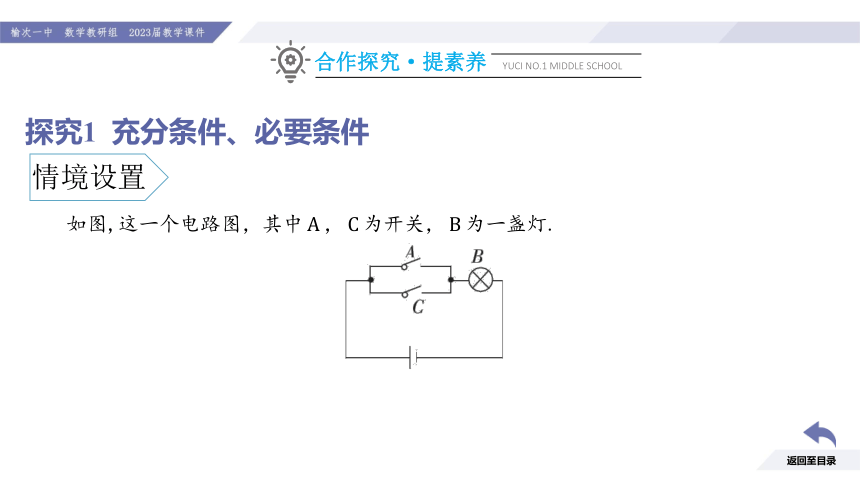
探究1 充分条件、必要条件
如图,这一个电路图,其中
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题1:.
[答案] 一定.
问题2:.
[答案] 不一定.
问题3:.
[答案] 充分条件.
新知生成
1.命题的概念及结构
(1) 一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫作_______.判断为真的语句是_________,判断为假的语句是_________.
命题
真命题
假命题
(2) 当命题表示为“若 ,则 ”时,____是命题的条件,____是命题的结论.
2.充分条件与必要条件
一般地,“若 ,则 ”为_________,是指由 通过推理可以得出 .这时,我们就说,由 可以推出 ,记作 ,并且说, 是 的___________, 是 的___________.
如果“若 ,则 ”为假命题,那么由条件 不能推出结论 ,记作 .此时,我们就说 不是 的___________, 不是 的___________.
真命题
充分条件
必要条件
充分条件
必要条件
特别提醒:
1.
(1)“若
(2)由条件
(3)
(4)只要有条件
(5)为得到结论
显然,
(1)所谓充分,就是说条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证的.“有之必成立,无之未必不成立”.
(2)充分条件不是唯一的,如
2.对充分条件的理解
新知运用
一、必要条件
例1 下列“若
(1)若一个四边形是等腰梯形,则这个四边形的两条对角线相等;
(2)若
(3)若
(4)若关于
[解析] (1)等腰梯形的两条对角线相等,因此 ,所以 是 的必要条件.
(2)直角三角形不一定是等腰三角形,因此 ,所以 不是 的必要条件.
(3)命题“若 ,则 ”是真命题,因此 ,所以 是 的必要条件.
(4)命题“若关于 的方程 有唯一解,则 ”为假命题,因此 ,所以 不是 的必要条件.
方法总结 必要条件的两种判断方法
(1)定义法:
(2)命题判断法:
若命题“若
二、充分条件
例2 下列“若
(1)若
(2)若
(3)若
(4)若
(5)在
(6)若四边形
[解析] (1)因为 ,所以 ,所以 是 的充分条件.
(2)因为 ,所以 .因此 ,所以 是 的充分条件.
(3)若 , ,则 ,但 ,所以 ,所以 不是 的充分条件.
(4)由 可以推出 或 ,不一定有 ,因此 ,所以 不是 的充分条件.
(5)由三角形中大角对大边可知,若 ,则 ,因此 ,所以 是 的充分条件.
(6)由菱形和正方形的定义可知,所有的正方形都是菱形,所以 ,所以 是 的充分条件.
方法总结 充分条件的两种判断方法
(1)定义法:
(2)命题判断法:
若命题“若
1.设集合 , ,则“ ”是“ ”的_______条件.(填“充分”或“必要”)
必要
[解析] 因为集合 , ,当 时, .因为“ ” “ ”,但“ ” “ ”,所以“ ”是“ ”的必要条件.
2.设集合 , ,那么“ ”是“ ”的_______条件.(填“充分”或“必要”)
充分
[解析] 由题意得 ,所以“ ” “ ”,所以“ ”是“ ”的充分条件.
巩固训练
探究2 充要条件
老张邀请张三、李四、王五三个人吃饭,时间到了,只有张三、李四准时赴约,王五因事不能到场,老张说:“该来的没有来.”张三听了脸色一沉,起来一声不吭地走了.老张愣了片刻,又道了句:“不该走的又走了.”李四听了大怒,拂袖而去.
问题1:.张三为什么走了?
[答案] “该来的没有来”的等价命题是“来了的都不该来”,张三觉得自己是不该来的.
情境设置
问题2:.李四为什么走了?
[答案] “不该走的又走了”的等价命题是“没走的应该走”,李四觉得自己是应该走的.
问题3:.若
[答案] 正确.若
问题4:.“
[答案] “
新知生成
充要条件
(1) 如果“若 ,则 ”和“若 ,则 ”均是真命题,即既有________,又有________,就记作_________.此时, 既是 的充分条件,也是 的必要条件,我们说 是 的充分必要条件,简称为___________.
充要条件
(2) 当 是 的充要条件时, 也是 的_______条件.
充要
(3) 是 的充要条件也常常说成“ 成立___________ 成立”或“ 与 _______”.
当且仅当
等价
特别提醒:从概念的角度去理解充分条件、必要条件、充要条件
(1)若
(2)若
(3)若
(4)若
(5)若
新知运用
例3 指出下列各题中,
(1)在
(2)
(3)已知
[解析] (1)在 中,显然有 , 是 的充要条件.
(2)方程 有两个不同的实根 ,且 ,且 ,
是 的既不充分也不必要条件.
(3) , 是 的充要条件.
, 中至少有一个不为零的充要条件是( @47@ ).
A. B. C. D.
D
[解析] 若 ,则 , 不同时为零;若 , 中至少有一个不为零,则 .故选D.
巩固训练
探究3 充要条件的证明
已知关于
问题1:.由
[答案] 充分性;
情境设置
问题2:.由方程
[答案] 必要条件.
问题3:.互为充要条件是指条件和结论是相对的,在充要条件问题的证明中,条件是确定的吗?
[答案] 互为充要条件中,条件和结论是相对的,在充要条件问题的证明中,条件是确定的.
新知生成
充要条件的证明一般分为两个步骤,即分别证明“充分性”和“必要性”这两个方面.解题时要避免将充分性当作必要性来证明,这就需要分清条件与结论,若“条件”
新知运用
例4 证明:一元二次方程
方法指导 解答本题可先确定
[解析] 先证充分性: , , .
∴方程 有两个实数根.
设方程 的两个根分别为 , ,
则 ,
∴一元二次方程 有一个正实数根和一个负实数根.
再证必要性:∵一元二次方程 有一个正实数根和一个负实数根, , ,
.
故一元二次方程 有一个正实数根和一个负实数根的充要条件是 .
求证:关于
[解析] 设 方程 有一个根是1, .
①必要性:
是方程 的根,
,即 .
②充分性:
由 ,得 .
, ,
,
即 ,
是方程的一个根.
故方程 有一个根是1的充要条件是 .
巩固训练
1.若 ,则“ ”是“ ”的( @54@ ).
A.充分不必要条件 B.必要不充分条件
C.既不充分也不必要条件 D.充要条件
A
[解析] 因为“ ” “ ”,而“ ” “ ”,所以“ ”是“ ”的充分不必要条件,故选 .
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.“ ”是“ ”的( @56@ ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
B
[解析] ,∴“ ”是“ ”的必要不充分条件.故选B.
3.函数 的图象关于直线 对称的充要条件是__________.
[解析] 若函数 的图象关于直线 对称,则 ,即 ;反之,若 ,则函数 的图象关于直线 对称.
4.已知
[解析] 由 , ,得集合 .
由 ,得集合 .
因为 ,所以 ,
所以 解得 ,
所以实数 的取值范围是 .
第一章 集合与常用逻辑用语
1.4 充分条件与必要条件
榆次一中 数学教研组
学习目标
1.理解充分条件、必要条件、充要条件的概念.(数学抽象)
2.了解充分条件与判定定理,必要条件与性质定理,充要条件与性质定理的关系.(逻辑推理)
3.能通过充分性、必要性解决简单的问题.(逻辑推理)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
1.初中我们学过的命题的定义是什么?
[答案] 判断一件事的语句.
2.命题的常用形式是什么?
[答案] 数学中的命题常可以写成“如果……那么……”的形式.
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
3.何为真命题?何为假命题?
[答案] 如果题设成立,那么结论一定成立的命题为真命题,结论不能保证一定成立的为假命题.
4.命题“若
[答案] 充分条件.
5.命题“若
[答案] 不充分条件.
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 如果 是 的必要条件,那么 是唯一的.( )
×
(2) 是 的必要条件的含义是:如果 不成立,那么 一定不成立.( )
√
(3) “ ”是“ , 都大于0”成立的充分条件.( )
×
(4) 若 是 的充分条件,则 是 的必要条件.( )
√
自学检测
2.(多选题)下列条件中是 的充分条件的是( @10@ ).
A. B. C. D.
BCD
[解析] 当 时, ,但 ,故A错误,B,C,D都正确.
3.若 , ,则 是 的_______条件.(填“充分”“必要”或“充要”)
必要
[解析] ,即 ,故 是 的必要条件.
4.若 是 的充要条件, 是 的充要条件,则 是 的_______条件.(填“充分”“必要”或“充要”)
充要
[解析] 依题意, , ,所以 .
探究1 充分条件、必要条件
如图,这一个电路图,其中
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题1:.
[答案] 一定.
问题2:.
[答案] 不一定.
问题3:.
[答案] 充分条件.
新知生成
1.命题的概念及结构
(1) 一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫作_______.判断为真的语句是_________,判断为假的语句是_________.
命题
真命题
假命题
(2) 当命题表示为“若 ,则 ”时,____是命题的条件,____是命题的结论.
2.充分条件与必要条件
一般地,“若 ,则 ”为_________,是指由 通过推理可以得出 .这时,我们就说,由 可以推出 ,记作 ,并且说, 是 的___________, 是 的___________.
如果“若 ,则 ”为假命题,那么由条件 不能推出结论 ,记作 .此时,我们就说 不是 的___________, 不是 的___________.
真命题
充分条件
必要条件
充分条件
必要条件
特别提醒:
1.
(1)“若
(2)由条件
(3)
(4)只要有条件
(5)为得到结论
显然,
(1)所谓充分,就是说条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证的.“有之必成立,无之未必不成立”.
(2)充分条件不是唯一的,如
2.对充分条件的理解
新知运用
一、必要条件
例1 下列“若
(1)若一个四边形是等腰梯形,则这个四边形的两条对角线相等;
(2)若
(3)若
(4)若关于
[解析] (1)等腰梯形的两条对角线相等,因此 ,所以 是 的必要条件.
(2)直角三角形不一定是等腰三角形,因此 ,所以 不是 的必要条件.
(3)命题“若 ,则 ”是真命题,因此 ,所以 是 的必要条件.
(4)命题“若关于 的方程 有唯一解,则 ”为假命题,因此 ,所以 不是 的必要条件.
方法总结 必要条件的两种判断方法
(1)定义法:
(2)命题判断法:
若命题“若
二、充分条件
例2 下列“若
(1)若
(2)若
(3)若
(4)若
(5)在
(6)若四边形
[解析] (1)因为 ,所以 ,所以 是 的充分条件.
(2)因为 ,所以 .因此 ,所以 是 的充分条件.
(3)若 , ,则 ,但 ,所以 ,所以 不是 的充分条件.
(4)由 可以推出 或 ,不一定有 ,因此 ,所以 不是 的充分条件.
(5)由三角形中大角对大边可知,若 ,则 ,因此 ,所以 是 的充分条件.
(6)由菱形和正方形的定义可知,所有的正方形都是菱形,所以 ,所以 是 的充分条件.
方法总结 充分条件的两种判断方法
(1)定义法:
(2)命题判断法:
若命题“若
1.设集合 , ,则“ ”是“ ”的_______条件.(填“充分”或“必要”)
必要
[解析] 因为集合 , ,当 时, .因为“ ” “ ”,但“ ” “ ”,所以“ ”是“ ”的必要条件.
2.设集合 , ,那么“ ”是“ ”的_______条件.(填“充分”或“必要”)
充分
[解析] 由题意得 ,所以“ ” “ ”,所以“ ”是“ ”的充分条件.
巩固训练
探究2 充要条件
老张邀请张三、李四、王五三个人吃饭,时间到了,只有张三、李四准时赴约,王五因事不能到场,老张说:“该来的没有来.”张三听了脸色一沉,起来一声不吭地走了.老张愣了片刻,又道了句:“不该走的又走了.”李四听了大怒,拂袖而去.
问题1:.张三为什么走了?
[答案] “该来的没有来”的等价命题是“来了的都不该来”,张三觉得自己是不该来的.
情境设置
问题2:.李四为什么走了?
[答案] “不该走的又走了”的等价命题是“没走的应该走”,李四觉得自己是应该走的.
问题3:.若
[答案] 正确.若
问题4:.“
[答案] “
新知生成
充要条件
(1) 如果“若 ,则 ”和“若 ,则 ”均是真命题,即既有________,又有________,就记作_________.此时, 既是 的充分条件,也是 的必要条件,我们说 是 的充分必要条件,简称为___________.
充要条件
(2) 当 是 的充要条件时, 也是 的_______条件.
充要
(3) 是 的充要条件也常常说成“ 成立___________ 成立”或“ 与 _______”.
当且仅当
等价
特别提醒:从概念的角度去理解充分条件、必要条件、充要条件
(1)若
(2)若
(3)若
(4)若
(5)若
新知运用
例3 指出下列各题中,
(1)在
(2)
(3)已知
[解析] (1)在 中,显然有 , 是 的充要条件.
(2)方程 有两个不同的实根 ,且 ,且 ,
是 的既不充分也不必要条件.
(3) , 是 的充要条件.
, 中至少有一个不为零的充要条件是( @47@ ).
A. B. C. D.
D
[解析] 若 ,则 , 不同时为零;若 , 中至少有一个不为零,则 .故选D.
巩固训练
探究3 充要条件的证明
已知关于
问题1:.由
[答案] 充分性;
情境设置
问题2:.由方程
[答案] 必要条件.
问题3:.互为充要条件是指条件和结论是相对的,在充要条件问题的证明中,条件是确定的吗?
[答案] 互为充要条件中,条件和结论是相对的,在充要条件问题的证明中,条件是确定的.
新知生成
充要条件的证明一般分为两个步骤,即分别证明“充分性”和“必要性”这两个方面.解题时要避免将充分性当作必要性来证明,这就需要分清条件与结论,若“条件”
新知运用
例4 证明:一元二次方程
方法指导 解答本题可先确定
[解析] 先证充分性: , , .
∴方程 有两个实数根.
设方程 的两个根分别为 , ,
则 ,
∴一元二次方程 有一个正实数根和一个负实数根.
再证必要性:∵一元二次方程 有一个正实数根和一个负实数根, , ,
.
故一元二次方程 有一个正实数根和一个负实数根的充要条件是 .
求证:关于
[解析] 设 方程 有一个根是1, .
①必要性:
是方程 的根,
,即 .
②充分性:
由 ,得 .
, ,
,
即 ,
是方程的一个根.
故方程 有一个根是1的充要条件是 .
巩固训练
1.若 ,则“ ”是“ ”的( @54@ ).
A.充分不必要条件 B.必要不充分条件
C.既不充分也不必要条件 D.充要条件
A
[解析] 因为“ ” “ ”,而“ ” “ ”,所以“ ”是“ ”的充分不必要条件,故选 .
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.“ ”是“ ”的( @56@ ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
B
[解析] ,∴“ ”是“ ”的必要不充分条件.故选B.
3.函数 的图象关于直线 对称的充要条件是__________.
[解析] 若函数 的图象关于直线 对称,则 ,即 ;反之,若 ,则函数 的图象关于直线 对称.
4.已知
[解析] 由 , ,得集合 .
由 ,得集合 .
因为 ,所以 ,
所以 解得 ,
所以实数 的取值范围是 .
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
