2022-2023学年高一数学同步优品讲练课件(人教A版2019必修第一册)2.2 基本不等式(课时1 基本不等式的概念及其应用(一))(共32张PPT)
文档属性
| 名称 | 2022-2023学年高一数学同步优品讲练课件(人教A版2019必修第一册)2.2 基本不等式(课时1 基本不等式的概念及其应用(一))(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 22:39:13 | ||
图片预览










文档简介
(共32张PPT)
第二章 一元二次函数、方程和不等式
2.2 基本不等式
课时1 基本不等式的概念及其应用(一)
榆次一中 数学教研组
学习目标
1.掌握基本不等式及其推导过程.(逻辑推理)
2.能熟练运用基本不等式比较两个实数的大小.(数学运算)
3.能初步运用基本不等式进行证明和求最值.(数学运算)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
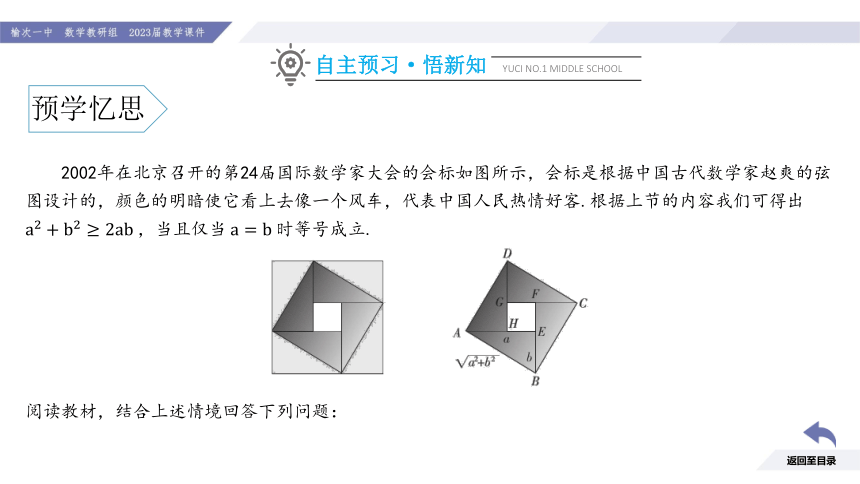
2002年在北京召开的第24届国际数学家大会的会标如图所示,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.根据上节的内容我们可得出
阅读教材,结合上述情境回答下列问题:
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
1.若以
[答案]
2.问题1的结论中,“=”何时成立?
[答案] 当且仅当
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 对于任意 , , .( )
√
(2) 当 时, .( )
√
(3) 当 时, .( )
×
(4) 若 ,则 的最小值为 .( )
×
自学检测
2.已知 ,则下列不等式正确的是( @7@ ).
A. B.
C. D.
C
[解析] 当 时, , ,故A, 错误.
当 时,由基本不等式的性质可得 , ,故C正确,D错误.
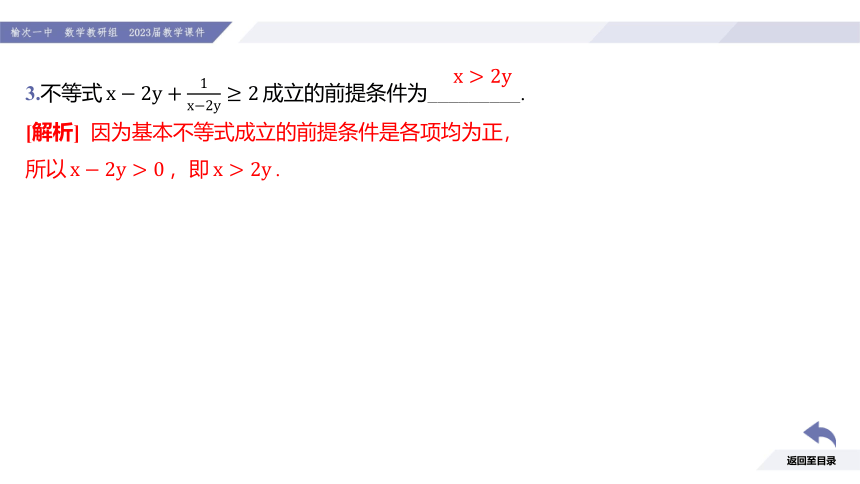
3.不等式 成立的前提条件为_________.
[解析] 因为基本不等式成立的前提条件是各项均为正,
所以 ,即 .
4.已知
[解析] , , 都是正数,
, , ,
,
,
即 ,当且仅当 时,等号成立.
探究1 基本不等式
如图,
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题1:.如何用
[答案]
问题2:.比较
[答案]
问题3:.阅读教材用分析法证明的过程,请问每一步推理的依据是什么?
[答案] 教材的证明过程的依据是②
问题4:.教材的证明方法叫作“分析法”.你能归纳一下用分析法证明命题的思路吗?
[答案] 分析法是一种“执果索因”的证明方法,即从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的充分条件(已知条件、定理、定义、公理等)为止.
问题5:.你能说说分析法的证明格式是怎样的吗?
[答案] 由于分析法是从要证明的结论出发,逐步寻求使它成立的充分条件,所以分析法在书写过程中必须有相应的文字说明.一般每一步的推理都用“要证……只要证……”的格式,当推导到一个明显成立的条件之后,指出“显然……成立”.
新知生成
1.有关概念:当
2.基本不等式:当 , 是任意正实数时, , 的几何平均数小于或等于它们的算术平均数,即 ,当且仅当________时,等号成立.
新知运用
例1 判断下列推导过程是否正确.
(1)
(2)
[解析] (1)因为 , ,当 时不符合基本不等式的使用条件,所以(1)的推导是错误的.
(2)由 ,知 , 均为负数,在推导过程中,将其转变为正数 , 后,符合基本不等式的使用条件,故(2)的推导正确.
方法总结 应用基本不等式时,注意下列常见变形中等号成立的条件:
(1)
(2)
1.在不等式 中,等号成立的条件是( @19@ ).
A. B. C. D.
C
[解析] ,∴当 ,即 时,等号成立.
巩固训练
2.已知 , ,且 ,则下列结论恒成立的是( @21@ ).
A. B. C. D.
D
[解析] 对于A,当 时, ,A错误;对于 , , 只能说明 , 同号,当 , 都小于0时, , 错误;对于D,因为 ,所以 , ,所以 ,即 恒成立,D正确.故选D.
探究2 基本不等式的简单应用
小区有一个面积为8的直角三角形花坛.
问题1:.上述情境中,能否求出两条直角边的边长之和的最小值?
[答案] 设两条直角边的边长分别为
情境设置
问题2:.若这个直角三角形的两条直角边的边长之和为4,如何求该直角三角形面积的最大值呢?
[答案] 设两条直角边的边长分别为
所以
所以该直角三角形面积的最大值为2.
新知生成
1.求最值的方法
已知
(1)如果积
(2)如果和
利用基本不等式求最值时,必须按照“一正,二定,三相等”的原则进行,即
①一正:符合基本不等式
②二定:化不等式的一边为定值.
③三相等:必须存在取“=”的条件,即“=”成立.
以上三点缺一不可.
2.基本不等式的变形
(1)
(2)
新知运用
一、利用基本不等式求最值
例2 (1)已知
(2)已知
(3)当
[解析] (1) , ,
,
当且仅当 ,即 时,等号成立,
故当 时, .
(2) , ,
,当且仅当 ,即 时,等号成立,故 .
(3) , ,当且仅当 ,即 时,等号成立,故 .
方法总结 利用基本不等式求最值的方法
利用基本不等式求最值,关键是通过恒等变形及配凑,使“和”或“积”为定值.常见的变形方法有拆、并、配.
(1)拆——裂项拆项:对分子的次数不低于分母次数的分式进行整式分离——分离成整式与“真分式”的和,再根据分式中分母的情况对整式进行拆项,为应用基本不等式凑定积创造条件;
(2)并——分组并项:目的是分组后各组可以单独应用基本不等式,或分组后先对一组应用基本不等式,再在组与组之间应用基本不等式得出最值;
(3)配——配式、配系数:有时为了挖掘出“积”或“和”为定值,常常需要根据题设条件采取合理配式、配系数的方法,使配式与待求式相乘后可以应用基本不等式得出定值,或配以恰当的系数后,使积式中的各项之和为定值.
二、利用基本不等式证明
例3 已知
[解析] 因为 , , , ,所以 ,当且仅当 时,等号成立.
所以 .
方法总结 利用基本不等式证明不等式的策略与注意事项
(1)策略:从已证不等式和问题的已知条件出发,借助不等式的性质和有关定理,经过逐步的逻辑推理,最后转化为所求问题,其特征是以“已知”看“可知”,逐步推向“未知”.
(2)注意事项:
①多次使用基本不等式时,要注意等号能否成立;
②累加法是不等式证明中的一种常用方法,证明不等式时注意使用;
③对不能直接使用基本不等式证明的可重新组合,构成基本不等式模型再使用.
(1)已知
(2)已知
[解析] (1) , 且 ,
∴由基本不等式可得 ,
当且仅当 时, 取得最大值 .
(2)
巩固训练
.
当且仅当 时,等号成立.
1.(多选题)下列说法中正确的是( @28@ ).
A. 成立的条件是 ,
B. 成立的条件是 ,
C. 成立的条件是 ,
D. 成立的条件是
BC
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.若 ,则下列不等式一定成立的是( @29@ ).
A. B.
C. D.
C
[解析] , , ,
, .
故 .
3.已知
[解析] , 为正实数,且 ,
,
当且仅当 时“=”成立.
第二章 一元二次函数、方程和不等式
2.2 基本不等式
课时1 基本不等式的概念及其应用(一)
榆次一中 数学教研组
学习目标
1.掌握基本不等式及其推导过程.(逻辑推理)
2.能熟练运用基本不等式比较两个实数的大小.(数学运算)
3.能初步运用基本不等式进行证明和求最值.(数学运算)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
2002年在北京召开的第24届国际数学家大会的会标如图所示,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.根据上节的内容我们可得出
阅读教材,结合上述情境回答下列问题:
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
1.若以
[答案]
2.问题1的结论中,“=”何时成立?
[答案] 当且仅当
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 对于任意 , , .( )
√
(2) 当 时, .( )
√
(3) 当 时, .( )
×
(4) 若 ,则 的最小值为 .( )
×
自学检测
2.已知 ,则下列不等式正确的是( @7@ ).
A. B.
C. D.
C
[解析] 当 时, , ,故A, 错误.
当 时,由基本不等式的性质可得 , ,故C正确,D错误.
3.不等式 成立的前提条件为_________.
[解析] 因为基本不等式成立的前提条件是各项均为正,
所以 ,即 .
4.已知
[解析] , , 都是正数,
, , ,
,
,
即 ,当且仅当 时,等号成立.
探究1 基本不等式
如图,
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题1:.如何用
[答案]
问题2:.比较
[答案]
问题3:.阅读教材用分析法证明的过程,请问每一步推理的依据是什么?
[答案] 教材的证明过程的依据是②
问题4:.教材的证明方法叫作“分析法”.你能归纳一下用分析法证明命题的思路吗?
[答案] 分析法是一种“执果索因”的证明方法,即从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的充分条件(已知条件、定理、定义、公理等)为止.
问题5:.你能说说分析法的证明格式是怎样的吗?
[答案] 由于分析法是从要证明的结论出发,逐步寻求使它成立的充分条件,所以分析法在书写过程中必须有相应的文字说明.一般每一步的推理都用“要证……只要证……”的格式,当推导到一个明显成立的条件之后,指出“显然……成立”.
新知生成
1.有关概念:当
2.基本不等式:当 , 是任意正实数时, , 的几何平均数小于或等于它们的算术平均数,即 ,当且仅当________时,等号成立.
新知运用
例1 判断下列推导过程是否正确.
(1)
(2)
[解析] (1)因为 , ,当 时不符合基本不等式的使用条件,所以(1)的推导是错误的.
(2)由 ,知 , 均为负数,在推导过程中,将其转变为正数 , 后,符合基本不等式的使用条件,故(2)的推导正确.
方法总结 应用基本不等式时,注意下列常见变形中等号成立的条件:
(1)
(2)
1.在不等式 中,等号成立的条件是( @19@ ).
A. B. C. D.
C
[解析] ,∴当 ,即 时,等号成立.
巩固训练
2.已知 , ,且 ,则下列结论恒成立的是( @21@ ).
A. B. C. D.
D
[解析] 对于A,当 时, ,A错误;对于 , , 只能说明 , 同号,当 , 都小于0时, , 错误;对于D,因为 ,所以 , ,所以 ,即 恒成立,D正确.故选D.
探究2 基本不等式的简单应用
小区有一个面积为8的直角三角形花坛.
问题1:.上述情境中,能否求出两条直角边的边长之和的最小值?
[答案] 设两条直角边的边长分别为
情境设置
问题2:.若这个直角三角形的两条直角边的边长之和为4,如何求该直角三角形面积的最大值呢?
[答案] 设两条直角边的边长分别为
所以
所以该直角三角形面积的最大值为2.
新知生成
1.求最值的方法
已知
(1)如果积
(2)如果和
利用基本不等式求最值时,必须按照“一正,二定,三相等”的原则进行,即
①一正:符合基本不等式
②二定:化不等式的一边为定值.
③三相等:必须存在取“=”的条件,即“=”成立.
以上三点缺一不可.
2.基本不等式的变形
(1)
(2)
新知运用
一、利用基本不等式求最值
例2 (1)已知
(2)已知
(3)当
[解析] (1) , ,
,
当且仅当 ,即 时,等号成立,
故当 时, .
(2) , ,
,当且仅当 ,即 时,等号成立,故 .
(3) , ,当且仅当 ,即 时,等号成立,故 .
方法总结 利用基本不等式求最值的方法
利用基本不等式求最值,关键是通过恒等变形及配凑,使“和”或“积”为定值.常见的变形方法有拆、并、配.
(1)拆——裂项拆项:对分子的次数不低于分母次数的分式进行整式分离——分离成整式与“真分式”的和,再根据分式中分母的情况对整式进行拆项,为应用基本不等式凑定积创造条件;
(2)并——分组并项:目的是分组后各组可以单独应用基本不等式,或分组后先对一组应用基本不等式,再在组与组之间应用基本不等式得出最值;
(3)配——配式、配系数:有时为了挖掘出“积”或“和”为定值,常常需要根据题设条件采取合理配式、配系数的方法,使配式与待求式相乘后可以应用基本不等式得出定值,或配以恰当的系数后,使积式中的各项之和为定值.
二、利用基本不等式证明
例3 已知
[解析] 因为 , , , ,所以 ,当且仅当 时,等号成立.
所以 .
方法总结 利用基本不等式证明不等式的策略与注意事项
(1)策略:从已证不等式和问题的已知条件出发,借助不等式的性质和有关定理,经过逐步的逻辑推理,最后转化为所求问题,其特征是以“已知”看“可知”,逐步推向“未知”.
(2)注意事项:
①多次使用基本不等式时,要注意等号能否成立;
②累加法是不等式证明中的一种常用方法,证明不等式时注意使用;
③对不能直接使用基本不等式证明的可重新组合,构成基本不等式模型再使用.
(1)已知
(2)已知
[解析] (1) , 且 ,
∴由基本不等式可得 ,
当且仅当 时, 取得最大值 .
(2)
巩固训练
.
当且仅当 时,等号成立.
1.(多选题)下列说法中正确的是( @28@ ).
A. 成立的条件是 ,
B. 成立的条件是 ,
C. 成立的条件是 ,
D. 成立的条件是
BC
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.若 ,则下列不等式一定成立的是( @29@ ).
A. B.
C. D.
C
[解析] , , ,
, .
故 .
3.已知
[解析] , 为正实数,且 ,
,
当且仅当 时“=”成立.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
