2022-2023学年高一数学同步优品讲练课件（人教A版2019必修第一册）3.2 函数的基本性质（课时3 函数的奇偶性）-(共34张PPT)

(共34张PPT)
第三章 函数的概念与性质
3.2 函数的基本性质
榆次一中 数学教研组
课时3 函数的奇偶性
学习目标
1.了解函数奇偶性的定义.（数学抽象）
2.掌握函数奇偶性的判断和证明方法.（逻辑推理）
3.会应用奇、偶函数图象的对称性解决简单问题.（直观想象）
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
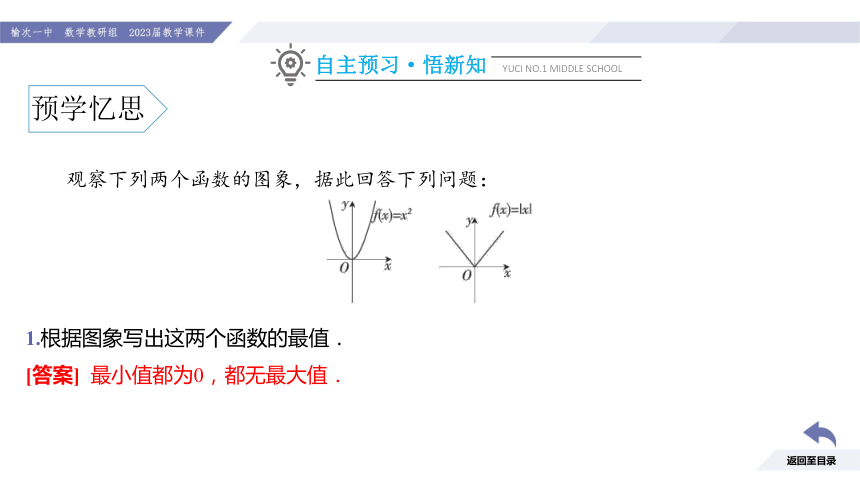
观察下列两个函数的图象，据此回答下列问题：
1.根据图象写出这两个函数的最值．
[答案] 最小值都为0，都无最大值．
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
2.这两个函数的图象有何共同特征？
[答案] 都关于 轴对称.
3.对于上述两个函数， 与 ， 与 ， 与 有什么关系？由此可得到什么一般性的结论？
[答案] ， ， .一般地，若函数 的图象关于 轴对称，当自变量 任取定义域中的一对相反数时，对应的函数值相等.即 ，满足这种性质的函数叫作偶函数.
4.怎样定义偶函数？
[答案] 如果对于函数 的定义域内任意一个 ，都有 ，那么函数 就叫作偶函数.
5.类比偶函数，考查函数 和 的类似性质，你能给出奇函数的定义吗？
[答案] 一般地，如果对于函数 的定义域内任意一个 ，都有 ，那么函数 就叫作奇函数.
1.判断下列结论是否正确.（正确的打“√”，错误的打“×”）
（1） 是定义在 上的函数，若 ，则 一定是偶函数.( )
×
（2） 对于函数 ，若存在 ，使 ，则函数 一定是奇函数.( )
×
（3） 不存在既是奇函数，又是偶函数的函数.( )
×
（4） 若函数的定义域关于原点对称，则这个函数不是奇函数就是偶函数.( )
×
自学检测
2.下列函数是偶函数的是( @10@ ).
A. B. C. D.
B
[解析] 选项A, 中的函数是奇函数，选项B中的函数是偶函数，选项D中的函数既不是奇函数，也不是偶函数．
3.下列图象表示的函数中具有奇偶性的是( @12@ ).
A. B. C. D.
B
[解析] 选项A中的图象关于原点、 轴均不对称，故排除；选项C, 中的图象所示的函数的定义域不关于原点对称，不具有奇偶性，故排除；选项B中的图象关于 轴对称，其表示的函数是偶函数.故选B.
4.若 是定义在 上的奇函数， ，则 ______， ____．

0
[解析] 因为 是定义在 上的奇函数，所以 ， ．
探究1 奇、偶函数
寿字纹是古代中国传统纹饰之一，是文字纹的一种，多施用于瓷器与布帛之上，以允装饰．
问题1：.该寿字纹图有何特点？
[答案] 既轴对称又中心对称．
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题2：.若该特点运用到函数中，函数的图象关于 轴对称，则该函数是什么函数？
[答案] 偶函数．
问题3：.若该特点运用到函数中，函数的图象关于原点中心对称，则该函数是什么函数？
[答案] 奇函数．
新知生成
1.偶函数的定义
一般地，设函数 的定义域为 ，如果_____________________________________，那么函数 就叫作偶函数．
，都有 ,且
2.偶函数的图象特征
如果一个函数是偶函数，那么这个函数的图象是以_______为对称轴的轴对称图形；反之，如果一个函数的图象关于_______对称，那么这个函数是_________．
轴
轴
偶函数
3.奇函数的定义
一般地，设函数 的定义域为 ，如果_______________________________________，那么函数 就叫作奇函数．
，都有 ,且
4.奇函数的图象特征
如果一个函数是奇函数，那么这个函数的图象是以_______为对称中心的中心对称图形；反之，如果一个函数的图象是以原点为对称中心的中心对称图形，那么这个函数是奇函数．
原点
特别提醒:（1）定义域不关于原点对称的函数，既不是奇函数也不是偶函数．
（2）对于奇函数 ，若 有意义，则 ；对于偶函数 ，必有 ．
（3）有的函数既不是奇函数，也不是偶函数，如 ；有的函数是奇函数，但不是偶函数，如 ；有的函数是偶函数，但不是奇函数，如 ；有的函数既是奇函数，又是偶函数，如 ．
新知运用
一、函数奇偶性的判断
例1 判断下列函数的奇偶性．
（1） ；（2） ；
（3） ；（4） ．
[解析] （1） 的定义域为 .
，
是奇函数．
（2） 的定义域为 . ， 是偶函数．
（3） 的定义域为 ．
∵定义域不关于原点对称， 既不是奇函数，也不是偶函数．
（4） 的定义域为 .
，
既是奇函数，又是偶函数．
方法总结 判断函数奇偶性的方法
（1）定义法：
①定义域关于原点对称；
②确定 与 的关系．
（2）图象法．
二、奇、偶函数图象的应用
例2 定义在 上的奇函数 在 上的图象如图所示．
（1）画出 的图象；
（2）解不等式 ．
[解析] （1）先描出 ， 关于原点的对称点 ， ，连线可得 的图象如图．
（2） 即图象上横坐标、纵坐标同号.结合图象可知， 的解集是 ．
【变式探究】 把本例中的“奇函数”改为“偶函数”，重做该题．
[解析] （1） 的图象如图所示，
（2） 的解集是 ．
方法总结 可以利用奇（偶）函数的图象关于原点（ 轴）对称这一特性去画图、求值、解不等式等．
1.判断下列函数的奇偶性．
（1） ；
（2） ；
（3）
巩固训练
[解析] （1）函数 的定义域为 ，不关于原点对称，所以 是非奇非偶函数．
（2） 的定义域为 ，关于原点对称．
，所以 为奇函数．
（3） 的定义域为 ，关于原点对称，
当 时， ，则 ；
当 时， ，则 ，
所以 是偶函数．
2.已知奇函数 的定义域为 ，且在区间 上的图象如图所示．
（1）画出函数 在区间 上的图象；
（2）写出使 的 的取值集合．
[解析] （1）如图，在 上的图象上选取5个关键点 ， ， ， ， ．
分别描出它们关于原点的对称点 ， ， ， ， ，再用光滑曲线连接即得．
（2）由（1）图可知，当且仅当 时， ．
∴使 的 的取值集合为 .
探究2 利用函数的奇偶性求值或参数
问题1：.若函数 是奇函数，且点 是 图象上一点，则点 是否在函数图象上？
[答案] 在．因为 为奇函数，所以 ，故点 在函数 的图象上．
情境设置
问题2：.对于定义域内的任意 ，若 ，则函数 是否具有奇偶性？若 呢？
[答案] 由 ，得 ，所以 为奇函数．
由 ，得 ，所以 为偶函数．
新知生成
1.奇（偶）函数的定义域关于_______对称．
原点
2.函数奇偶性的概念
（1） 偶函数的实质是函数 图象上任一点 关于 轴的对称点____________也在 图象上．

（2） 奇函数的实质是函数 图象上任一点 关于原点的对称点_ _____________也在 的图象上．

3.若函数 是奇函数,且在 处有定义，则必有 ，即函数图象必过原点.
新知运用
例3 （1）若函数 是偶函数，定义域为 ，则 _ ___， ____．
（2）已知函数 是奇函数，则实数 ____．

0

[解析] （1）因为偶函数的定义域关于原点对称，所以 ，解得 ．又函数 为二次函数，结合偶函数图象的特点，易得 ．
（2）由奇函数定义有 ，得 ，故 ．
方法总结 利用奇偶性求参数的常见类型
（1）定义域含参数：奇偶函数 的定义域为 ，根据定义域关于原点对称，利用 求参数．
（2）式含参数：根据 或 列式，利用待定系数法求解．
1.若函数 为偶函数，则实数 ____．
0
[解析] （法一）显然 ，
由已知得 ．
又 为偶函数，所以 ，即 ，即 .
又 ，所以 ．
（法二）由题意知 ，则 ，解得 ．
巩固训练
2.已知函数 是奇函数，当 时， .若 ，则 的值为_ ___．

[解析] ， ， ．
1.函数 ( @47@ ).
A.是奇函数 B.是偶函数
C.既是奇函数又是偶函数 D.是非奇非偶函数
B
[解析] ， 为偶函数．
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.如图，给出奇函数 的部分图象，则 的值为( @49@ ).
A. B. C. D.
A
[解析] 由图知 ， ，又 为奇函数，
所以 .
3.已知函数 ．
（1）若 为偶函数，求 的值；
（2）求函数 在 上的最值．
[解析] （1） ，
，
， ， ．
（2） 的图象关于直线 对称，因此 在 时取得最小值，最小值为 ，在 时取得最大值，最大值为24.