2022-2023学年高一数学同步优品讲练课件（人教A版2019必修第一册）3.2 函数的基本性质（课时4 函数单调性和奇偶性的综合应用）(共35张PPT)

(共35张PPT)
第三章 函数的概念与性质
3.2 函数的基本性质
榆次一中 数学教研组
课时4 函数单调性和奇偶性的综合应用
学习目标
1.掌握用奇偶性求解析式的方法.（逻辑推理）
2.理解奇偶性对单调性的影响并能用以比较大小、求最值和解不等式.（数学运算）
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
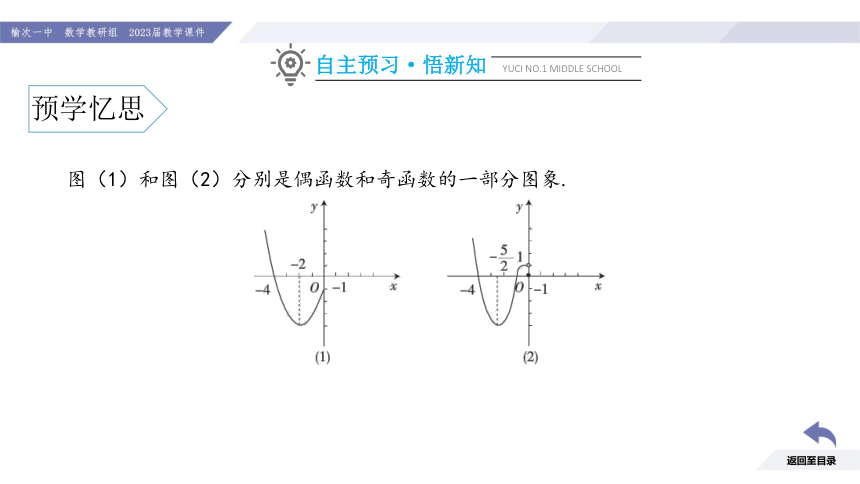
图（1）和图（2）分别是偶函数和奇函数的一部分图象.
预学忆思
自主预习·悟新知
YUCI NO.1 MIDDLE SCHOOL
1.你能结合奇偶函数图象的特征画出相应图象的另一部分吗？
[答案] 利用对称性可以画出（图略）.
2.就图（1）而言，函数在区间 与 上的单调性是否相同？就图（2）而言，函数在区间 与 上的单调性是否相同？
[答案] 不相同，相同.
1.若函数 是 上的偶函数，且在区间 上单调递增，则下列关系成立的是
( @3@ ).
A. B.
C. D.
B
[解析] ，且 在区间 上单调递增， ．
自学检测
2.若 为 上的奇函数，且在区间 上单调递减，则 _____ .（填“ ” ，“ ”或“ ”）

[解析] 为 上的奇函数，且在 上单调递减，
在 上单调递减， ．
3.如果奇函数 在区间 上单调递减，那么函数 在区间 上单调递_____.
减
[解析] 为奇函数， 在 上的单调性与在 上的一致， 在 上单调递减.
4.函数 为偶函数，若当 时， ，则 时， ______.

[解析] （法一）令 ，则 ，
，
又 为偶函数， ，
.
（法二）利用图象（图略）可得，当 时， .
探究1 利用奇偶性求函数解析式
小米给出条件“当 时， ”，再添加适当条件，求函数 的解析式.
情境设置
合作探究·提素养
YUCI NO.1 MIDDLE SCHOOL
问题1：.若添加“函数 是定义域为 的奇函数”，如何求解？
[答案] 设 ，则 ，
,
又∵函数 是定义域为 的奇函数，
，
∴当 时， .
又∵当 时， ，

问题2：.若添加“函数 是定义域为 的偶函数， ”，如何求解？
[答案] 设 ，则 ，
，
又∵函数 是定义域为 的偶函数，
，
∴当 时， .

问题3：.根据上述探究，归纳求函数解析式的方法.
[答案] “求谁设谁”，然后要利用已知区间的解析式进行代入，利用奇偶性求 .
新知生成
利用函数奇偶性求解析式的方法
（1）“求谁设谁”，即在哪个区间上求解析式， 就应在哪个区间上设.
（2）要利用已知区间的解析式进行代入.
（3）利用 的奇偶性写出 或 ，从而解出
特别提醒:若函数f(x)的定义域内含0且为奇函数,则必有f(0)=0,但若为偶函数,未必有f(0)=0.
新知运用
一、定义法求函数解析式
例1 已知 为 上的奇函数，当 时， .
（1）求 ；
（2）求 的解析式.
[解析] （1）因为函数 为奇函数，
所以 .
（2）当 时， ，则 .
由于 是奇函数，则 ，
所以 .
当 时， ，
则 ，即 .
所以 的解析式为
【变式探究】 若将本例中的“奇”改为“偶”，“ ”改为“ ”，其他条件不变，求 的解析式.
[解析] 当 时， ，此时 .因为 是偶函数，所以 ，所以 的解析式为
方法总结 利用函数奇偶性求函数解析式的三个步骤
（1）“求谁设谁”，即在哪个区间上求解析式， 就设在哪个区间上；
（2）转化到已知区间上，代入已知的解析式；
（3）利用 的奇偶性写出 或 ，从而解出 .
二、方程组法求函数解析式
例2 设 是偶函数， 是奇函数，且 ，求函数 ， 的解析式.
[解析] 是偶函数， 是奇函数， ， ，
由 ， ①
用 代替 ，得 ，
， ②
（① ②） ，得 ；（① ②） ，得 .
方法总结 已知函数 ， 的组合运算与奇偶性，则把 换为 ，构造方程组求解.
1.已知 是定义在 上的奇函数，当 时， ，则在 上 的表达式是( @17@ ).
A. B. C. D.
A
[解析] 因为当 时， ，设 ，则 ，
所以 ，又因为 是定义在 上的奇函数，
所以 .
巩固训练
2.已知函数 为偶函数，且当 时， ，则当 时， _________.

[解析] 当 时， ， ，又 为偶函数， .
探究2 奇偶性与单调性的综合应用
问题1：.如果奇函数 在区间 上单调递增，那么 在 上的单调性如何？
[答案] 如果奇函数 在区间 上单调递增，那么 在 上单调递增.
问题2：.如果偶函数 在区间 上单调递减，那么 在 上的单调性如何？
[答案] 答案 如果偶函数 在区间 上单调递减，那么 在 上单调递增.
情境设置
问题3：.你能否把上述问题所得出的结论用一句话概括出来？
[答案] 奇函数在关于原点对称的区间上的单调性相同，偶函数在关于 轴对称的区间上的单调性相反.
问题4：.如果偶函数 在 上单调递增，那么 和 的大小关系如何？若 ，你能得到什么结论？
[答案] .若 ，则 .
新知生成
（1）奇函数在区间 和 上有相同的单调性；
（2）偶函数在区间 和 上有相反的单调性.
新知运用
一、比较大小
例3 设偶函数 的定义域为 ，当 时， 是增函数，则 ， ， 的大小关系是( @25@ ).
A. B.
C. D.
A
[解析] 因为函数 为 上的偶函数，所以 ， .
又当 时， 是增函数，且 ，
所以 ，故 .
方法总结 利用函数的奇偶性与单调性比较大小
（1）自变量在同一单调区间上，直接利用函数的单调性比较大小；
（2）自变量不在同一单调区间上，需利用函数的奇偶性把自变量转化到同一单调区间上，然后利用单调性比较大小.
二、解不等式
例4 若函数 是奇函数，且在 上是增函数，又 ，则 的解集是( @27@ ).
A. B.
C. D.
A
方法指导 本题考查函数单调性和奇偶性的综合应用，并且有较强的抽象性.只要抓住其对称性，分析图象的特点，画出符合条件的图象，就不难使问题得到解决.
[解析] 由题意可画出符合条件的奇函数 的图象，如图所示.
因为 ，所以 或 结合图象，可得不等式的解集为 .
方法总结 解决不等式问题时一定要充分利用已知的条件，把已知不等式转化为 或 的形式，再根据函数的奇偶性与单调性，列出不等式
（组），要注意函数定义域对参数的影响.
1.已知偶函数 在 上单调递减，则 和 的大小关系为( @30@ ).
A. B.
C. D. 和 关系不定
A
[解析] 是偶函数，且在 上单调递减， ．
巩固训练
2.定义在 上的奇函数 为增函数，偶函数 在区间 上的图象与 的图象重合，设 ，下列不等式中成立的有_________.（填序号）
① ；② ；
③ ；④ ；
⑤ ．
①③⑤
[解析] ∵奇函数 为定义在 上的增函数，且 ， ，
又 ， ， ，
∴①正确，②错误．
当 时， ， 在 上单调递增，
，∴③正确，④错误．
又 ，∴⑤正确．
3.设定义在 上的奇函数 在区间 上单调递减，若 ，求实数 的取值范围．
[解析] 因为 是奇函数且 在 上单调递减，
所以 在 上单调递减．
所以不等式 等价于 解得 ．
所以实数 的取值范围为 .
1.已知偶函数 在 上单调递增，则( @35@ ).
A. B. C. D.以上都有可能
A
[解析] 是偶函数，且在 上单调递增，
在 上单调递减， ，故选A.
随堂检测·精评价
YUCI NO.1 MIDDLE SCHOOL
2.定义在 上的偶函数 在 上是增函数，若 ，则一定可得( @37@ ).
A. B.
C. D. 或
C
[解析] 是 上的偶函数，且在 上是增函数，
∴由 可得 .
3.已知 是定义在 上的奇函数，当 时， ，则 在 上的解析式为_ _______________________．

[解析] 设 ，则 ，
.
又 是 上的奇函数，
，
，
故
4.已知 是偶函数， 是奇函数，且 ，求 ， 的表达式．
[解析] ，由 是偶函数， 是奇函数，得 ，又 ，两式联立，得 ， .