2022-2023学年高一数学同步优品讲练课件（人教A版2019必修第一册）第一章 集合与常用逻辑用语（章末小结）(共24张PPT)

(共24张PPT)
第一章 集合与常用逻辑用语
第一章章末小结
榆次一中 数学教研组
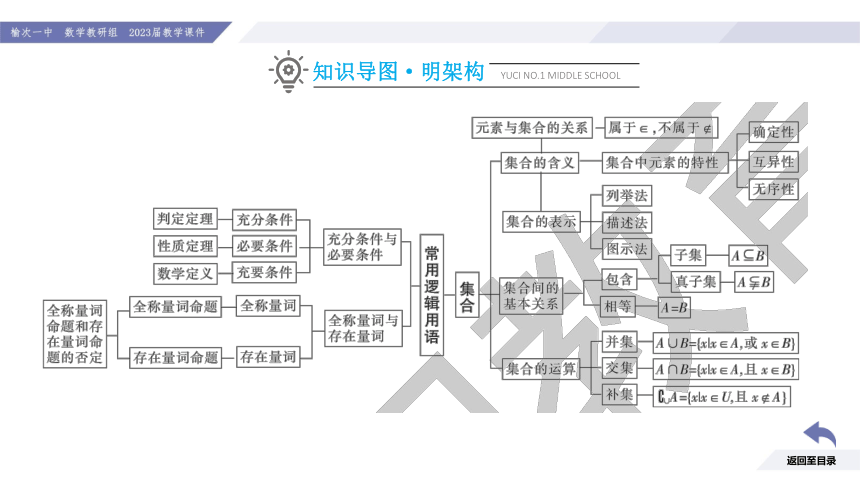
知识导图·明架构
题型探究·悟思路
拓展延伸·育素养
知识导图·明架构
YUCI NO.1 MIDDLE SCHOOL
题型1 集合间的基本关系
例1
（1） 已知集合 ， ，则下列关系正确的是( @1@ ).
A. B. C. D.
B
[解析] ，即 中的元素 ； ，即 中的元素 .故 .
题型探究·悟思路
YUCI NO.1 MIDDLE SCHOOL
（2） 已知集合 ， ，若 ，则实数 的取值范围是
( @3@ ).
A. B. C. D.
C
[解析] 由题意，在数轴上标出 ， 两个集合，如图所示，
结合数轴知，若 ，则 ，即实数 的取值范围为 ．
方法总结 借助数轴表达集合间的关系可以更直观，但操作时要规范，如区间端点的顺序、虚实不能标错.
题型2 集合的运算
例2
（1） [2021年新高考全国Ⅰ卷] 设集合 ， ，则
( @6@ ).
A. B. C. D.
B
[解析] ， ，
.故选B.
（2） [2020年全国Ⅰ卷] 设集合 ， ，且 ，则 ( @8@ ).
A. B. C. D.
B
[解析] 集合 ， ，
由 ，可得 ，则 .故选B.
（3） [2021年新高考全国Ⅱ卷] 若全集 ，集合 ， ，则 ( @10@ ).
A. B. C. D.
B
[解析] ∵全集 ，集合 ， ，
，故 .故选B.
方法总结 集合有交、并、补这三种常见的运算，它是集合中的核心内容.在进行集合的运算时，往往由于运算能力差或考虑不全面而出错，此时，数轴分析（或Venn图）是个好帮手，能将复杂问题直观化.在具体应用时要注意检验端点值是否符合题意，以免增解或漏解.
题型3 充分条件与必要条件的判定
例3
（1） 设 ，则“ ”是“ ”的( @12@ ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
B
[解析] 由 ，得 ,由 ，得 ，因为 ， ，所以“ ”是“ ”的必要不充分条件.故选B.
（2） 已知集合 ， ，则“ ”是“ ”的
( @14@ ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
A
[解析] 因为 ，而 ，且 ，所以“ ”是“ ”的充分不必要条件．
方法总结 在判定充分条件、必要条件时，要注意既要看由 能否推出 ，又要看由 能否推出 ，不能顾此失彼.
题型4 充分条件与必要条件的应用
例4 若 ， 都是实数，试从① ；② ；③ ；④ 中选出满足下列条件的式子，用序号填空：
（1）使 ， 都为0的必要条件是______________；
（2）使 ， 都不为0的充分条件是__________；
（3）使 ， 至少有一个为0的充要条件是__________．
①②③
④
①
[解析] ① 或 ，即 ， 至少有一个为0；
② ， 互为相反数，则 ， 可能均为0，也可能一个为正数一个为负数；
③ ， 为任意实数；
④ 或 即 同为正数或同为负数．
综上可知,（1）使 ， 都为0的必要条件是①②③；
（2）使 ， 都不为0的充分条件是④；
（3）使 ， 至少有一个为0的充要条件是①．
例5 已知集合 或 ．
（1）是否存在实数 ，使得 是 成立的充分条件？
（2）是否存在实数 ，使得 是 成立的必要条件？
[解析] 由 ,得 .
（1）欲使 是 成立的充分条件，
则只要 或 ，则只要 ,即 ，
故存在实数 ,使 是 成立的充分条件．
（2）欲使 是 成立的必要条件，
则只要 或 ，这是不可能的，
故不存在实数 ，使 是 成立的必要条件．
方法总结 充分条件与必要条件的应用技巧
（1）应用：可利用充分性与必要性进行相关问题的求解，特别是求参数的值或取值范围问题.
（2）求解步骤：先把 ， 等价转化，再利用充分条件、必要条件与集合间的包含关系，建立关于参数的不等式（组）进行求解.
题型5 全称量词命题与存在量词命题
例6
（1） 命题“ ， ”的否定是( @23@ ).
A. ， B. ，
C. ， D. ，
C
[解析] ∵命题“ ， ”为全称量词命题，
∴命题的否定为： ， ，故选C.
（2） 若命题 ， 是真命题，则实数 的取值范围是( @25@ ).
A. B. C. D.
B
[解析] 命题 ， 是真命题，则 ，
，
,
∴实数 的取值范围是 .故选B.
方法总结 1.全称量词命题的否定一定是存在量词命题，存在量词命题的否定一定是全称量词命题.首先改变量词，把全称量词改为存在量词，把存在量词改为全称量词，然后把判断词加以否定．
2.通过含有量词的命题的否定及利用命题的真假求参数范围等，培养逻辑推理和数学运算素养.
题型6 集合的实际应用
例7 某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26， ， ，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有____人．
8
[解析] 设参加数学、物理、化学小组的人数构成的集合分别为 ， ， ，同时参加数学和化学小组的有 人，由题意可得如图所示的Venn图．
由全班共36名同学可得 ，解得 ，即同时参加数学和化学小组的有8人．
方法总结 数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养，主要表现在：发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题，在本章主要表现在集合的实际应用问题中.
集合论的背景
集合论在19世纪诞生的基本原因来自数学基础的批判运动.数学分析的发展必然涉及无穷过程、无穷小和无穷大这些无穷概念.在18世纪，无穷概念还没有精确的定义，不仅使微积分理论遇到严重的逻辑困难，而且还使无穷概念在数学中信誉扫地.19世纪上半叶，柯西给出了极限概念的精确描述，在这基础上建立起连续、导数、微分、积分以及无穷级数的理论.正是这19世纪发展起来的极限理论解决了微积分理论所遇到的逻辑困难.但是，柯西并没有彻底完成微积分的严密化.柯西思想有一定的模糊性，甚至产生逻辑矛盾.19世纪后期的数学家们发现使柯西产生逻辑矛盾的原因在奠定微积分基础的极限概念上.严格地说,柯西的极限概念并没有真正地摆脱几何直观，确实地建立在纯粹严密的算术的基础上.于是，许多受分析基础危机影响的数学家致力于分析的严格化.在这一过程中，都涉及对微积分的基本研究对象——连续函
拓展延伸·育素养
YUCI NO.1 MIDDLE SCHOOL
数的描述.在数与连续性的定义中，有涉及关于无限的理论.因此，无限集合在数学上存在的问题又被提出来了.这也就带来寻求无限集合的理论基础的工作.
总之，寻求微积分彻底严密的算术化倾向，成了集合论产生的一个重要原因.
康托尔与集合论
康托尔是19世纪末20世纪初德国伟大的数学家，集合论的创立者.
19世纪末他所创立的集合论被誉为20世纪最伟大的数学创造，集合概
念大大扩充了数学的研究领域，给数学结构提供了一个基础，集合论
不仅影响了现代数学，而且也深深影响了现代哲学和逻辑.集合论是现
代数学中重要的基础理论.它的概念和方法已经渗透到代数、拓扑和分
析等许多数学分支以及物理学和质点力学等一些自然科学部门，为这些学科提供了奠基的方法，改变了这些学科的面貌.几乎可以说，如果没有集合论的观点，很难对现代数学获得一个深刻的理解.