人教版七年级上册3.1.1一元一次方程课件(共14张PPT)
文档属性
| 名称 | 人教版七年级上册3.1.1一元一次方程课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 07:16:02 | ||
图片预览




文档简介
(共14张PPT)
3.1 从算式到方程
第三章 一元一次方程
3.1.1 一元一次方程
你知道什么叫方程吗?
含有未知数的等式—方程
练习:
判断下列式子是不是方程,正确的打“√”,错误的打”×”:
(1) 1+2=3 ( ) (4) ( )
(2) 1+2x=4 ( ) (5) x+y=2 ( )
(3) x+1-3 ( ) (6) x2-1=0 ( )
×
×
×
√
√
√
你能举出一些方程的例子?
回顾
这样的简单方程,其中 表示未知数.
怎样根据问题中的数量关系列方程?
1
怎样解方程?
2
引例
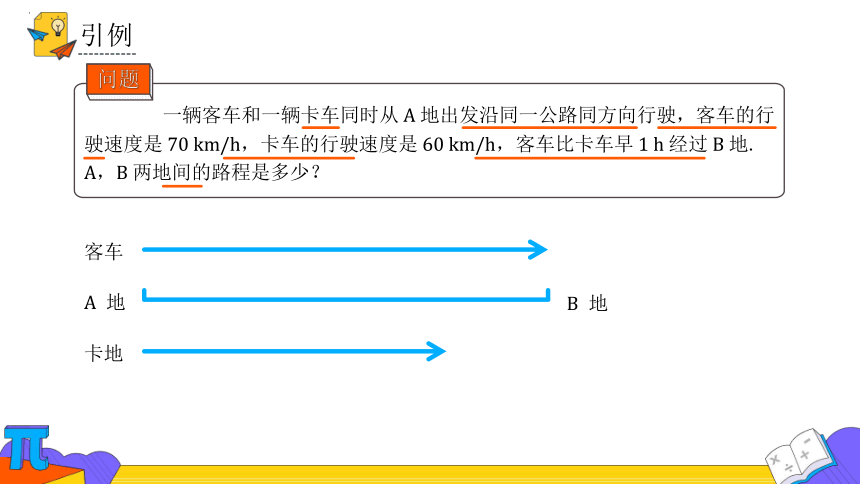
客车
地
卡地
地
一辆客车和一辆卡车同时从地出发沿同一公路同方向行驶,客车的行驶速度是,卡车的行驶速度是,客车比卡车早经过地. 两地间的路程是多少?
问题
引例
已知:速度
未知:时间,路程
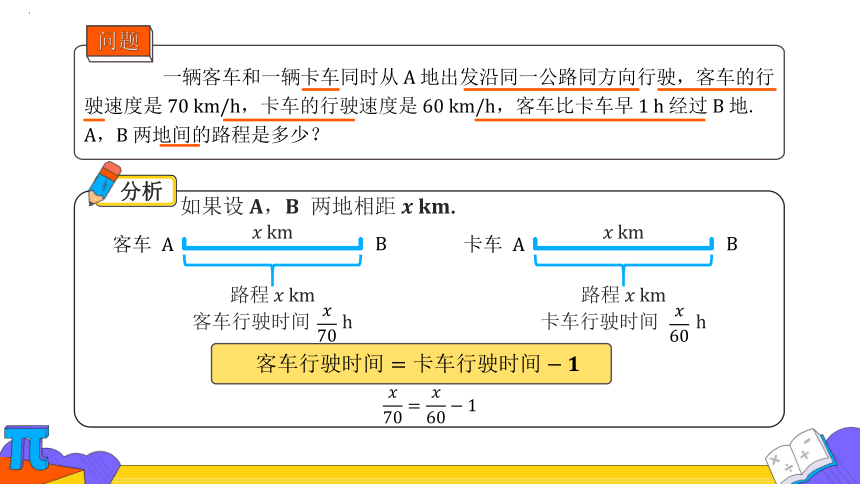
一辆客车和一辆卡车同时从地出发沿同一公路同方向行驶,客车的行驶速度是,卡车的行驶速度是,客车比卡车早经过地. 两地间的路程是多少?
问题
回顾:路程=速度×时间 速度=路程÷时间 时间=路程÷速度
分析:如果设A,B两地相距 x km,
因为客车比卡车早1 h 经过B 地,所以___ 比
____小1.
客车从A地到B地的行驶时间为______h,
卡车从A地到B地的行驶时间为_______h.
用含 x的式子表示关于时间的数量:
分析
一辆客车和一辆卡车同时从地出发沿同一公路同方向行驶,客车的行驶速度是,卡车的行驶速度是,客车比卡车早经过地. 两地间的路程是多少
问题
如果设 两地相距.
客车
行驶时间
卡车
行驶时间
思考
用算术方法和用方程解决这个问题,各有什么特点
用算术方法解题时,列出的算式只能用已知数.
用列方程法解题时,方程中既含有已知数,又含有用字母表示的未知数.
分析
小结
分析题意,圈画关键词、列表或画图找出相等关系;
1
设未知数,根据问题中的相等关系,写出含有未知数的等式——方程.
2
列方程解实际问题初始的两步:
例1 根据下列问题,设未知数并列出方程:
(1)用一根长24 cm的铁丝围成一个正方形,正方形的边
长是多少?
解:设正方形的边长为x cm,
根据题意列方程得:4x=24.
变式:用一根长24 cm的铁丝围成一个长方形,使它的长
是宽的1.5倍,长方形的长、宽各是多少?
解:设长方形的宽为x cm,则它的长为1.5x cm,
根据题意列方程得:2(x+1.5x)=24.
(2)一台计算机已使用了1 700 小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的检修时间2 450 小时?
解:设x月后这台计算机的使用时间达到2 450 小时,
那么在x月里这台计算机使用了150x 小时,
根据题意列方程得:1 700+150x=2 450.
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生数为x人,那么女生数为52%x人,
男生数为(1-52%)x人.
根据题意列方程得:52%x=(1-52%)x+80.
根据下列问题,设未知数,列出方程:
分析
单价(元支) 支数支 花费
甲种铅笔
乙种铅笔
设买甲种铅笔 支,
甲种铅笔每支 元,乙种铅笔每支 元,用 元钱买了两种铅笔共 支,两种铅笔各买了多少支
分析题意,圈画关键词、列表或画图找出相等关系;
1
设未知数,列方程.
2
列方程解实际问题初始的两步:
课
堂
小
结
3.1 从算式到方程
第三章 一元一次方程
3.1.1 一元一次方程
你知道什么叫方程吗?
含有未知数的等式—方程
练习:
判断下列式子是不是方程,正确的打“√”,错误的打”×”:
(1) 1+2=3 ( ) (4) ( )
(2) 1+2x=4 ( ) (5) x+y=2 ( )
(3) x+1-3 ( ) (6) x2-1=0 ( )
×
×
×
√
√
√
你能举出一些方程的例子?
回顾
这样的简单方程,其中 表示未知数.
怎样根据问题中的数量关系列方程?
1
怎样解方程?
2
引例
客车
地
卡地
地
一辆客车和一辆卡车同时从地出发沿同一公路同方向行驶,客车的行驶速度是,卡车的行驶速度是,客车比卡车早经过地. 两地间的路程是多少?
问题
引例
已知:速度
未知:时间,路程
一辆客车和一辆卡车同时从地出发沿同一公路同方向行驶,客车的行驶速度是,卡车的行驶速度是,客车比卡车早经过地. 两地间的路程是多少?
问题
回顾:路程=速度×时间 速度=路程÷时间 时间=路程÷速度
分析:如果设A,B两地相距 x km,
因为客车比卡车早1 h 经过B 地,所以___ 比
____小1.
客车从A地到B地的行驶时间为______h,
卡车从A地到B地的行驶时间为_______h.
用含 x的式子表示关于时间的数量:
分析
一辆客车和一辆卡车同时从地出发沿同一公路同方向行驶,客车的行驶速度是,卡车的行驶速度是,客车比卡车早经过地. 两地间的路程是多少
问题
如果设 两地相距.
客车
行驶时间
卡车
行驶时间
思考
用算术方法和用方程解决这个问题,各有什么特点
用算术方法解题时,列出的算式只能用已知数.
用列方程法解题时,方程中既含有已知数,又含有用字母表示的未知数.
分析
小结
分析题意,圈画关键词、列表或画图找出相等关系;
1
设未知数,根据问题中的相等关系,写出含有未知数的等式——方程.
2
列方程解实际问题初始的两步:
例1 根据下列问题,设未知数并列出方程:
(1)用一根长24 cm的铁丝围成一个正方形,正方形的边
长是多少?
解:设正方形的边长为x cm,
根据题意列方程得:4x=24.
变式:用一根长24 cm的铁丝围成一个长方形,使它的长
是宽的1.5倍,长方形的长、宽各是多少?
解:设长方形的宽为x cm,则它的长为1.5x cm,
根据题意列方程得:2(x+1.5x)=24.
(2)一台计算机已使用了1 700 小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的检修时间2 450 小时?
解:设x月后这台计算机的使用时间达到2 450 小时,
那么在x月里这台计算机使用了150x 小时,
根据题意列方程得:1 700+150x=2 450.
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生数为x人,那么女生数为52%x人,
男生数为(1-52%)x人.
根据题意列方程得:52%x=(1-52%)x+80.
根据下列问题,设未知数,列出方程:
分析
单价(元支) 支数支 花费
甲种铅笔
乙种铅笔
设买甲种铅笔 支,
甲种铅笔每支 元,乙种铅笔每支 元,用 元钱买了两种铅笔共 支,两种铅笔各买了多少支
分析题意,圈画关键词、列表或画图找出相等关系;
1
设未知数,列方程.
2
列方程解实际问题初始的两步:
课
堂
小
结
