人教版九年级上册22.1.4二次函数y=ax2+bx+c的图象和性质(第1课时)课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册22.1.4二次函数y=ax2+bx+c的图象和性质(第1课时)课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 588.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
22.1 二次函数的图像和性质
22.1.4 y=ax2+bx+c的图像性质
二次函数的一般式y=ax2+bx+c,有什么性质?
它的开口由什么决定?
对称轴是什么?
顶点是什么?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
用配方法解一元二次方程:x2+2x+2=0
用配方法解一元二次方程:x2+2x+2=0
y=ax2+bx+c
y=a(x-h)2+k
思考:如何将一般式化为顶点式呢?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
配方
性质
性质
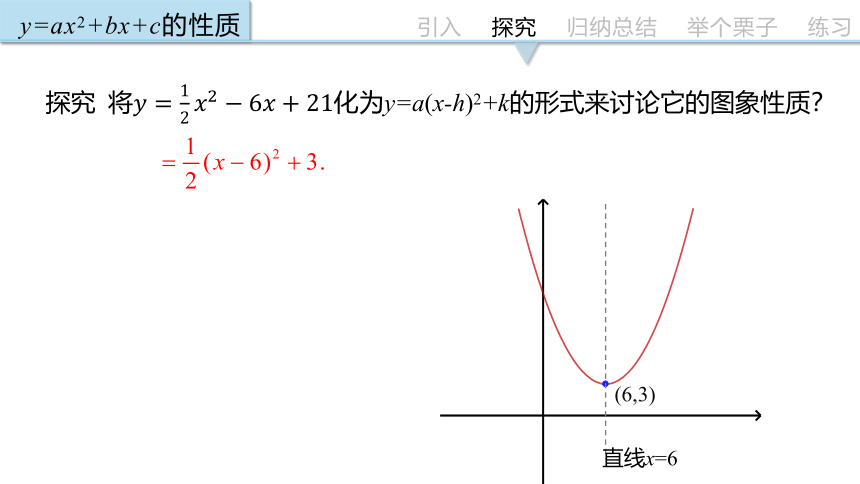
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
一般式化顶点式的步骤:
(1).提:提出二次项系数;
(2).配方:加上一次项系数一半的平方;
(3).化:化成顶点式y=a(x-h)2+k。
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
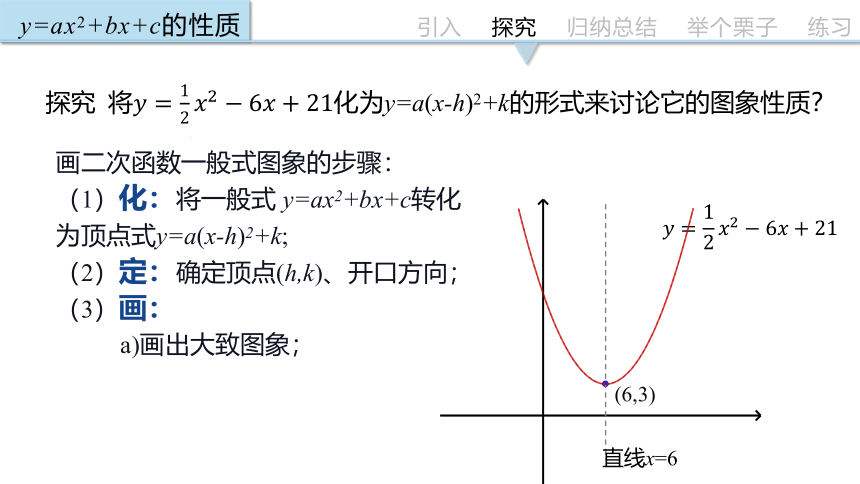
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
画二次函数一般式图象的步骤:
(1)化:将一般式 y=ax2+bx+c转化为顶点式y=a(x-h)2+k;
(2)定:确定顶点(h,k)、开口方向;
(3)画:
a)画出大致图象;
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
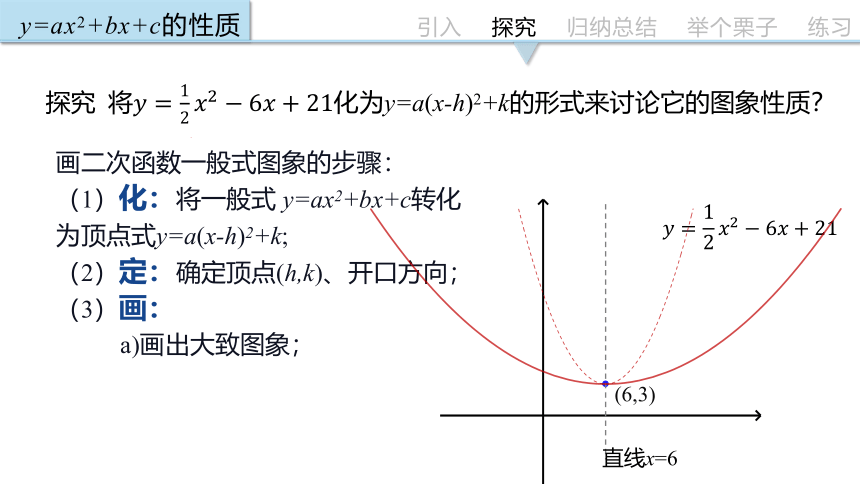
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
画二次函数一般式图象的步骤:
(1)化:将一般式 y=ax2+bx+c转化为顶点式y=a(x-h)2+k;
(2)定:确定顶点(h,k)、开口方向;
(3)画:
a)画出大致图象;
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
画二次函数一般式图象的步骤:
(1)化:将一般式 y=ax2+bx+c转化为顶点式y=a(x-h)2+k;
(2)定:确定顶点(h,k)、开口方向;
(3)画:
a)画出大致图象;
b)在对称轴两边取点,按列表、描点、连线作出准确图象。
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
小试牛刀
画出函数 的图象,并说明这个函数具有哪些性质.
(1,-2)
直线x=1
解: 函数 通过配方可得 ,
开口方向:向下
顶点坐标:(1,-2)
对称轴:x=1
增减性:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
最值:x=1时,y最大值= -2
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究将化为y=a(x-h)2+k的形式来讨论它的图象性质
一般式化顶点式的步骤:
(1).提:提出二次项系数;
(2).配方:加上一次项系数
一半的平方;
(3).化:化成顶点式
y=a(x-h)2+k。
a
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y=a (x-h)2 + k
对称轴是:直线 顶点坐标:( , )
小试牛刀
说出下列函数的对称轴、顶点坐标:
(
(
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y
x
y
x
向上
向下
a > 0
a < 0
a对函数图像有什么影响?
|a| 越大,开口越小
图像
开口方向
对称轴
顶点
增减性
最值
当x< 时,y随x的增大而减小
当x> 时,y随x的增大而增大
当x= 时,ymin=
当x< 时,y随x的增大而增大
当x> 时,y随x的增大而减小
当x= 时,ymax=
直线x=
(, )
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y
x
y
x
向上
向下
a > 0
a < 0
|a| 越大,开口越小
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
例1 二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4)
B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4)
D.开口向下,顶点坐标为(﹣1,﹣4)
A
对称轴 顶点坐标 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,1)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,- 6)
直线x=
填一填.
例2.
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
A. y轴 B.直线x=
C. 直线x=2 D.直线x=
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
例3.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
则该二次函数图象的对称轴为( )
D
1、根据公式确定下列二次函数图象的对称轴和顶点坐标:
直线x=3
直线x=8
直线x=1.25
直线x= 0.5
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
2、已知函数y=-2x2+x-4,当x= 时,y有最大值 .
3、已知二次函数y=x2-2x+1,那么它的图象大致为( )
B
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
22.1 二次函数的图像和性质
22.1.4 y=ax2+bx+c的图像性质
二次函数的一般式y=ax2+bx+c,有什么性质?
它的开口由什么决定?
对称轴是什么?
顶点是什么?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
用配方法解一元二次方程:x2+2x+2=0
用配方法解一元二次方程:x2+2x+2=0
y=ax2+bx+c
y=a(x-h)2+k
思考:如何将一般式化为顶点式呢?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
配方
性质
性质
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
一般式化顶点式的步骤:
(1).提:提出二次项系数;
(2).配方:加上一次项系数一半的平方;
(3).化:化成顶点式y=a(x-h)2+k。
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
画二次函数一般式图象的步骤:
(1)化:将一般式 y=ax2+bx+c转化为顶点式y=a(x-h)2+k;
(2)定:确定顶点(h,k)、开口方向;
(3)画:
a)画出大致图象;
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
画二次函数一般式图象的步骤:
(1)化:将一般式 y=ax2+bx+c转化为顶点式y=a(x-h)2+k;
(2)定:确定顶点(h,k)、开口方向;
(3)画:
a)画出大致图象;
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究 将化为y=a(x-h)2+k的形式来讨论它的图象性质?
(6,3)
直线x=6
画二次函数一般式图象的步骤:
(1)化:将一般式 y=ax2+bx+c转化为顶点式y=a(x-h)2+k;
(2)定:确定顶点(h,k)、开口方向;
(3)画:
a)画出大致图象;
b)在对称轴两边取点,按列表、描点、连线作出准确图象。
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
小试牛刀
画出函数 的图象,并说明这个函数具有哪些性质.
(1,-2)
直线x=1
解: 函数 通过配方可得 ,
开口方向:向下
顶点坐标:(1,-2)
对称轴:x=1
增减性:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减小;
最值:x=1时,y最大值= -2
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
探究将化为y=a(x-h)2+k的形式来讨论它的图象性质
一般式化顶点式的步骤:
(1).提:提出二次项系数;
(2).配方:加上一次项系数
一半的平方;
(3).化:化成顶点式
y=a(x-h)2+k。
a
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y=a (x-h)2 + k
对称轴是:直线 顶点坐标:( , )
小试牛刀
说出下列函数的对称轴、顶点坐标:
(
(
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y
x
y
x
向上
向下
a > 0
a < 0
a对函数图像有什么影响?
|a| 越大,开口越小
图像
开口方向
对称轴
顶点
增减性
最值
当x< 时,y随x的增大而减小
当x> 时,y随x的增大而增大
当x= 时,ymin=
当x< 时,y随x的增大而增大
当x> 时,y随x的增大而减小
当x= 时,ymax=
直线x=
(, )
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
y
x
y
x
向上
向下
a > 0
a < 0
|a| 越大,开口越小
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
例1 二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4)
B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4)
D.开口向下,顶点坐标为(﹣1,﹣4)
A
对称轴 顶点坐标 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
(1,1)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
( ,- 6)
直线x=
填一填.
例2.
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
A. y轴 B.直线x=
C. 直线x=2 D.直线x=
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
例3.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
则该二次函数图象的对称轴为( )
D
1、根据公式确定下列二次函数图象的对称轴和顶点坐标:
直线x=3
直线x=8
直线x=1.25
直线x= 0.5
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
2、已知函数y=-2x2+x-4,当x= 时,y有最大值 .
3、已知二次函数y=x2-2x+1,那么它的图象大致为( )
B
y=ax2+bx+c的性质
引入 探究 归纳总结 举个栗子 练习
同课章节目录
