广东省梅州市东海中学2022—2023学年八年级上学期开学考试数学试卷(含答案)
文档属性
| 名称 | 广东省梅州市东海中学2022—2023学年八年级上学期开学考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 288.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 17:49:36 | ||
图片预览




文档简介
2022-2023学年度第一学期丰顺县东海中学入学测验
数 学
本试卷共6页,25小题,满分120分。考试用时120分钟。
注意事项:
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名、考
号和座位号填写在答题卡上。用2B铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号。将条形码粘贴在答题卡“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
一、选择题(共10题,共30分)
(3分) 的倒数是
A. B. C. D.
(3分)已知 ,,,,,,,,请你推测 的个位数字是
A. B. C. D.
(3分)在数 ,,, 中,任取三个不同数相加,其中和最大的是
A. B. C. D.
(3分)数轴上有 ,,, 四点,各点位置与各点所表示的数如图所示.若数轴上有一点 , 点所表示的数为 ,且 ,则关于 点的位置,下列叙述正确的是
A.在 的左边 B.介于 , 之间
C.介于 , 之间 D.介于 , 之间
(3分)已知 ,若 ,则
A. B. 或
C. D. 或
(3分)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出 元,还多 元;每人出 元,还差 元,问共有多少人?这个物品的价格是多少?设这个物品的价格是 元,则可列方程为
A. B.
C. D.
(3分)有一玻璃密封器皿如图①,测得其底面直径为 厘米,高 厘米,现内装蓝色溶液若干.若如图②放置时,测得液面高 厘米;若如图③放置时,测得液面高 厘米.则该玻璃密封器皿的总容量为(结果保留 )
A. 立方厘米 B. 立方厘米
C. 立方厘米 D. 立方厘米
(3分)一个池塘的水浮莲,每天都在生长,且每天的面积是前一天的 倍.如果生长 天刚好能把整个池塘遮满,那么水浮莲长到遮住半个池塘需要
A. 天 B. 天 C. 天 D. 天
(3分)若 ,则我们把 称为 的“哈利数”,如 的“哈利数”是 , 的“哈利数”是 ,已知 , 是 的“哈利数”, 是 的“哈利数”, 是 的“哈利数”,,依此类推,则
A. B. C. D.
(3分)如图, 是一块半径为 的半圆形纸板,在 的右上端剪去一个直径为 的半圆后得到图形 ,然后依次剪去一个更小的半圆(其直径为前一个被剪去的半圆的半径)得到图形 ,,记纸板 的面积为 ,则 的值为
A. B. C. D.
二、填空题(共7题,共28分)
(4分)已知方程 是关于 的一元一次方程,则 .
(4分)已知 ,则代数式 的值是 .
(4分)已知 ,.若 的值与 的取值无关,则 的值为 .
(4分)某校购新书 本,共付 元,其中科技书每本 元,文艺书每本 元,则科技书买了 本,文艺书买了 本.
(4分)对于有理数 ,,规定一种运算:,如 ,则计算 .
(4分)我们规定:若关于 的一元一次方程 的解为 ,则称该方程为“和解方程”.例如:方程 的解为 ,而 ,则方程 为“和解方程”.请根据上述规定解答下列问题:
()已知关于 的一元一次方程 是“和解方程”,则 的值为 .
()已知关于 的一元一次方程 是“和解方程”,并且它的解是 ,则 的值为 .
(4分)观察下列等式:
第 个等式:;
第 个等式:;
第 个等式:;
第 个等式:.
请解答下列问题:
()按以上规律列出第 个等式: .
()用含有 的代数式表示第 个等式: ( 为正整数).
三、解答题(共8题,共62分)
(6分)某国际化学校实行小班制教学,七年级四个班共有学生 人,一班有学生 人,二班人数比一班人数的两倍少 人,三班人数比二班人数的一半多 人.
(1) 求三班的学生人数(用含 , 的式子表示).
(2) 求四班的学生人数(用含 , 的式子表示).
(3) 若四个班共有学生 人,求二班比三班多的学生人数?
(6分)解下列方程:
(1) .
(2) .
(7分)分别用 ,,, 表示有理数, 是最小的正整数, 是最大的负整数, 是绝对值最小的有理数, 是数轴上到原点距离为 的点表示的数,求 的倒数.
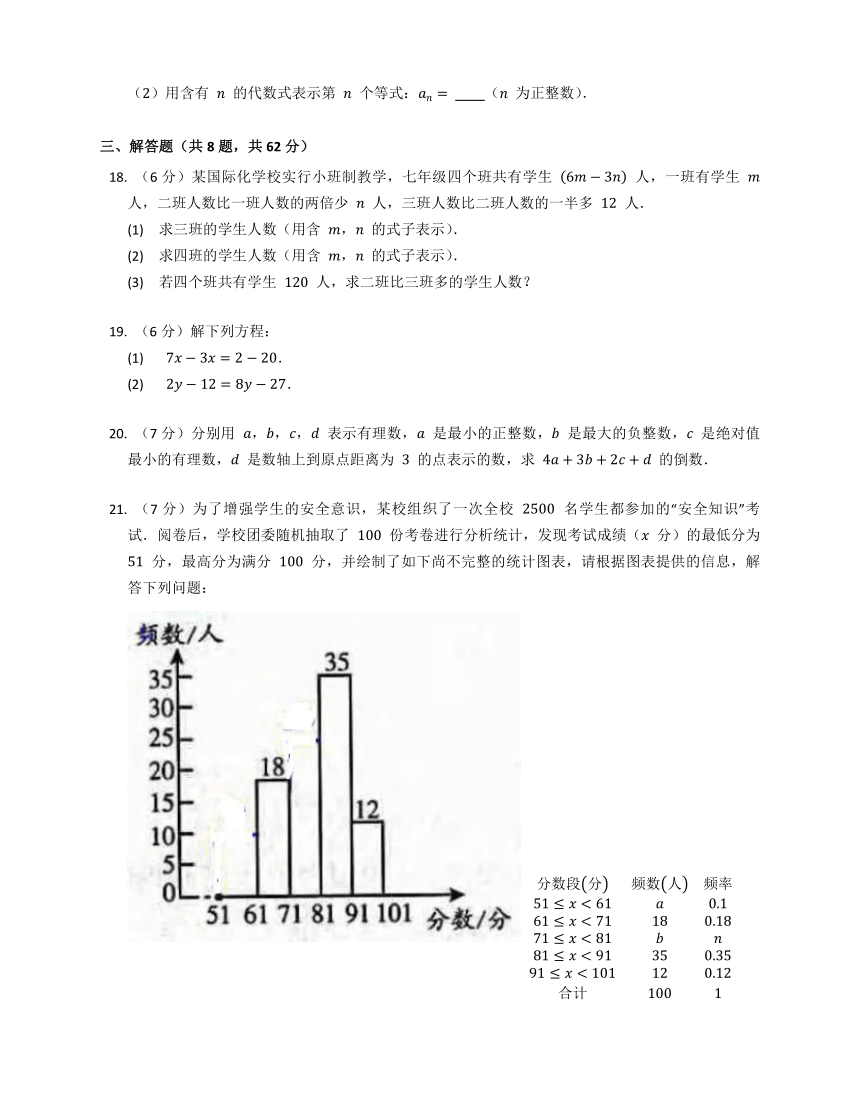
(7分)为了增强学生的安全意识,某校组织了一次全校 名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了 份考卷进行分析统计,发现考试成绩( 分)的最低分为 分,最高分为满分 分,并绘制了如下尚不完整的统计图表,请根据图表提供的信息,解答下列问题:
(1) 填空: , , .
(2) 将频数分布直方图补充完整.
(3) 该校对考试成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数.
(8分)某校七年级共有 名学生,团委准备调查他们对“低碳”知识的了解程度.
(1) 在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是 .
(2) 团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①②所示),请你根据图中信息,将其补充完整;
(3) 请你估计该校七年级约有多少名学生比较了解“低碳”知识.
(8分)计算题.
(1) .
(2) .
(3) .
(10分)已知 的值与 无关,数轴上两点 , 对应的数分别为 ,.
(1) 求 , 的值.
(2) 数轴上是否存在点 ,使点 到点 、点 的距离之和为 ?若存在,请求出其对应的数 的值,若不存在,请说明理由.
(3) 当点 以每秒 个单位长度的速度向左运动,点 以每秒 个单位长度也向左运动,若点 , 同时出发,并在点 相遇,求点 对应的数.
(4) 若点 , 保持原来速度从原来的位置相向运动,设运动时间为 秒.则当 时,求 的值.
(10分)如图,数轴上线段 (单位长度),(单位长度),点 在数轴上表示的数是 ,点 在数轴上表示的数是 .若线段 以 个单位长度/秒的速度向右匀速运动,同时线段 以 个单位长度/秒的速度向左匀速运动.
(1) 问运动时间为多少时 (单位长度)?
(2) 当运动到 (单位长度)时,点 在数轴上表示的数是 .
(3) 是线段 上一点,当 点运动到线段 上时,是否存在关系式 .若存在,求线段 的长;若不存在,请说明理由.
方法一:设运动时间为 秒,分段讨论点 的位置,通过取特殊值法反证关系式的存在,从而得到 的长.
方法二:设线段 未运动时点 所表示的数为 ,点 运动时间为 ,用含 , 的式子分别表示出线段 ,,,分情况讨论点 的位置,通过计算求得 的长.
答案
一、选择题(共10题,共30分)
1. 【答案】A
2. 【答案】B
3. 【答案】D
4. 【答案】D
5. 【答案】D
6. 【答案】D
7. 【答案】D
8. 【答案】D
9. 【答案】D
10. 【答案】C
二、填空题(共7题,共28分)
11. 【答案】
12. 【答案】
13. 【答案】
14. 【答案】 ;
15. 【答案】
16. 【答案】 ;
17. 【答案】 ;
三、解答题(共8题,共62分)
18. 【答案】
(1) 一班人数为: 人;
二班人数为: 人;
三班人数为: 人.
(2) 四班人数为:
(3) 由题意可得:,则 ,
故 二班比三班多的学生数为:
答:二班比三班多 人.
19. 【答案】
(1) 合并得:解得:
(2) 移项合并得:解得:
20. 【答案】 最小的正整数是 ,最大的负整数是 ,绝对值最小的有理数是 ,数轴上到原点距离为 的点表示的数是 ,
,,,.
当 时,
的倒数是 ;
当 时,
的倒数是 .
21. 【答案】
(1) ;;
(2)
(3)
答:全校获得二等奖的学生人数 人.
22. 【答案】
(1) 方案三
(2) 补图如图所示.
(3) (名).
23. 【答案】
(1) .
(2)
(3)
24. 【答案】
(1)
多项式的值与 无关,
,,
,.
(2) 若点 在 之间,
则有符合题意,舍去,
若点 在点 左侧,设点 表示的数为 ,则解得:若点 在点 右侧,则解得:综上所述,存在点 ,其对应的数 的值为 或 .
(3) 设 秒后,, 两相遇,根据题意可得:解得: 点 对应的数为
(4) 根据题意可得,当 时,
解得当 时,
解得综上所述, 的值为 或 .
25. 【答案】
(1) 由题意可知点 表示的数是 ,点 表示的数是 .
设运动 秒时,(单位长度),
①当点 在点 的左边时,
由题意得 ,解得 ;
②当点 在点 的右边时,
由题意得 ,解得 ;
所以当运动时间为 秒或 秒时,(单位长度).
(2) 或
(3) 存在关系式 .
方法一:
①当 时,点 和点 重合,点 在线段 上,,且 ,,
当 时,,即 ;
②当 时,点 在点 和点 之间,.
()点 在线段 上时,,,
当 时,,即 ;
()点 在线段 上时,,,
当 时,,即 ;
③当 时,点 与点 重合,,,,
当 时,,即 ;
④当 时,线段 在线段 上,,,,
当 时,,即 .
综上所述,当点 在点 左侧时,;
当点 在点 右侧时,.
所以 的长为 或 .
方法二:
设线段 未运动时点 所表示的数为 ,点 运动时间为 ,
则此时点 表示的数为 ,点 表示的数为 ,点 表示的数为 ,点 表示的数为 ,点 表示的数为 ,
所以 ,,,,
因为 ,
所以 ,
所以 ,
即 ,
①当点 在点 右侧时,
,
所以 ,
所以 ;
②当点 在点 左侧时,
,
所以 ,
所以 ;
所以 的长为 或 .
数 学
本试卷共6页,25小题,满分120分。考试用时120分钟。
注意事项:
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名、考
号和座位号填写在答题卡上。用2B铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号。将条形码粘贴在答题卡“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
一、选择题(共10题,共30分)
(3分) 的倒数是
A. B. C. D.
(3分)已知 ,,,,,,,,请你推测 的个位数字是
A. B. C. D.
(3分)在数 ,,, 中,任取三个不同数相加,其中和最大的是
A. B. C. D.
(3分)数轴上有 ,,, 四点,各点位置与各点所表示的数如图所示.若数轴上有一点 , 点所表示的数为 ,且 ,则关于 点的位置,下列叙述正确的是
A.在 的左边 B.介于 , 之间
C.介于 , 之间 D.介于 , 之间
(3分)已知 ,若 ,则
A. B. 或
C. D. 或
(3分)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出 元,还多 元;每人出 元,还差 元,问共有多少人?这个物品的价格是多少?设这个物品的价格是 元,则可列方程为
A. B.
C. D.
(3分)有一玻璃密封器皿如图①,测得其底面直径为 厘米,高 厘米,现内装蓝色溶液若干.若如图②放置时,测得液面高 厘米;若如图③放置时,测得液面高 厘米.则该玻璃密封器皿的总容量为(结果保留 )
A. 立方厘米 B. 立方厘米
C. 立方厘米 D. 立方厘米
(3分)一个池塘的水浮莲,每天都在生长,且每天的面积是前一天的 倍.如果生长 天刚好能把整个池塘遮满,那么水浮莲长到遮住半个池塘需要
A. 天 B. 天 C. 天 D. 天
(3分)若 ,则我们把 称为 的“哈利数”,如 的“哈利数”是 , 的“哈利数”是 ,已知 , 是 的“哈利数”, 是 的“哈利数”, 是 的“哈利数”,,依此类推,则
A. B. C. D.
(3分)如图, 是一块半径为 的半圆形纸板,在 的右上端剪去一个直径为 的半圆后得到图形 ,然后依次剪去一个更小的半圆(其直径为前一个被剪去的半圆的半径)得到图形 ,,记纸板 的面积为 ,则 的值为
A. B. C. D.
二、填空题(共7题,共28分)
(4分)已知方程 是关于 的一元一次方程,则 .
(4分)已知 ,则代数式 的值是 .
(4分)已知 ,.若 的值与 的取值无关,则 的值为 .
(4分)某校购新书 本,共付 元,其中科技书每本 元,文艺书每本 元,则科技书买了 本,文艺书买了 本.
(4分)对于有理数 ,,规定一种运算:,如 ,则计算 .
(4分)我们规定:若关于 的一元一次方程 的解为 ,则称该方程为“和解方程”.例如:方程 的解为 ,而 ,则方程 为“和解方程”.请根据上述规定解答下列问题:
()已知关于 的一元一次方程 是“和解方程”,则 的值为 .
()已知关于 的一元一次方程 是“和解方程”,并且它的解是 ,则 的值为 .
(4分)观察下列等式:
第 个等式:;
第 个等式:;
第 个等式:;
第 个等式:.
请解答下列问题:
()按以上规律列出第 个等式: .
()用含有 的代数式表示第 个等式: ( 为正整数).
三、解答题(共8题,共62分)
(6分)某国际化学校实行小班制教学,七年级四个班共有学生 人,一班有学生 人,二班人数比一班人数的两倍少 人,三班人数比二班人数的一半多 人.
(1) 求三班的学生人数(用含 , 的式子表示).
(2) 求四班的学生人数(用含 , 的式子表示).
(3) 若四个班共有学生 人,求二班比三班多的学生人数?
(6分)解下列方程:
(1) .
(2) .
(7分)分别用 ,,, 表示有理数, 是最小的正整数, 是最大的负整数, 是绝对值最小的有理数, 是数轴上到原点距离为 的点表示的数,求 的倒数.
(7分)为了增强学生的安全意识,某校组织了一次全校 名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了 份考卷进行分析统计,发现考试成绩( 分)的最低分为 分,最高分为满分 分,并绘制了如下尚不完整的统计图表,请根据图表提供的信息,解答下列问题:
(1) 填空: , , .
(2) 将频数分布直方图补充完整.
(3) 该校对考试成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数.
(8分)某校七年级共有 名学生,团委准备调查他们对“低碳”知识的了解程度.
(1) 在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是 .
(2) 团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①②所示),请你根据图中信息,将其补充完整;
(3) 请你估计该校七年级约有多少名学生比较了解“低碳”知识.
(8分)计算题.
(1) .
(2) .
(3) .
(10分)已知 的值与 无关,数轴上两点 , 对应的数分别为 ,.
(1) 求 , 的值.
(2) 数轴上是否存在点 ,使点 到点 、点 的距离之和为 ?若存在,请求出其对应的数 的值,若不存在,请说明理由.
(3) 当点 以每秒 个单位长度的速度向左运动,点 以每秒 个单位长度也向左运动,若点 , 同时出发,并在点 相遇,求点 对应的数.
(4) 若点 , 保持原来速度从原来的位置相向运动,设运动时间为 秒.则当 时,求 的值.
(10分)如图,数轴上线段 (单位长度),(单位长度),点 在数轴上表示的数是 ,点 在数轴上表示的数是 .若线段 以 个单位长度/秒的速度向右匀速运动,同时线段 以 个单位长度/秒的速度向左匀速运动.
(1) 问运动时间为多少时 (单位长度)?
(2) 当运动到 (单位长度)时,点 在数轴上表示的数是 .
(3) 是线段 上一点,当 点运动到线段 上时,是否存在关系式 .若存在,求线段 的长;若不存在,请说明理由.
方法一:设运动时间为 秒,分段讨论点 的位置,通过取特殊值法反证关系式的存在,从而得到 的长.
方法二:设线段 未运动时点 所表示的数为 ,点 运动时间为 ,用含 , 的式子分别表示出线段 ,,,分情况讨论点 的位置,通过计算求得 的长.
答案
一、选择题(共10题,共30分)
1. 【答案】A
2. 【答案】B
3. 【答案】D
4. 【答案】D
5. 【答案】D
6. 【答案】D
7. 【答案】D
8. 【答案】D
9. 【答案】D
10. 【答案】C
二、填空题(共7题,共28分)
11. 【答案】
12. 【答案】
13. 【答案】
14. 【答案】 ;
15. 【答案】
16. 【答案】 ;
17. 【答案】 ;
三、解答题(共8题,共62分)
18. 【答案】
(1) 一班人数为: 人;
二班人数为: 人;
三班人数为: 人.
(2) 四班人数为:
(3) 由题意可得:,则 ,
故 二班比三班多的学生数为:
答:二班比三班多 人.
19. 【答案】
(1) 合并得:解得:
(2) 移项合并得:解得:
20. 【答案】 最小的正整数是 ,最大的负整数是 ,绝对值最小的有理数是 ,数轴上到原点距离为 的点表示的数是 ,
,,,.
当 时,
的倒数是 ;
当 时,
的倒数是 .
21. 【答案】
(1) ;;
(2)
(3)
答:全校获得二等奖的学生人数 人.
22. 【答案】
(1) 方案三
(2) 补图如图所示.
(3) (名).
23. 【答案】
(1) .
(2)
(3)
24. 【答案】
(1)
多项式的值与 无关,
,,
,.
(2) 若点 在 之间,
则有符合题意,舍去,
若点 在点 左侧,设点 表示的数为 ,则解得:若点 在点 右侧,则解得:综上所述,存在点 ,其对应的数 的值为 或 .
(3) 设 秒后,, 两相遇,根据题意可得:解得: 点 对应的数为
(4) 根据题意可得,当 时,
解得当 时,
解得综上所述, 的值为 或 .
25. 【答案】
(1) 由题意可知点 表示的数是 ,点 表示的数是 .
设运动 秒时,(单位长度),
①当点 在点 的左边时,
由题意得 ,解得 ;
②当点 在点 的右边时,
由题意得 ,解得 ;
所以当运动时间为 秒或 秒时,(单位长度).
(2) 或
(3) 存在关系式 .
方法一:
①当 时,点 和点 重合,点 在线段 上,,且 ,,
当 时,,即 ;
②当 时,点 在点 和点 之间,.
()点 在线段 上时,,,
当 时,,即 ;
()点 在线段 上时,,,
当 时,,即 ;
③当 时,点 与点 重合,,,,
当 时,,即 ;
④当 时,线段 在线段 上,,,,
当 时,,即 .
综上所述,当点 在点 左侧时,;
当点 在点 右侧时,.
所以 的长为 或 .
方法二:
设线段 未运动时点 所表示的数为 ,点 运动时间为 ,
则此时点 表示的数为 ,点 表示的数为 ,点 表示的数为 ,点 表示的数为 ,点 表示的数为 ,
所以 ,,,,
因为 ,
所以 ,
所以 ,
即 ,
①当点 在点 右侧时,
,
所以 ,
所以 ;
②当点 在点 左侧时,
,
所以 ,
所以 ;
所以 的长为 或 .
同课章节目录
