2.1.3 多项式及整式 课件(共26张PPT)
文档属性
| 名称 | 2.1.3 多项式及整式 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 09:13:36 | ||
图片预览







文档简介
(共26张PPT)
七上数学同步精品课件
人教版七年级上册
2.1.3 多项式及整式
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第二章 整式的加减
1.理解多项式、整式的概念.(重点)
2.会确定一个多项式的项数和次数.(难点)
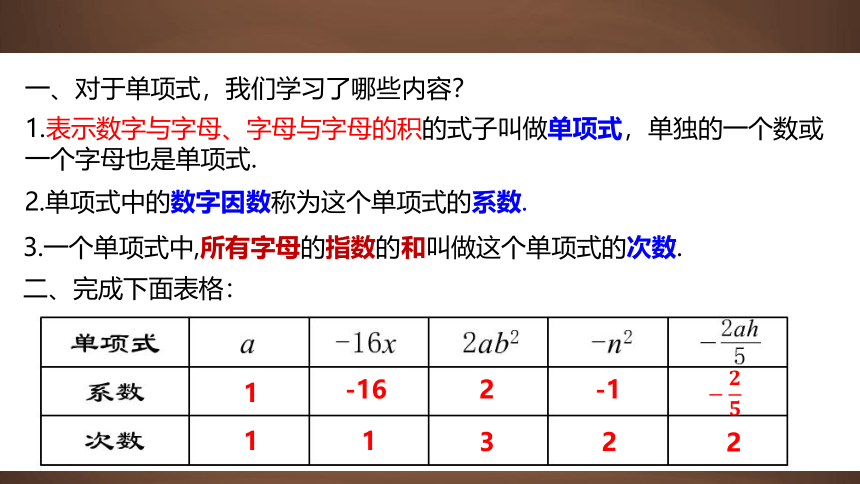
一、对于单项式,我们学习了哪些内容?
二、完成下面表格:
1.表示数字与字母、字母与字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式中的数字因数称为这个单项式的系数.
3.一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1
1
-16
1
2
3
-1
2
2
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
(t-5)
列式表示下列数量
3.如图三角尺的面积为 .
列式表示下列数量
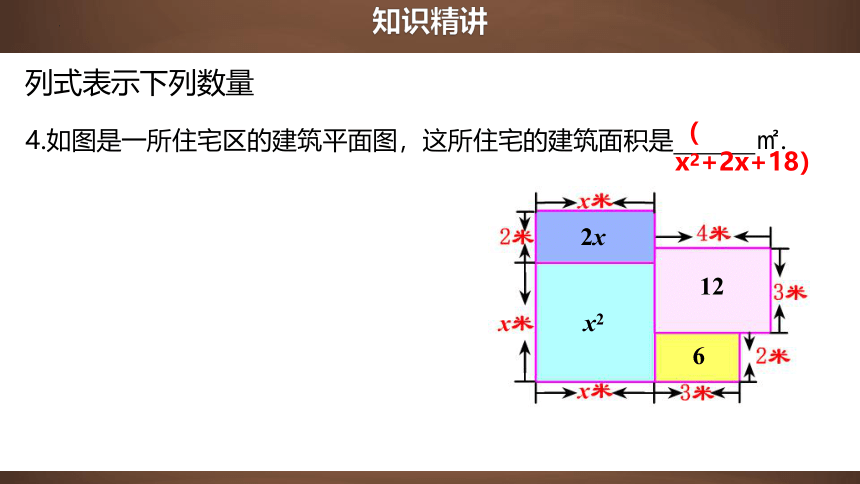
4.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
2x
12
x2
6
3x+5y+2z
x2+2x+18
t-5
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
多项式定义:
像这样,几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
例如,多项式t-5的项是t与-5,其中-5是常数项;多项式x2+2x+18的项是x2,2x和18,其中18是常数项.
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
多项式的次数:
多项式里,次数最高项的次数,叫做这个多项式的次数.
例如,多项式t-5中次数最高的项是一次项t,这个多项式的次数是1;多项式x2+2x+18中次数最高的项是二次项x2,这个多项式的次数是2.
思考:3x+5y+2z, ab-πr2的项分别是什么?次数分别是多少?
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
整式的定义
单项式与多项式统称整式.
例如,前面见到的单项式100t,0.8p,mn,a2h,-n,以及多项式t-5,3x+5y+2z,ab-πr2,x2+2x+18等都是整式.
例1.下列整式中哪些是单项式 哪些是多项式 是单项式的指出系数和次数,是多项式的指出项和次数.
-
3
6
1
1
32
3
0
例1.下列整式中哪些是单项式 哪些是多项式 是单项式的指出系数和次数,是多项式的指出项和次数.
x2,y2,-1
2
3x2,-y,3xy3,x4,-1
4
2x,-y
1
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
下列多项式有几项 分别是什么 每项的系数和次数分别是多少 最高次是几次 属于几次几项式?
(1) -2a-ab2+π (2) a4-3a3b2+2b2+52
解: (1) -2a-ab2+π有三项,分别是-2a、-ab2、兀,系数分别是-2、-1、π,次数分别是1,3,0,最高次是3次,属于三次三项式;
(2) a4-3a3b2+2b2+52有四项, 分别是a4、-3c3b2、2b2、52,系数分别是1、-3、2、52,次数分别是4、5、2、0,最高次是5次,属于五次四项式.
例2.已知关于x,y的多项式x2ym+1+xy2–2x3–5是六次四项式,单项式3x2ny5–m的次数与这个多项式的次数相同,求m-n的值.
解:因为多项式x2ym+1+xy2-2x3-5是六次四项式,
所以2+m+1=6,
所以m=3,
因为单项式6x2ny5–m的次数也是六次,
所以2n+5-m=6,
所以n=2,
所以m-n=3-2=1.
已知多项式是六次四项式,且的次数跟它相同.
(1)求m、n的值;
解:(1)因为多项式是六次四项式,
所以,
解得,,
5-m=5-3=2,
的次数与多项式的次数相同,
,解得,.
已知多项式是六次四项式,且的次数跟它相同.
(2)求多项式各项的系数和.
解:(2)各项的系数之和为:.
例3.如图,用式子表示圆环的面积.当R=15cm,r=10cm时,求圆环的面积(π取3.14).
解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是 .
当R=15cm,r=10cm时,圆环的面积(单位:cm2)是
这个圆环的面积是392.5cm2.
一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长L;
(2)花坛的面积S.
解:(1) L=2a+2πr
(2) 花坛的面积是一个长方形的面积与两个半圆的面积 之和,即S=2ar+ πr2
a
r
r
1.下列代数式,0,,,,,中,多项式的个数有( )
A.3个 B.4个 C.5个 D.6个
A
2.下列说法正确的是( )
A.单项式的系数是,次数是2 B.单项式的次数是3
C.是四次三项式 D.是二次单项式
C
4.如果一个多项式的次数是5,则这个多项式的任何一项的次数都( )
A.小于5 B.大于5 C.大于或等于5 D.小于或等于5
3.多项式的项数及次数分别是( )
A.3,2 B.3,3 C.2,3 D.3,4
D
D
5.若关于x的多项式是二次三项式,则a+b=_____.
6.关于x、y的多项式是四次二项式,则________.
7.已知关于x,y的多项式x2ym+1+xy2﹣2x3﹣5是六次四项式,单项式3x2ny5﹣m的次数与这个多项式的次数相同,则m﹣n=_____.
8.如果多项式不含和项,则______.
6
2或-3
1
-3
9.如图,文化广场上摆了一些桌子,若并排摆n张桌子,可同时容纳多少人 当n=20时,可同时容纳多少人
解: (1) 4×1+2,
(2) 4×2+2,
……
(n) 4n+2
当n=20时,4n+2=4×20+2
=82(人)
1.几个单项式的和叫做多项式;
2.在多项式中,每个单项式叫做多项式的项;
3.不含字母的项叫做常数项;
4.多项式里次数最高项的次数就是多项式的次数.
5.单项式与多项式统称为整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
七上数学同步精品课件
人教版七年级上册
2.1.3 多项式及整式
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第二章 整式的加减
1.理解多项式、整式的概念.(重点)
2.会确定一个多项式的项数和次数.(难点)
一、对于单项式,我们学习了哪些内容?
二、完成下面表格:
1.表示数字与字母、字母与字母的积的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式中的数字因数称为这个单项式的系数.
3.一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1
1
-16
1
2
3
-1
2
2
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
(t-5)
列式表示下列数量
3.如图三角尺的面积为 .
列式表示下列数量
4.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
2x
12
x2
6
3x+5y+2z
x2+2x+18
t-5
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
多项式定义:
像这样,几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
例如,多项式t-5的项是t与-5,其中-5是常数项;多项式x2+2x+18的项是x2,2x和18,其中18是常数项.
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
多项式的次数:
多项式里,次数最高项的次数,叫做这个多项式的次数.
例如,多项式t-5中次数最高的项是一次项t,这个多项式的次数是1;多项式x2+2x+18中次数最高的项是二次项x2,这个多项式的次数是2.
思考:3x+5y+2z, ab-πr2的项分别是什么?次数分别是多少?
观察式子t-5,3x+5y+2z, ab-πr2,x2+2x+18,这些式子有什么特点?
整式的定义
单项式与多项式统称整式.
例如,前面见到的单项式100t,0.8p,mn,a2h,-n,以及多项式t-5,3x+5y+2z,ab-πr2,x2+2x+18等都是整式.
例1.下列整式中哪些是单项式 哪些是多项式 是单项式的指出系数和次数,是多项式的指出项和次数.
-
3
6
1
1
32
3
0
例1.下列整式中哪些是单项式 哪些是多项式 是单项式的指出系数和次数,是多项式的指出项和次数.
x2,y2,-1
2
3x2,-y,3xy3,x4,-1
4
2x,-y
1
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
下列多项式有几项 分别是什么 每项的系数和次数分别是多少 最高次是几次 属于几次几项式?
(1) -2a-ab2+π (2) a4-3a3b2+2b2+52
解: (1) -2a-ab2+π有三项,分别是-2a、-ab2、兀,系数分别是-2、-1、π,次数分别是1,3,0,最高次是3次,属于三次三项式;
(2) a4-3a3b2+2b2+52有四项, 分别是a4、-3c3b2、2b2、52,系数分别是1、-3、2、52,次数分别是4、5、2、0,最高次是5次,属于五次四项式.
例2.已知关于x,y的多项式x2ym+1+xy2–2x3–5是六次四项式,单项式3x2ny5–m的次数与这个多项式的次数相同,求m-n的值.
解:因为多项式x2ym+1+xy2-2x3-5是六次四项式,
所以2+m+1=6,
所以m=3,
因为单项式6x2ny5–m的次数也是六次,
所以2n+5-m=6,
所以n=2,
所以m-n=3-2=1.
已知多项式是六次四项式,且的次数跟它相同.
(1)求m、n的值;
解:(1)因为多项式是六次四项式,
所以,
解得,,
5-m=5-3=2,
的次数与多项式的次数相同,
,解得,.
已知多项式是六次四项式,且的次数跟它相同.
(2)求多项式各项的系数和.
解:(2)各项的系数之和为:.
例3.如图,用式子表示圆环的面积.当R=15cm,r=10cm时,求圆环的面积(π取3.14).
解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是 .
当R=15cm,r=10cm时,圆环的面积(单位:cm2)是
这个圆环的面积是392.5cm2.
一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长L;
(2)花坛的面积S.
解:(1) L=2a+2πr
(2) 花坛的面积是一个长方形的面积与两个半圆的面积 之和,即S=2ar+ πr2
a
r
r
1.下列代数式,0,,,,,中,多项式的个数有( )
A.3个 B.4个 C.5个 D.6个
A
2.下列说法正确的是( )
A.单项式的系数是,次数是2 B.单项式的次数是3
C.是四次三项式 D.是二次单项式
C
4.如果一个多项式的次数是5,则这个多项式的任何一项的次数都( )
A.小于5 B.大于5 C.大于或等于5 D.小于或等于5
3.多项式的项数及次数分别是( )
A.3,2 B.3,3 C.2,3 D.3,4
D
D
5.若关于x的多项式是二次三项式,则a+b=_____.
6.关于x、y的多项式是四次二项式,则________.
7.已知关于x,y的多项式x2ym+1+xy2﹣2x3﹣5是六次四项式,单项式3x2ny5﹣m的次数与这个多项式的次数相同,则m﹣n=_____.
8.如果多项式不含和项,则______.
6
2或-3
1
-3
9.如图,文化广场上摆了一些桌子,若并排摆n张桌子,可同时容纳多少人 当n=20时,可同时容纳多少人
解: (1) 4×1+2,
(2) 4×2+2,
……
(n) 4n+2
当n=20时,4n+2=4×20+2
=82(人)
1.几个单项式的和叫做多项式;
2.在多项式中,每个单项式叫做多项式的项;
3.不含字母的项叫做常数项;
4.多项式里次数最高项的次数就是多项式的次数.
5.单项式与多项式统称为整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
