2.2.3 整式的加减 课件(共26张PPT)
文档属性
| 名称 | 2.2.3 整式的加减 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 09:17:30 | ||
图片预览









文档简介
(共36张PPT)
七上数学同步精品课件
人教版七年级上册
2.2.3 正式的加减
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第二章 整式的加减
1.熟练进行整式的加减运算.(重点)
2.能根据题意列出式子,表示问题中的数量关系.(难点)
1.合并同类项的法则是什么?
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
(1)括号外的因数是正数,去括号后式子各项的符号与原括号内式子相应各项的符号相同.
(2)括号外的因数是负数,去括号后式子各项的符号与原括号内式子相应各项的符号相反.
2.去括号的法则是什么?
化简下列各式:
(1) (2)
(3)
(2)解原式
;
(1)解原式
;
(3)解原式
=.
(2);
(1)
(1)解原式
;
例1.化简下列各式:
(2)解原式
;
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
例2.一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
你还能有其他解法吗?
解法二:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)+(2y+3y)
=7x+5y
例2.一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
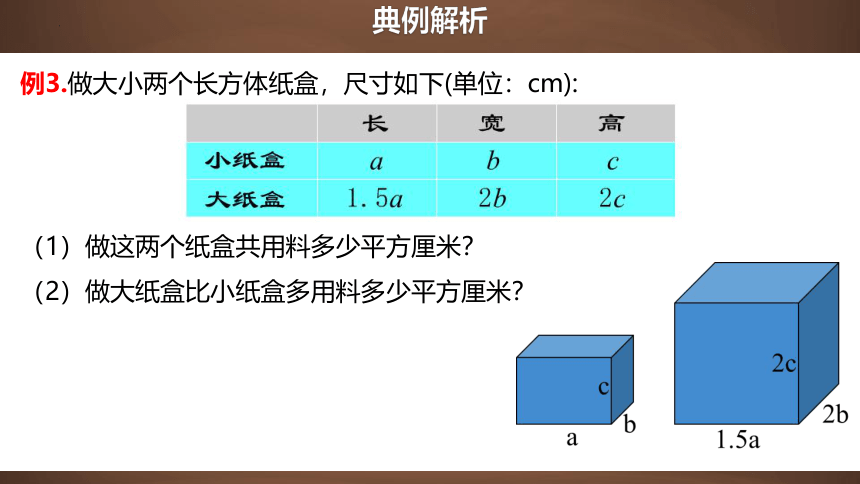
例3.做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
解:小纸盒的表面积是( )cm2
大纸盒的表面积是( )cm2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca(cm2 )
2ab+2bc+2ca
6ab+8bc+6ca
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)-(2ab+2bc+2ca)
=6ab+8bc+6ca-2ab-2bc-2ca
=4ab+6bc+4ca(cm )
2
【点睛】整式加减解决实际问题的一般步骤:
1.根据题意列代数式;2.去括号、合并同类项.;3.得出最后结果.
解:小纸盒的表面积是( )cm2
大纸盒的表面积是( )cm2
2ab+2bc+2ca
6ab+8bc+6ca
王奶奶是社区服务中心的热心自愿者,为了筹集公益基金,今年春天,她每天早晨从市果冻厂以每盒0.8元的价格购进a盒新鲜果冻,然后到人群聚集处以每盒1元的价格出售,平常白天一天可平均售出b盒果冻,双休日白天一天可多售出20%的果冻,每天晚上六点过后,王奶奶便将剩余的果冻降价处理,以每盒0.5元的价格全部卖完.
(1)请用含a、b的式子分别表示王奶奶平常每天的收入和双休日每天的收入;
解:(1﹣0.8)b+(0.5﹣0.8)(a﹣b)=0.2b﹣0.3a+0.3b=0.5b﹣0.3a;
(1﹣0.8)(1+20%)b+(0.5﹣0.8)[a﹣(1+20%)b)]
=0.24b+(-0.3)(a-1.2b)
=0.24b-0.3a+0.36b
=0.6b﹣0.3a;
答:王奶奶平常每天的收入为(0.5b﹣0.3a)元,双休日每天的收入为(0.6b﹣0.3a)元.
王奶奶是社区服务中心的热心自愿者,为了筹集公益基金,今年春天,她每天早晨从市果冻厂以每盒0.8元的价格购进a盒新鲜果冻,然后到人群聚集处以每盒1元的价格出售,平常白天一天可平均售出b盒果冻,双休日白天一天可多售出20%的果冻,每天晚上六点过后,王奶奶便将剩余的果冻降价处理,以每盒0.5元的价格全部卖完.
(2)王奶奶一个月(30天,含4个双休日)可收入多少元?(用含a、b式子表示)
(2)(0.5b﹣0.3a)×22+(0.6b﹣0.3a)×8
=11b﹣6.6a+4.8b﹣2.4a
=15.8b﹣9a;
答:王奶奶一个月可收入(15.8b﹣9a)元.
王奶奶是社区服务中心的热心自愿者,为了筹集公益基金,今年春天,她每天早晨从市果冻厂以每盒0.8元的价格购进a盒新鲜果冻,然后到人群聚集处以每盒1元的价格出售,平常白天一天可平均售出b盒果冻,双休日白天一天可多售出20%的果冻,每天晚上六点过后,王奶奶便将剩余的果冻降价处理,以每盒0.5元的价格全部卖完.
(3)当a=800,b=600时,求王奶奶平均每月实际可筹集多少元的公益基金?
(3)当a=800,b=600时,
15.8b﹣9a=15.8×600﹣9×800=9480﹣7200=2280(元),
答:王奶奶平均每月实际可筹集2280元的公益基金.
例4.先化简,再求值:,其中a,b满足.
解:原式
;
因为,
所以,,
例4.先化简,再求值:,其中a,b满足.
所以,,
原式
.
先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
解:因为|x+1|+(y﹣1)2=0,且|x+1|≥0,(y﹣1)2≥0,
所以x+1=0,y﹣1=0,
所以x=﹣1,y=1,
所以3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3
=3x2y+3xy﹣2x2y+2xy﹣4x2y﹣3
=﹣3x2y+5xy﹣3
=﹣3×(﹣1)2×1+5×(﹣1)×1﹣3
先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
=﹣3×1×1﹣5﹣3
=﹣3﹣5﹣3
=﹣11.
所以原式化简为﹣3x2y+5xy﹣3,代入求值结果为-11.
例5.已知A=﹣3x2﹣2mx+3x+1,B=2x2+2mx﹣1,且2A+3B的值与x无关,求m2﹣m的值.
解:2A+3B=2(﹣3x2﹣2mx+3x+1)+3(2x2+2mx﹣1)
=-6x2-4mx+6x+2+6x2+6mx-3
=(6+2m)x-1,
因为2A+3B的值与x无关,所以6+2m=0时,
解得m=-3,
当m=-3时m2﹣m=(﹣3)2﹣(﹣3)=12.
已知:,.
(1)求的值;
(2)若(1)中的代数式的值与a的取值无关,求b的值.
(1)解:因为,,
所以
;
(2)因为,代数式的值与a的取值无关,
所以,所以.
例6.已知a,b,c三个数在数轴上对应的点如图所示,
化简:
解:根据数轴可知:,|c|>|a|>|b|,
所以b-a<0,2a-b>0,a-c>0,
原式,
.
有理数,在数轴上对应点的位置如图所示,
化简
解:观察数轴得:,
所以,
所以
1.(3x2-2m+1)-(_______________) =5m2+m+3.
2.多项式a3-2a2+a-7减去5a2-2a+1的差是_______________.
3.单项式5x2,-7x2,-2x的和是___________.
4.如果m=1-n2,n=4a+3,a=-则m=____.
5.如果一个长方形的周长是4m+2n,其中一边长是2m-n,则另一边长为_____.
3x2-5m2-3m-2
a3-7a2+3a-8
-2x2-2x
0
2n
6.若A、B都是五次多项式,则A+B是( )
A.5次多项式 B.4次多项式
C.次数不低于5次的多项式 D.次数不高于5次的多项式或单项式
7.已知M=4x2-3x-2, N=6x2-3x+6, 则M与N的大小( )
A. MN C. M=N D.都不对
D
A
8.先化简,再求值:,其中,
.
解:
,
当,时,原式.
9.小马虎计算某多项式减去ab-3bc-2cd时,把减去看成加上,得到的答案为
-ab-2cd+3bc.请你求出这道题的正确结果.
解:这个多项式为:(-ab-2cd+3bc)-(ab-3bc-2cd)
=-ab-2cd+3bc-ab+3bc+2cd
=-ab-ab-2cd+2cd+3bc+3bc
=-2ab+6bc
因此,正确结果是:(-2ab+6bc)-(ab-3bc-2cd)
=-2ab+6bc-ab+3bc+2cd
=-2ab-ab+6bc+3bc+2cd=-3ab+9bc+2cd
10.已知代数式,.求的值,其中,.
解:因为,,
所以
,
将代入得,
原式.
11.阅读材料:对于任何数,我们规定符号的意义是,例如:.
(1)按照这个规定,请你计算的值;
(2)按照这个规定,请你计算当时,的值.
(1)解:
11.阅读材料:对于任何数,我们规定符号的意义是,例如:.
(2)按照这个规定,请你计算当时,的值.
(2)因为,
所以,,
所以,,
所以
12.某种型零件尺寸(左、右宽度相同)如图所示.
(1)求出阴影部分的周长(用含,的代数式表示);
(2)求出阴影部分的面积(用含,的代数式表示);
(3)当时,计算阴影部分的面积.
解:(1)
(2)
12.某种型零件尺寸(左、右宽度相同)如图所示.
(1)求出阴影部分的周长(用含,的代数式表示);
(2)求出阴影部分的面积(用含,的代数式表示);
(3)当时,计算阴影部分的面积.
(3)因为,
所以,,
得,.
当,时,阴影部分面积为
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
七上数学同步精品课件
人教版七年级上册
2.2.3 正式的加减
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第二章 整式的加减
1.熟练进行整式的加减运算.(重点)
2.能根据题意列出式子,表示问题中的数量关系.(难点)
1.合并同类项的法则是什么?
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
(1)括号外的因数是正数,去括号后式子各项的符号与原括号内式子相应各项的符号相同.
(2)括号外的因数是负数,去括号后式子各项的符号与原括号内式子相应各项的符号相反.
2.去括号的法则是什么?
化简下列各式:
(1) (2)
(3)
(2)解原式
;
(1)解原式
;
(3)解原式
=.
(2);
(1)
(1)解原式
;
例1.化简下列各式:
(2)解原式
;
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
例2.一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
你还能有其他解法吗?
解法二:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)+(2y+3y)
=7x+5y
例2.一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
例3.做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
解:小纸盒的表面积是( )cm2
大纸盒的表面积是( )cm2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca(cm2 )
2ab+2bc+2ca
6ab+8bc+6ca
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)-(2ab+2bc+2ca)
=6ab+8bc+6ca-2ab-2bc-2ca
=4ab+6bc+4ca(cm )
2
【点睛】整式加减解决实际问题的一般步骤:
1.根据题意列代数式;2.去括号、合并同类项.;3.得出最后结果.
解:小纸盒的表面积是( )cm2
大纸盒的表面积是( )cm2
2ab+2bc+2ca
6ab+8bc+6ca
王奶奶是社区服务中心的热心自愿者,为了筹集公益基金,今年春天,她每天早晨从市果冻厂以每盒0.8元的价格购进a盒新鲜果冻,然后到人群聚集处以每盒1元的价格出售,平常白天一天可平均售出b盒果冻,双休日白天一天可多售出20%的果冻,每天晚上六点过后,王奶奶便将剩余的果冻降价处理,以每盒0.5元的价格全部卖完.
(1)请用含a、b的式子分别表示王奶奶平常每天的收入和双休日每天的收入;
解:(1﹣0.8)b+(0.5﹣0.8)(a﹣b)=0.2b﹣0.3a+0.3b=0.5b﹣0.3a;
(1﹣0.8)(1+20%)b+(0.5﹣0.8)[a﹣(1+20%)b)]
=0.24b+(-0.3)(a-1.2b)
=0.24b-0.3a+0.36b
=0.6b﹣0.3a;
答:王奶奶平常每天的收入为(0.5b﹣0.3a)元,双休日每天的收入为(0.6b﹣0.3a)元.
王奶奶是社区服务中心的热心自愿者,为了筹集公益基金,今年春天,她每天早晨从市果冻厂以每盒0.8元的价格购进a盒新鲜果冻,然后到人群聚集处以每盒1元的价格出售,平常白天一天可平均售出b盒果冻,双休日白天一天可多售出20%的果冻,每天晚上六点过后,王奶奶便将剩余的果冻降价处理,以每盒0.5元的价格全部卖完.
(2)王奶奶一个月(30天,含4个双休日)可收入多少元?(用含a、b式子表示)
(2)(0.5b﹣0.3a)×22+(0.6b﹣0.3a)×8
=11b﹣6.6a+4.8b﹣2.4a
=15.8b﹣9a;
答:王奶奶一个月可收入(15.8b﹣9a)元.
王奶奶是社区服务中心的热心自愿者,为了筹集公益基金,今年春天,她每天早晨从市果冻厂以每盒0.8元的价格购进a盒新鲜果冻,然后到人群聚集处以每盒1元的价格出售,平常白天一天可平均售出b盒果冻,双休日白天一天可多售出20%的果冻,每天晚上六点过后,王奶奶便将剩余的果冻降价处理,以每盒0.5元的价格全部卖完.
(3)当a=800,b=600时,求王奶奶平均每月实际可筹集多少元的公益基金?
(3)当a=800,b=600时,
15.8b﹣9a=15.8×600﹣9×800=9480﹣7200=2280(元),
答:王奶奶平均每月实际可筹集2280元的公益基金.
例4.先化简,再求值:,其中a,b满足.
解:原式
;
因为,
所以,,
例4.先化简,再求值:,其中a,b满足.
所以,,
原式
.
先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
解:因为|x+1|+(y﹣1)2=0,且|x+1|≥0,(y﹣1)2≥0,
所以x+1=0,y﹣1=0,
所以x=﹣1,y=1,
所以3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3
=3x2y+3xy﹣2x2y+2xy﹣4x2y﹣3
=﹣3x2y+5xy﹣3
=﹣3×(﹣1)2×1+5×(﹣1)×1﹣3
先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
=﹣3×1×1﹣5﹣3
=﹣3﹣5﹣3
=﹣11.
所以原式化简为﹣3x2y+5xy﹣3,代入求值结果为-11.
例5.已知A=﹣3x2﹣2mx+3x+1,B=2x2+2mx﹣1,且2A+3B的值与x无关,求m2﹣m的值.
解:2A+3B=2(﹣3x2﹣2mx+3x+1)+3(2x2+2mx﹣1)
=-6x2-4mx+6x+2+6x2+6mx-3
=(6+2m)x-1,
因为2A+3B的值与x无关,所以6+2m=0时,
解得m=-3,
当m=-3时m2﹣m=(﹣3)2﹣(﹣3)=12.
已知:,.
(1)求的值;
(2)若(1)中的代数式的值与a的取值无关,求b的值.
(1)解:因为,,
所以
;
(2)因为,代数式的值与a的取值无关,
所以,所以.
例6.已知a,b,c三个数在数轴上对应的点如图所示,
化简:
解:根据数轴可知:,|c|>|a|>|b|,
所以b-a<0,2a-b>0,a-c>0,
原式,
.
有理数,在数轴上对应点的位置如图所示,
化简
解:观察数轴得:,
所以,
所以
1.(3x2-2m+1)-(_______________) =5m2+m+3.
2.多项式a3-2a2+a-7减去5a2-2a+1的差是_______________.
3.单项式5x2,-7x2,-2x的和是___________.
4.如果m=1-n2,n=4a+3,a=-则m=____.
5.如果一个长方形的周长是4m+2n,其中一边长是2m-n,则另一边长为_____.
3x2-5m2-3m-2
a3-7a2+3a-8
-2x2-2x
0
2n
6.若A、B都是五次多项式,则A+B是( )
A.5次多项式 B.4次多项式
C.次数不低于5次的多项式 D.次数不高于5次的多项式或单项式
7.已知M=4x2-3x-2, N=6x2-3x+6, 则M与N的大小( )
A. M
D
A
8.先化简,再求值:,其中,
.
解:
,
当,时,原式.
9.小马虎计算某多项式减去ab-3bc-2cd时,把减去看成加上,得到的答案为
-ab-2cd+3bc.请你求出这道题的正确结果.
解:这个多项式为:(-ab-2cd+3bc)-(ab-3bc-2cd)
=-ab-2cd+3bc-ab+3bc+2cd
=-ab-ab-2cd+2cd+3bc+3bc
=-2ab+6bc
因此,正确结果是:(-2ab+6bc)-(ab-3bc-2cd)
=-2ab+6bc-ab+3bc+2cd
=-2ab-ab+6bc+3bc+2cd=-3ab+9bc+2cd
10.已知代数式,.求的值,其中,.
解:因为,,
所以
,
将代入得,
原式.
11.阅读材料:对于任何数,我们规定符号的意义是,例如:.
(1)按照这个规定,请你计算的值;
(2)按照这个规定,请你计算当时,的值.
(1)解:
11.阅读材料:对于任何数,我们规定符号的意义是,例如:.
(2)按照这个规定,请你计算当时,的值.
(2)因为,
所以,,
所以,,
所以
12.某种型零件尺寸(左、右宽度相同)如图所示.
(1)求出阴影部分的周长(用含,的代数式表示);
(2)求出阴影部分的面积(用含,的代数式表示);
(3)当时,计算阴影部分的面积.
解:(1)
(2)
12.某种型零件尺寸(左、右宽度相同)如图所示.
(1)求出阴影部分的周长(用含,的代数式表示);
(2)求出阴影部分的面积(用含,的代数式表示);
(3)当时,计算阴影部分的面积.
(3)因为,
所以,,
得,.
当,时,阴影部分面积为
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
