2.3第二章 整式的加减章节复习 课件(共59张PPT)
文档属性
| 名称 | 2.3第二章 整式的加减章节复习 课件(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 09:25:01 | ||
图片预览










文档简介
(共59张PPT)
七上数学同步精品课件
人教版七年级上册
2. 3整式的加减章节复习
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第二章 整式的加减
1.知道单项式、多项式的相关概念;
2.知道同类项的概念,掌握合并同类项的方法;
3.运用整式的化简、求值,解决相关问题.
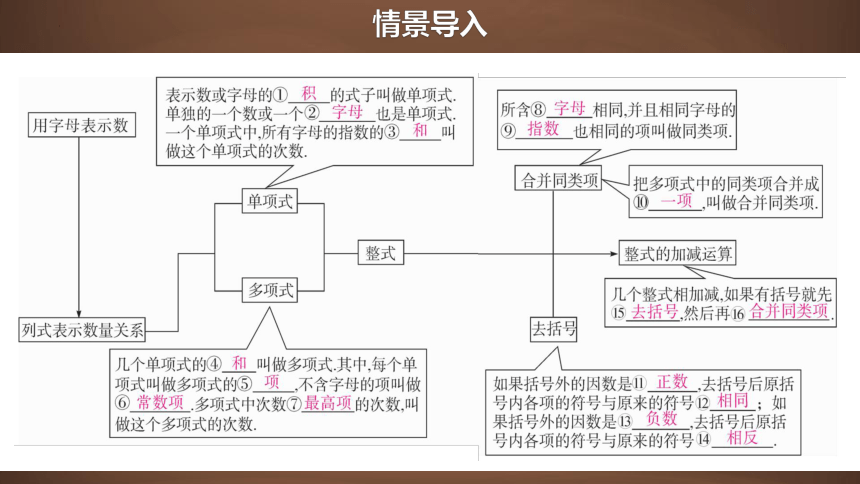
一、用字母表示数
列式时应注意:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
二、单项式及相关概念
1.单项式:表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
2.单项式的系数:单项式中的数字因数称为这个单项式的系数.
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
二、单项式及相关概念
在研究单项式的系数和次数问题时,要注意哪些问题:
2.圆周率π是常数.
3.单项式的系数应包括它前面的性质符号.
1.当单项式的系数是1或-1时,“1”通常省略不写.
系数问题
4.当单项式的系数不容易看出时,一定要先将单项式写成数×字母的形式.
次数问题
1.切记所有字母的指数的和.
2.当字母指数为1时,不要忽略.
=
二、单项式及相关概念
三、多项式及整式相关概念
1.多项式:几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
2.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
3.整式:单项式与多项式统称整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
三、多项式及整式相关概念
1.同类项:像100t与-252t,3x2与2x2,3ab2与-4ab2这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项. 几个常数项也是同类项. 例如5与-3.
四、同类项及合并同类项
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
2.同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
四、同类项及合并同类项
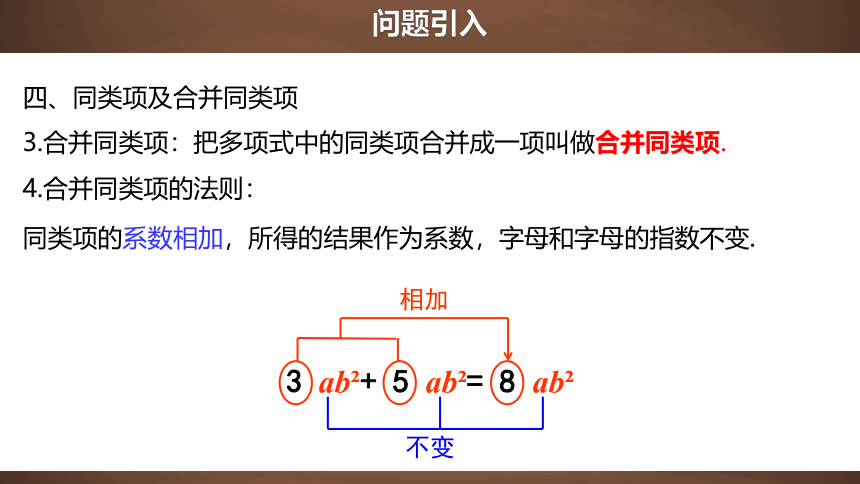
4.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
3.合并同类项:把多项式中的同类项合并成一项叫做合并同类项.
3 ab + 5 ab = 8 ab
相加
不变
5.“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
四、同类项及合并同类项
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
注意:
(1)去括号时,要连同括号前面的符号一起去掉;
(2)去括号时,首先要弄清楚括号前面是“+”号还是“-”号;
(3)注意“括号内各项的符号”的含义是指“各项都变号”或“都不变号”.
五、去括号法则
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
五、整式的加减
例1.在式子,,,,,,中,单项式有( )
A.3个 B.4个 C.5个 D.6个
【分析】解:是一个数字,是单项式;3x-y 式子中存在减法运算,不是单项式;
2 x y是数字与字母的乘积,是单项式;a是单独的一个字母是单项式;
式子中存在加法运算,不是单项式;πa2是单项式;
x+1式子中存在加法运算,不是单项式;故单项式一共有4个.
故选:B
B
单项式典型应用
1
单项式典型应用
1
例2.若是关于,的五次单项式且系数为6,试求,的值.
解:因为 是关于,的五次单项式且系数为6,
所以
所以
【1-1】关于单项式-23x2y2z, 下列结论中正确的是( )
A.系数是-2,次数是4 B.系数是-2,次数是5
C.系数是-2,次数是8 D.系数是-23,次数是5
D
【1-2】如果单项式头amb2n(m,n均为正整数)为六次单项式,那么m可以取的值为________,n可以取的值为________.
4或2
1或2
【1-3】已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
解:因为x2y|a|+(b+2)是关于x,y的五次单项式,
所以b+2=0,2+=5
所以a=±3,b=-2
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
例3.下列整式中哪些是多项式 是多项式的指出项和次数.
x2,y2,-1
2
3x2,-y,3xy3,x4,-1
4
2x,-y
1
多项式典型应用
2
例4.已知关于x,y的多项式x2ym+1+xy2–2x3–5是六次四项式,单项式
3x2ny5–m的次数与这个多项式的次数相同,求m-n的值.
解:因为多项式x2ym+1+xy2-2x3-5是六次四项式,
所以2+m+1=6,
所以m=3,
因为单项式6x2ny5–m的次数也是六次,
所以2n+5-m=6,
多项式典型应用
2
所以n=2,
所以m-n=3-2=1.
【2-1】下列代数式,0,,,,,中,多项式的个数有( )
A.3个 B.4个 C.5个 D.6个
A
【2-2】关于x、y的多项式是四次二项式,则________.
2或-3
【2-3】已知关于x,y的多项式x2ym+1+xy2﹣2x3﹣5是六次四项式,单项式3x2ny5﹣m的次数与这个多项式的次数相同,则m﹣n=_____.
1
例5.下列各组中的两项是不是同类项 为什么
(1)与 (2)与 (3)与
(4)与 (5)与 (6)与
【分析】(1)与中两项所含相同的字母的指数不同,不是同类项.
(2)与中两项所含的字母不同,不是同类项.
(3)与中两项所含字母相同,并且相同字母的指数也相同,是同类项.
(4)与中两项所含字母相同,并且相同字母的指数也相同,是同类项.
(5)与中两项不含相同字母,不是同类项.
(6)与中两项是常数项,是同类项
整式的加减运算
3
例6.化简下列各式:
(1)-2x-[x2-2(x2﹣3x)] (2)
(1)解原式=-2x-[x2-2(x2﹣3x)]
=-2x-(x2-2x2+6x)
=-2x-(-x2+6x)
=-2x+x2-6x
=x2-8x
(2)原式
整式的加减运算
3
例7.已知a,b,c三个数在数轴上对应的点如图所示,
化简:
解:根据数轴可知:,|c|>|a|>|b|,
所以b-a<0,2a-b>0,a-c>0,
原式,
.
整式的加减运算
3
【3-1】若3am+1b2与a3bn-1是同类项,则m=____,n=____.
2
3
【3-2】已知一个数为三位数,十位数字是a,个位数字比,a小2,百位数字是a的2倍,用式子表示这个数是( )
A.21a-2 B.211a-2 C.200a-2 D.3a-2
D
(2)解原式=5a2﹣[a2+5a2﹣2a﹣2a2+6a]
=5a2﹣(4a2+4a)
=a2﹣4a.
(1) (2)5a2﹣[a2+(5a2﹣2a)﹣2(a2﹣3a)]
(1)解原式
;
【3-3】化简下列各式:
【3-4】有理数,在数轴上对应点的位置如图所示,
化简
解:观察数轴得:,
所以,
所以
例8.先化简,再求值:,其中,
.
解:
,
当,时,原式.
整式的化简求值
4
例9.先化简,再求值:,其中a,b满足.
解:原式
;
因为,
所以,,
整式的化简求值
4
所以,,
原式
.
【4-1】先化简,再求值:,其中,.
解原式
当,时,原式.
【4-2】先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
解:因为|x+1|+(y﹣1)2=0,且|x+1|≥0,(y﹣1)2≥0,
所以x+1=0,y﹣1=0,
所以x=﹣1,y=1,
所以3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3
=3x2y+3xy﹣2x2y+2xy﹣4x2y﹣3
=﹣3x2y+5xy﹣3
=﹣3×(﹣1)2×1+5×(﹣1)×1﹣3
【4-2】先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
=﹣3×1×1﹣5﹣3
=﹣3﹣5﹣3
=﹣11.
所以原式化简为﹣3x2y+5xy﹣3,代入求值结果为-11.
整式的加减中无关型问题
5
例10.多项式的值与无关,求的值.
解:
,
∵多项式的值与无关,
∴,
解得:.
∴的值为.
例11.已知A=﹣3x2﹣2mx+3x+1,B=2x2+2mx﹣1,且2A+3B的值与x无关,求m2﹣m的值.
解:2A+3B=2(﹣3x2﹣2mx+3x+1)+3(2x2+2mx﹣1)
=-6x2-4mx+6x+2+6x2+6mx-3
=(6+2m)x-1,
因为2A+3B的值与x无关,所以6+2m=0时,
解得m=-3,
当m=-3时m2﹣m=(﹣3)2﹣(﹣3)=12.
整式的加减中无关型问题
5
【5-1】试说明:不论x取何值,代数式的值恒不变.
解:(x3+5x2+4x﹣1)﹣(﹣x2﹣3x+2x3﹣3)+(8﹣7x﹣6x2+x3)
=x3+5x2+4x﹣1+x2+3x﹣2x3+3+8﹣7x﹣6x2+x3
=x3﹣2x3+x3+5x2+x2﹣6x2+4x+3x﹣7x+10
=10,
∵此代数式恒等于10,
∴不论x取何值,代数式的值是不会改变的.
【5-2】学习了整式的加减运算后,张老师给同学们布置了一道课堂练习题“a=-10,b=2022时,求的值”.芳芳同学做完后对同桌说:“张老师给的条件b=2022是多余的,这道题不给的值,照样可以求出结果来.”同桌不相信她的话,亲爱的同学们,你相信芳芳的说法吗?说说你的理由.
解:(3a2b 2ab2+4a) 2(2a2b 3a)+2(ab2+a2b) 1
=3a2b-2ab2+4a-4a2b+6a+2ab2+a2b-1
=10a-1,
当a=-10时,原式=10×(-10)-1=-101.
化简结果中不含字母b,故最后的结果与b的取值无关,b=2022这个条件是多余的,
则芳芳同学的说法是正确的.
【5-3】已知,,若中不含一次项和常数项,求的值.
解:
∵计算结果不含有一次项和常数项,
∴,解得:,
∴
=-10
整式的加减实际应用
6
例12.2021年7月20日,郑州遭遇千年一遇的特大暴雨,面对严重汛情,社会各方力量纷纷赴郑救援.7月21日,为存放物资,现在要建一个三角形简易存放地,第一条边长为,第二条边比第一条边多,第三条边比第二条边短.
(1)求这个三角形周长(用含,的式子表示);
(1)解:因为第二条比第一条边长a-b,则第二条边长为:
(3a+2b)+(a-b)=4a+b,
所以第三条边比第二条边短2a,则第三条边长为:(4a+b)-2a=2a+b,
所以三角形周长是:(3a+2b)+(4a+b)+(2a+b)=9a+4b,
所以这个三角形周长是9a+4b;
整式的加减实际应用
6
例12.2021年7月20日,郑州遭遇千年一遇的特大暴雨,面对严重汛情,社会各方力量纷纷赴郑救援.7月21日,为存放物资,现在要建一个三角形简易存放地,第一条边长为,第二条边比第一条边多,第三条边比第二条边短.
(2)当m,m时,请你计算围成这个三角形存放地需要多少米材料?
(2)当a=230m,b=150m时,原式=9×230+4×150=2670(m),
所以围成这个三角形存放地需要2670米材料.
整式的加减实际应用
6
例13.一个三位数M,百位数字为a,十位数字为b,个位数字是c.
(1)请用含a,b,c的式子表示这个数M;
(2)现在把三位数M的百位数字,十位数字,个位数字分别交换到个位数字,百位数字,十位数字,得到一个新的三位数N,请用含a,b,c的式子表示N;
(3)请用含a,b,c的式子表示N-M,请判断N-M是否能被9整除?并说明理由.
(1)解:因为百位数字为a,十位数字为b,个位数字是c,
所以;
(2)因为百位数字为b,十位数字为c,个位数字是a,
所以;
整式的加减实际应用
6
例13.一个三位数M,百位数字为a,十位数字为b,个位数字是c.
(1)请用含a,b,c的式子表示这个数M;
(2)现在把三位数M的百位数字,十位数字,个位数字分别交换到个位数字,百位数字,十位数字,得到一个新的三位数N,请用含a,b,c的式子表示N;
(3)请用含a,b,c的式子表示N-M,请判断N-M是否能被9整除?并说明理由.
(3)因为
.
所以能被9整除.
【6-1】某轮船顺水航行,逆水航行,已知轮船在静水中的速度是,水流速度是.
(1)轮船顺水和逆水共航行多少千米?
(2)若,,求该轮船顺水航行的路程比逆水航行的路程多多少千米?
(1)解:根据题意得:
答:轮船顺水和逆水共航行千米
(2)根据题意得:
当,时,原式(千米)
答:轮船顺水航行的路程比逆水航行的路程多35千米.
【6-2】母亲节,阳阳送给妈妈一份精美的礼物,并用丝带把长方体礼品盒打上包装(如图所示,图中虚线为丝带),打蝴蝶结的部分需用丝带.
(1)用含、、的式子求出打好整个包装需用丝带总长度;
(2)若1米丝带费用为3元,求当,,时,(1)中丝带的总费用为多少元?
(1)解:由题意得打好整个包装需用丝带总长度为2x+4y+2z+(x-y+z)=2x+4y+2z+x-y+z=(3x+3y+3z)cm,答:打好整个包装需用丝带总长度为(3x+3y+3z)cm.
【6-2】母亲节,阳阳送给妈妈一份精美的礼物,并用丝带把长方体礼品盒打上包装(如图所示,图中虚线为丝带),打蝴蝶结的部分需用丝带.
(1)用含、、的式子求出打好整个包装需用丝带总长度;
(2)若1米丝带费用为3元,求当,,时,(1)中丝带的总费用为多少元?
(2)解:当,,时,3x+3y+3z=3×25+3×14+3×10=147(cm)147cm=1.47米,所需费用为1.47×3=4.41元,答:丝带的总费用为4.41元.
与整式的加减有关的探索性问题
7
例14.观察下列各式:﹣a,a2,﹣a3,a4,﹣a5,a6,…
(1)写出第2014个和2015个单项式;
(2)写出第n个单项式.
解:由﹣a,a2,﹣a3,a4,﹣a5,a6,…
可得第n项的表达式为(﹣1)n,
所以第2014个单项式为,第2015个单项式为﹣.
(2)由单项式的特点可得第n个单项式为(﹣1)n.
例15.设n表示自然数,用关于n的整式表示出来.从2开始连续的偶数相加,它们和的情况如下表:
加数的个数n 和s
1 2=1×2
2 2+4=6=2×3
3 2+4+6=12=3×4
4 2+4+6+8=20=4×5
…… ……
与整式的加减有关的探索性问题
7
⑴s与n之间有什么关系?能否用一个关系式来表示?
【分析】观察上表,当n=1时,s=1×2,即第一个数字是1,第二个数字是2;当n=2时,s=2+4=6=2×3,第一个数字是2,第二个数字是3,依此类推,发现第一个数字是n,第二个数字比n大1.
解:⑴s与n的关系为s=n(n+1).
解:当n= =1002时,
s=1002×(1002+1)=1005006.
即2+4+6+8+……+2004=1005006.
⑵计算2+4+6+8+……+2004.
与整式的加减有关的探索性问题
7
例16.用黑白两种颜色的正六边形地面砖中力所示的规律,拼成若干图案.
(1)第1个图形中有白色地砖 块;第2个图形中有白色地砖 块;第3个图形中有白色地砖 块;第4个图形中有白色地砖 块;
(1)解:第1个图形中有白色地砖6块,即4×1+2=6;
第2个图形中有白色地砖10块,即4×2+2=10;
第3个图形中有白色地砖14块,即4×3+2=14.
第4个图形中有白色地砖4×4+2=18(块);
与整式的加减有关的探索性问题
7
例16.用黑白两种颜色的正六边形地面砖中力所示的规律,拼成若干图案.
(2)求第n个图案中有白色地砖的块数,并求出n=100时白色地砖的块数.
(2)解:根据(1)可知:
第n个图案中,白色地砖共(4n+2)块.
所以n=100时,白色地砖共
4×100+2=402(块).
【7-1】观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:(1)因为当n=1时,xy,当n=2时,﹣3x2y,当n=3时,5x3y,当n=4时,﹣7x4y,当n=5时,9x5y,
所以第10个单项式是﹣(2×10﹣1) x10y,即﹣19x10y.
第2020个单项式是﹣(2×2020﹣1) x2020y,即﹣4039x2020y.
【7-1】观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:(2)因为n为奇数时,单项式的系数为正数,n为偶数时,单项式的系数为负数.
所以符合可用(﹣1)n+1表示,
因为系数的数字部分是连续的奇数,
所以可用2n﹣1来表示,
又因为第n个单项式的x的指数为n,y的指数不变,还是1,
所以第n个单项式可表示为(﹣1)n+1(2n﹣1)xny.
【7-2】如图,文化广场上摆了一些桌子,若并排摆n张桌子,可同时容纳多少人 当n=20时,可同时容纳多少人
解: (1) 4×1+2,
(2) 4×2+2,
……
(n) 4n+2
当n=20时,4n+2=4×20+2
=82(人)
6052
【7-3】观察下列图形:它们是按一定规律排列的,依照此规律,第2017个图形中共有________个五角星.
【解析】可以发现每个图形的五角星个数都比前面一个图形的五角星个数多3个.由于第1个图形的五角星个数是3×1+1,所以第n个图形的五角星个数是3n+1,故第2017个图形五角星个数是3×2017+1=6052.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
七上数学同步精品课件
人教版七年级上册
2. 3整式的加减章节复习
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第二章 整式的加减
1.知道单项式、多项式的相关概念;
2.知道同类项的概念,掌握合并同类项的方法;
3.运用整式的化简、求值,解决相关问题.
一、用字母表示数
列式时应注意:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
二、单项式及相关概念
1.单项式:表示数或字母的积的式,子叫做单项式.(单独的一个数或一个字母也是单项式).
2.单项式的系数:单项式中的数字因数称为这个单项式的系数.
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
二、单项式及相关概念
在研究单项式的系数和次数问题时,要注意哪些问题:
2.圆周率π是常数.
3.单项式的系数应包括它前面的性质符号.
1.当单项式的系数是1或-1时,“1”通常省略不写.
系数问题
4.当单项式的系数不容易看出时,一定要先将单项式写成数×字母的形式.
次数问题
1.切记所有字母的指数的和.
2.当字母指数为1时,不要忽略.
=
二、单项式及相关概念
三、多项式及整式相关概念
1.多项式:几个单项式的和叫做多项式. 其中,每个单项式叫做多项式的项,不含字母的项叫做常数项.
2.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
3.整式:单项式与多项式统称整式.
1.多项式的各项应包括它前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
4.一个多项式的最高次项可以不唯一.
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
在确定多项式的项和次数时应注意:
三、多项式及整式相关概念
1.同类项:像100t与-252t,3x2与2x2,3ab2与-4ab2这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项. 几个常数项也是同类项. 例如5与-3.
四、同类项及合并同类项
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
2.同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
四、同类项及合并同类项
4.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
3.合并同类项:把多项式中的同类项合并成一项叫做合并同类项.
3 ab + 5 ab = 8 ab
相加
不变
5.“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
四、同类项及合并同类项
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
注意:
(1)去括号时,要连同括号前面的符号一起去掉;
(2)去括号时,首先要弄清楚括号前面是“+”号还是“-”号;
(3)注意“括号内各项的符号”的含义是指“各项都变号”或“都不变号”.
五、去括号法则
3.运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2.整式加减实际上就是:去括号、合并同类项.
整式加减的一般步骤:
(1)如果有括号,那么先去括号;
(2)观察有无同类项;
(3)利用加法的交换律和结合律,分组同类项;
(4)合并同类项.
五、整式的加减
例1.在式子,,,,,,中,单项式有( )
A.3个 B.4个 C.5个 D.6个
【分析】解:是一个数字,是单项式;3x-y 式子中存在减法运算,不是单项式;
2 x y是数字与字母的乘积,是单项式;a是单独的一个字母是单项式;
式子中存在加法运算,不是单项式;πa2是单项式;
x+1式子中存在加法运算,不是单项式;故单项式一共有4个.
故选:B
B
单项式典型应用
1
单项式典型应用
1
例2.若是关于,的五次单项式且系数为6,试求,的值.
解:因为 是关于,的五次单项式且系数为6,
所以
所以
【1-1】关于单项式-23x2y2z, 下列结论中正确的是( )
A.系数是-2,次数是4 B.系数是-2,次数是5
C.系数是-2,次数是8 D.系数是-23,次数是5
D
【1-2】如果单项式头amb2n(m,n均为正整数)为六次单项式,那么m可以取的值为________,n可以取的值为________.
4或2
1或2
【1-3】已知x2y|a|+(b+2)是关于x、y的五次单项式,求a2﹣3ab的值.
解:因为x2y|a|+(b+2)是关于x,y的五次单项式,
所以b+2=0,2+=5
所以a=±3,b=-2
则当a=﹣3,b=﹣2时,a2﹣3ab=9﹣18=﹣9;
当a=3,b=﹣2时,a2﹣3ab=9+18=27.
例3.下列整式中哪些是多项式 是多项式的指出项和次数.
x2,y2,-1
2
3x2,-y,3xy3,x4,-1
4
2x,-y
1
多项式典型应用
2
例4.已知关于x,y的多项式x2ym+1+xy2–2x3–5是六次四项式,单项式
3x2ny5–m的次数与这个多项式的次数相同,求m-n的值.
解:因为多项式x2ym+1+xy2-2x3-5是六次四项式,
所以2+m+1=6,
所以m=3,
因为单项式6x2ny5–m的次数也是六次,
所以2n+5-m=6,
多项式典型应用
2
所以n=2,
所以m-n=3-2=1.
【2-1】下列代数式,0,,,,,中,多项式的个数有( )
A.3个 B.4个 C.5个 D.6个
A
【2-2】关于x、y的多项式是四次二项式,则________.
2或-3
【2-3】已知关于x,y的多项式x2ym+1+xy2﹣2x3﹣5是六次四项式,单项式3x2ny5﹣m的次数与这个多项式的次数相同,则m﹣n=_____.
1
例5.下列各组中的两项是不是同类项 为什么
(1)与 (2)与 (3)与
(4)与 (5)与 (6)与
【分析】(1)与中两项所含相同的字母的指数不同,不是同类项.
(2)与中两项所含的字母不同,不是同类项.
(3)与中两项所含字母相同,并且相同字母的指数也相同,是同类项.
(4)与中两项所含字母相同,并且相同字母的指数也相同,是同类项.
(5)与中两项不含相同字母,不是同类项.
(6)与中两项是常数项,是同类项
整式的加减运算
3
例6.化简下列各式:
(1)-2x-[x2-2(x2﹣3x)] (2)
(1)解原式=-2x-[x2-2(x2﹣3x)]
=-2x-(x2-2x2+6x)
=-2x-(-x2+6x)
=-2x+x2-6x
=x2-8x
(2)原式
整式的加减运算
3
例7.已知a,b,c三个数在数轴上对应的点如图所示,
化简:
解:根据数轴可知:,|c|>|a|>|b|,
所以b-a<0,2a-b>0,a-c>0,
原式,
.
整式的加减运算
3
【3-1】若3am+1b2与a3bn-1是同类项,则m=____,n=____.
2
3
【3-2】已知一个数为三位数,十位数字是a,个位数字比,a小2,百位数字是a的2倍,用式子表示这个数是( )
A.21a-2 B.211a-2 C.200a-2 D.3a-2
D
(2)解原式=5a2﹣[a2+5a2﹣2a﹣2a2+6a]
=5a2﹣(4a2+4a)
=a2﹣4a.
(1) (2)5a2﹣[a2+(5a2﹣2a)﹣2(a2﹣3a)]
(1)解原式
;
【3-3】化简下列各式:
【3-4】有理数,在数轴上对应点的位置如图所示,
化简
解:观察数轴得:,
所以,
所以
例8.先化简,再求值:,其中,
.
解:
,
当,时,原式.
整式的化简求值
4
例9.先化简,再求值:,其中a,b满足.
解:原式
;
因为,
所以,,
整式的化简求值
4
所以,,
原式
.
【4-1】先化简,再求值:,其中,.
解原式
当,时,原式.
【4-2】先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
解:因为|x+1|+(y﹣1)2=0,且|x+1|≥0,(y﹣1)2≥0,
所以x+1=0,y﹣1=0,
所以x=﹣1,y=1,
所以3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3
=3x2y+3xy﹣2x2y+2xy﹣4x2y﹣3
=﹣3x2y+5xy﹣3
=﹣3×(﹣1)2×1+5×(﹣1)×1﹣3
【4-2】先化简,再求值:3(x2y+xy)﹣2(x2y﹣xy)﹣4x2y﹣3,其中x、y满足|x+1|+(y﹣1)2=0.
=﹣3×1×1﹣5﹣3
=﹣3﹣5﹣3
=﹣11.
所以原式化简为﹣3x2y+5xy﹣3,代入求值结果为-11.
整式的加减中无关型问题
5
例10.多项式的值与无关,求的值.
解:
,
∵多项式的值与无关,
∴,
解得:.
∴的值为.
例11.已知A=﹣3x2﹣2mx+3x+1,B=2x2+2mx﹣1,且2A+3B的值与x无关,求m2﹣m的值.
解:2A+3B=2(﹣3x2﹣2mx+3x+1)+3(2x2+2mx﹣1)
=-6x2-4mx+6x+2+6x2+6mx-3
=(6+2m)x-1,
因为2A+3B的值与x无关,所以6+2m=0时,
解得m=-3,
当m=-3时m2﹣m=(﹣3)2﹣(﹣3)=12.
整式的加减中无关型问题
5
【5-1】试说明:不论x取何值,代数式的值恒不变.
解:(x3+5x2+4x﹣1)﹣(﹣x2﹣3x+2x3﹣3)+(8﹣7x﹣6x2+x3)
=x3+5x2+4x﹣1+x2+3x﹣2x3+3+8﹣7x﹣6x2+x3
=x3﹣2x3+x3+5x2+x2﹣6x2+4x+3x﹣7x+10
=10,
∵此代数式恒等于10,
∴不论x取何值,代数式的值是不会改变的.
【5-2】学习了整式的加减运算后,张老师给同学们布置了一道课堂练习题“a=-10,b=2022时,求的值”.芳芳同学做完后对同桌说:“张老师给的条件b=2022是多余的,这道题不给的值,照样可以求出结果来.”同桌不相信她的话,亲爱的同学们,你相信芳芳的说法吗?说说你的理由.
解:(3a2b 2ab2+4a) 2(2a2b 3a)+2(ab2+a2b) 1
=3a2b-2ab2+4a-4a2b+6a+2ab2+a2b-1
=10a-1,
当a=-10时,原式=10×(-10)-1=-101.
化简结果中不含字母b,故最后的结果与b的取值无关,b=2022这个条件是多余的,
则芳芳同学的说法是正确的.
【5-3】已知,,若中不含一次项和常数项,求的值.
解:
∵计算结果不含有一次项和常数项,
∴,解得:,
∴
=-10
整式的加减实际应用
6
例12.2021年7月20日,郑州遭遇千年一遇的特大暴雨,面对严重汛情,社会各方力量纷纷赴郑救援.7月21日,为存放物资,现在要建一个三角形简易存放地,第一条边长为,第二条边比第一条边多,第三条边比第二条边短.
(1)求这个三角形周长(用含,的式子表示);
(1)解:因为第二条比第一条边长a-b,则第二条边长为:
(3a+2b)+(a-b)=4a+b,
所以第三条边比第二条边短2a,则第三条边长为:(4a+b)-2a=2a+b,
所以三角形周长是:(3a+2b)+(4a+b)+(2a+b)=9a+4b,
所以这个三角形周长是9a+4b;
整式的加减实际应用
6
例12.2021年7月20日,郑州遭遇千年一遇的特大暴雨,面对严重汛情,社会各方力量纷纷赴郑救援.7月21日,为存放物资,现在要建一个三角形简易存放地,第一条边长为,第二条边比第一条边多,第三条边比第二条边短.
(2)当m,m时,请你计算围成这个三角形存放地需要多少米材料?
(2)当a=230m,b=150m时,原式=9×230+4×150=2670(m),
所以围成这个三角形存放地需要2670米材料.
整式的加减实际应用
6
例13.一个三位数M,百位数字为a,十位数字为b,个位数字是c.
(1)请用含a,b,c的式子表示这个数M;
(2)现在把三位数M的百位数字,十位数字,个位数字分别交换到个位数字,百位数字,十位数字,得到一个新的三位数N,请用含a,b,c的式子表示N;
(3)请用含a,b,c的式子表示N-M,请判断N-M是否能被9整除?并说明理由.
(1)解:因为百位数字为a,十位数字为b,个位数字是c,
所以;
(2)因为百位数字为b,十位数字为c,个位数字是a,
所以;
整式的加减实际应用
6
例13.一个三位数M,百位数字为a,十位数字为b,个位数字是c.
(1)请用含a,b,c的式子表示这个数M;
(2)现在把三位数M的百位数字,十位数字,个位数字分别交换到个位数字,百位数字,十位数字,得到一个新的三位数N,请用含a,b,c的式子表示N;
(3)请用含a,b,c的式子表示N-M,请判断N-M是否能被9整除?并说明理由.
(3)因为
.
所以能被9整除.
【6-1】某轮船顺水航行,逆水航行,已知轮船在静水中的速度是,水流速度是.
(1)轮船顺水和逆水共航行多少千米?
(2)若,,求该轮船顺水航行的路程比逆水航行的路程多多少千米?
(1)解:根据题意得:
答:轮船顺水和逆水共航行千米
(2)根据题意得:
当,时,原式(千米)
答:轮船顺水航行的路程比逆水航行的路程多35千米.
【6-2】母亲节,阳阳送给妈妈一份精美的礼物,并用丝带把长方体礼品盒打上包装(如图所示,图中虚线为丝带),打蝴蝶结的部分需用丝带.
(1)用含、、的式子求出打好整个包装需用丝带总长度;
(2)若1米丝带费用为3元,求当,,时,(1)中丝带的总费用为多少元?
(1)解:由题意得打好整个包装需用丝带总长度为2x+4y+2z+(x-y+z)=2x+4y+2z+x-y+z=(3x+3y+3z)cm,答:打好整个包装需用丝带总长度为(3x+3y+3z)cm.
【6-2】母亲节,阳阳送给妈妈一份精美的礼物,并用丝带把长方体礼品盒打上包装(如图所示,图中虚线为丝带),打蝴蝶结的部分需用丝带.
(1)用含、、的式子求出打好整个包装需用丝带总长度;
(2)若1米丝带费用为3元,求当,,时,(1)中丝带的总费用为多少元?
(2)解:当,,时,3x+3y+3z=3×25+3×14+3×10=147(cm)147cm=1.47米,所需费用为1.47×3=4.41元,答:丝带的总费用为4.41元.
与整式的加减有关的探索性问题
7
例14.观察下列各式:﹣a,a2,﹣a3,a4,﹣a5,a6,…
(1)写出第2014个和2015个单项式;
(2)写出第n个单项式.
解:由﹣a,a2,﹣a3,a4,﹣a5,a6,…
可得第n项的表达式为(﹣1)n,
所以第2014个单项式为,第2015个单项式为﹣.
(2)由单项式的特点可得第n个单项式为(﹣1)n.
例15.设n表示自然数,用关于n的整式表示出来.从2开始连续的偶数相加,它们和的情况如下表:
加数的个数n 和s
1 2=1×2
2 2+4=6=2×3
3 2+4+6=12=3×4
4 2+4+6+8=20=4×5
…… ……
与整式的加减有关的探索性问题
7
⑴s与n之间有什么关系?能否用一个关系式来表示?
【分析】观察上表,当n=1时,s=1×2,即第一个数字是1,第二个数字是2;当n=2时,s=2+4=6=2×3,第一个数字是2,第二个数字是3,依此类推,发现第一个数字是n,第二个数字比n大1.
解:⑴s与n的关系为s=n(n+1).
解:当n= =1002时,
s=1002×(1002+1)=1005006.
即2+4+6+8+……+2004=1005006.
⑵计算2+4+6+8+……+2004.
与整式的加减有关的探索性问题
7
例16.用黑白两种颜色的正六边形地面砖中力所示的规律,拼成若干图案.
(1)第1个图形中有白色地砖 块;第2个图形中有白色地砖 块;第3个图形中有白色地砖 块;第4个图形中有白色地砖 块;
(1)解:第1个图形中有白色地砖6块,即4×1+2=6;
第2个图形中有白色地砖10块,即4×2+2=10;
第3个图形中有白色地砖14块,即4×3+2=14.
第4个图形中有白色地砖4×4+2=18(块);
与整式的加减有关的探索性问题
7
例16.用黑白两种颜色的正六边形地面砖中力所示的规律,拼成若干图案.
(2)求第n个图案中有白色地砖的块数,并求出n=100时白色地砖的块数.
(2)解:根据(1)可知:
第n个图案中,白色地砖共(4n+2)块.
所以n=100时,白色地砖共
4×100+2=402(块).
【7-1】观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:(1)因为当n=1时,xy,当n=2时,﹣3x2y,当n=3时,5x3y,当n=4时,﹣7x4y,当n=5时,9x5y,
所以第10个单项式是﹣(2×10﹣1) x10y,即﹣19x10y.
第2020个单项式是﹣(2×2020﹣1) x2020y,即﹣4039x2020y.
【7-1】观察下列一串单项式的特点: , , , , ,…
(1)写出第10个和第2020个单项式.
(2)写出第n个单项式.
解:(2)因为n为奇数时,单项式的系数为正数,n为偶数时,单项式的系数为负数.
所以符合可用(﹣1)n+1表示,
因为系数的数字部分是连续的奇数,
所以可用2n﹣1来表示,
又因为第n个单项式的x的指数为n,y的指数不变,还是1,
所以第n个单项式可表示为(﹣1)n+1(2n﹣1)xny.
【7-2】如图,文化广场上摆了一些桌子,若并排摆n张桌子,可同时容纳多少人 当n=20时,可同时容纳多少人
解: (1) 4×1+2,
(2) 4×2+2,
……
(n) 4n+2
当n=20时,4n+2=4×20+2
=82(人)
6052
【7-3】观察下列图形:它们是按一定规律排列的,依照此规律,第2017个图形中共有________个五角星.
【解析】可以发现每个图形的五角星个数都比前面一个图形的五角星个数多3个.由于第1个图形的五角星个数是3×1+1,所以第n个图形的五角星个数是3n+1,故第2017个图形五角星个数是3×2017+1=6052.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
