22.3.2 实际问题与二次函数(二)-商品利润最大问题 课件(共32张PPT)
文档属性
| 名称 | 22.3.2 实际问题与二次函数(二)-商品利润最大问题 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 09:22:49 | ||
图片预览










文档简介
(共32张PPT)
九上数学同步优质课件
人教版九年级上册
实际问题与二次函数
(二) 商品利润最大问题
第二十二章 二次函数
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.(重点)
2.弄清商品销售问题中的数量关系及确定自变量的取值范围. (难点)
1.二次函数y=2x2-8x+1图象的顶点坐标是________,当x=____时,y的最小值为____.
2.某旅行社要接团去外地旅游,经计算所获利润y(元)与旅行团人数x(人)满足关系式y=-x2+100x.
(1)二次函数y=-x2+100x的图象开口向___,有最___值,为_____;
(2)要使旅行团所获利润最大,则此时旅行团应有___人.
(2,-7)
2
-7
下
大
2500
50
利润问题
一.几个量之间的关系.
二.在商品销售中,通常采用哪些方法增加利润?
1.总价、单价、数量的关系:总价=单价×数量
2.利润、售价、进价的关系:利润=售价-进价
3.总利润、单件利润、数量的关系:总利润=单件利润×数量
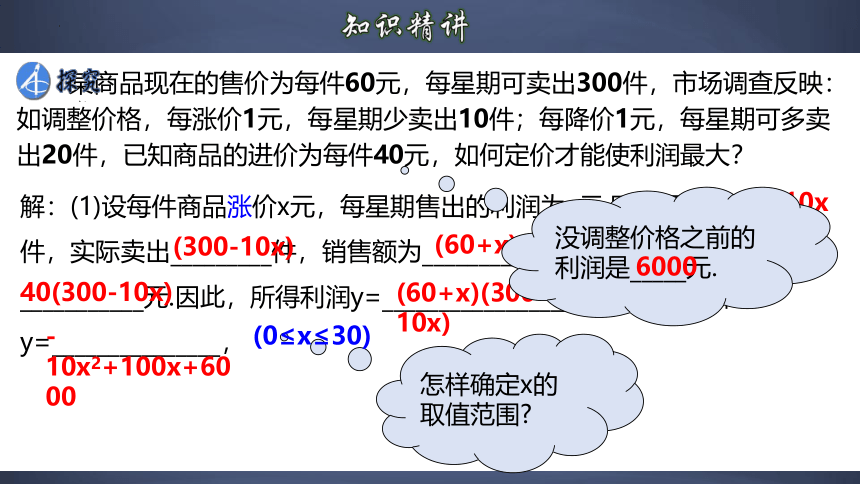
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
解:(1)设每件商品涨价x元,每星期售出的利润为y元.则每星期少卖_____件,实际卖出_________件,销售额为_______________元,买进商品需付___________元.因此,所得利润y=___________________________,即y=_______________,
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
(60+x)(300-10x)-40(300-10x)
-10x2+100x+6000
怎样确定x的取值范围
(0≤x≤30)
没调整价格之前的利润是_____元.
6000
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
方法2:
设每件商品涨价x元,每星期售出的利润为y元.则每件利润是_________元,每星期少卖____件,实际卖出__________件,因此,所得利润y=___________________即y=_________________,(0≤x≤30).
(60-40+x)
10x
(300-10x)
(60-40+x)(300-10x)
-10x2+100x+6000
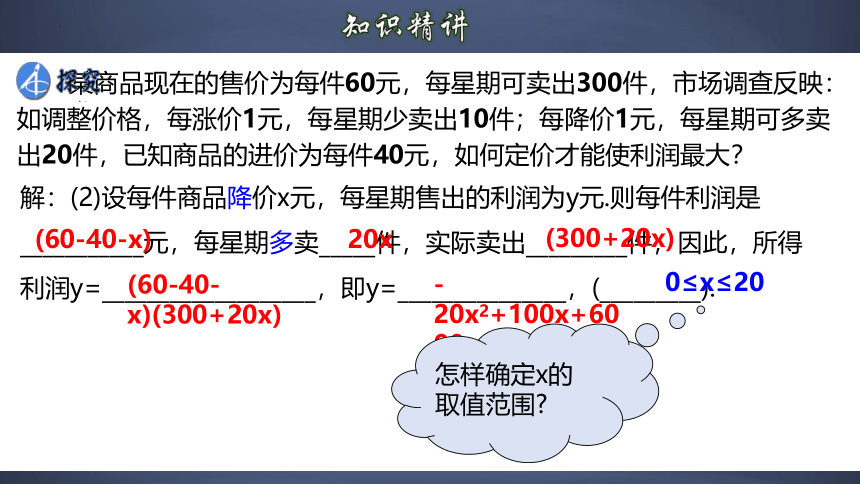
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
5
解:(1)设每件商品涨价x元,每星期售出的利润为y元.
y=-10x2+100x+6000,其中,0≤x≤30.
根据上面的函数,填空:
当x=____时,y最大,也就是说,在涨价的情况下,涨价____元,即定价_____元时,利润最大,最大利润是______元.
5
65
6250
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
解:(2)设每件商品降价x元,每星期售出的利润为y元.则每件利润是___________元,每星期多卖_____件,实际卖出_________件,因此,所得利润y=___________________,即y=_______________,(_________).
20x
(300+20x)
(60-40-x)(300+20x)
(60-40-x)
-20x2+100x+6000
0≤x≤20
怎样确定x的取值范围
解:(2)设每件商品降价x元,每星期售出的利润为y元.
y=-20x2+100x+6000,其中,0≤x≤20.
根据上面的函数,填空:
当x=____时,y最大,也就是说,在降价的情况下,降价____元,即定价_____元时,利润最大,最大利润是______元.
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
2.5
2.5
57.5
6125
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
(1)涨价5元,即定价65元时,利润最大,最大利润是6250元;
(2)降价2.5元,即定价57.5元时,利润最大,最大利润是6125元.
当定价为65元时,能使利润最大,最大利润是6250元.
由(1)(2)的讨论及现在的销售情况,你知道应如何定价能使利润最大了吗?
例1.某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=-2x+180.为保证市场稳定,供货商规定销售价格不得低于75元/件且不得高于90元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式;
(2)每件小电器的销售价格定为多少元时,才能使每天获得的利润最大,最大是多少元?
解:(1)由题意可得w=(x-45-5)(-2x+180)=-2x2+280x-9000
(2)w=-2x2+280x-9000=-2(x-70)2+800
∵ 销售价格不得低于75元/件且不得高于90元/件
∴ 75≤x≤90
∵ -2<0,∴ 当75≤x≤90时,w随x的增大而减小
∴ 当x=75时,有最大利润,最大利润为750元
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件. 那么,涨价多少元时,一个月内利润最大,最大利润是多少?
解:设每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,根据题意,得
y=(30-20+x)(180-10x)
即:y=-10x2+80x+1800=-10(x-4)2+1960
∵ -10<0,∴ 当x=4时,y取最大值1960元
答:涨价4元时,一个月内利润最大,最大利润为1960元.
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量?
(2)求出y与x的函数关系式?
(3)该经销店要想获得最大利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗 请说明理由.
解:(1) 45+×7.5=60(吨)
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(2)求出y与x的函数关系式?
解:(2)y=(x-100)(45+×7.5)
即y=-x2+315x-24000
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(3)该经销店要想获得最大利润,售价应定为每吨多少元?
解:(3)y=-x2+315x-24000
∵a=-
∴当x=210时,y最大=9075
即当售价定为210元时,经销店获得最大月利润9075元.
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗 请说明理由.
解:(4)不对,
理由:当月利润最大时,x=210,此时,月销售额为17325元;
而当x=200时,月销售额为18000元
∵17325<18000,
∴当月利润最大时,月销售额不是最大.小静说的不对.
例3.春暖花开,树木萌芽,某种时令蔬菜的价格呈上升趋势.若这种蔬菜开始时的售价为每千克20元,并且每天涨价2元,从第6天开始,保持每千克30元的稳定价格销售,直到第11天结束,该蔬菜退市.
(1)请写出该种蔬菜销售价格y(元/千克)与天数x之间的函数关系式;
解:(1)该种蔬菜销售价格y(元/千克)与天数x之间的函数关系式为
(2)若该种蔬菜于进货当天售完,且这种蔬菜每千克进价z(元)与天数x的关系为z=(x-8)2+12(1≤x≤11,且x为整数),那么该种蔬菜在第几天售出后,每千克获得利润最大 最大利润为多少
解:(2)设利润为w,
由①w=x2+14 (1≤x<6,x为整数)
∵>0 ∴当x>0时,w随x的增大而增大∴当x=5时,W最大=+14=17.125(元)
解:(2)设利润为w,
由②w=(x-8)2+18 (6≤x≤11,x为整数)
∴当x=11时,w最大=+18=19.125
∵17.125<19.125
∴在第11天进货并售出后,每千克所获利润最大,最大利润为19.125元.
1.某鞋帽专卖店销售一种绒帽.若这种帽子每天获利y(元)与销售单价x(元)满足关系y=-x2+70x-800,要想获得最大利润,则销售单价为( )
A.30元 B.35元 C.40元 D.45元
2.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x ≤19,那么一周可获得最大利润是( )
A.1554元 B.1556元 C.1558元 D.1560元
B
B
3.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,当一天出售该种手工艺品的总额利润y最大,x的值为( )
A.1 B.2 C.3 D.4
4.某产品每件的成本是120元,试销阶段每件的销售价x(元)与产品日销售量y(件)之间的关系是y=-x+200,为获得最大的销售利润,每件产品的销售价应定为( )
A.120元 B.130元 C.150元 D.160元
D
D
5.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高0.5元,销售量相应减少10件.如何提高售价,才能在半个月内获得最大利润
解:设销售单价提高x元,半个月内销售利润为y元,依题意得
y=(x+30-20)(400-x)
即y=-20(x-5)2+4500(O≤x≤20)
因此,当x=5时,y最大=4500.
答:当售价提高5元,即销售单价为35元时,半个月内可获得最大利润4500元.
6.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件.假定每月销售件数m(件)是价格x(元/件)的一次函数.
(1)试求出m与x之间的函数解析式.
(1)解:设m=kx+b,根据题意,得
解得
∴m=-30x+960
6.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件.假定每月销售件数m(件)是价格x(元/件)的一次函数.
(1)试求出m与x之间的函数解析式.(m=-30x+960)
(2)问销售价格定为多少时,才能使每月获得最大利润 每月的最大利润y(元)是多少
解:(2)依题意得,y=(x-16)(-30x+960)
即y=-30x2+1440x-15360
∵a=-30<0,∴当x=-=24时,y最大=1920
即价格定为24元时,每月获得最大利润为1920元.
x
y
5
16
O
7
7.某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由图象可求y=-x2+20x-75,
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最大,为25元.
(2)由对称性知y=16时,x=7和13.
故销售单价在7 ≤x ≤13时,利润不低于16元.
7.某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
x
y
5
16
O
7
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
实际问题与二次函数
(二) 商品利润最大问题
第二十二章 二次函数
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.(重点)
2.弄清商品销售问题中的数量关系及确定自变量的取值范围. (难点)
1.二次函数y=2x2-8x+1图象的顶点坐标是________,当x=____时,y的最小值为____.
2.某旅行社要接团去外地旅游,经计算所获利润y(元)与旅行团人数x(人)满足关系式y=-x2+100x.
(1)二次函数y=-x2+100x的图象开口向___,有最___值,为_____;
(2)要使旅行团所获利润最大,则此时旅行团应有___人.
(2,-7)
2
-7
下
大
2500
50
利润问题
一.几个量之间的关系.
二.在商品销售中,通常采用哪些方法增加利润?
1.总价、单价、数量的关系:总价=单价×数量
2.利润、售价、进价的关系:利润=售价-进价
3.总利润、单件利润、数量的关系:总利润=单件利润×数量
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
解:(1)设每件商品涨价x元,每星期售出的利润为y元.则每星期少卖_____件,实际卖出_________件,销售额为_______________元,买进商品需付___________元.因此,所得利润y=___________________________,即y=_______________,
10x
(300-10x)
(60+x)(300-10x)
40(300-10x)
(60+x)(300-10x)-40(300-10x)
-10x2+100x+6000
怎样确定x的取值范围
(0≤x≤30)
没调整价格之前的利润是_____元.
6000
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
方法2:
设每件商品涨价x元,每星期售出的利润为y元.则每件利润是_________元,每星期少卖____件,实际卖出__________件,因此,所得利润y=___________________即y=_________________,(0≤x≤30).
(60-40+x)
10x
(300-10x)
(60-40+x)(300-10x)
-10x2+100x+6000
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
5
解:(1)设每件商品涨价x元,每星期售出的利润为y元.
y=-10x2+100x+6000,其中,0≤x≤30.
根据上面的函数,填空:
当x=____时,y最大,也就是说,在涨价的情况下,涨价____元,即定价_____元时,利润最大,最大利润是______元.
5
65
6250
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
解:(2)设每件商品降价x元,每星期售出的利润为y元.则每件利润是___________元,每星期多卖_____件,实际卖出_________件,因此,所得利润y=___________________,即y=_______________,(_________).
20x
(300+20x)
(60-40-x)(300+20x)
(60-40-x)
-20x2+100x+6000
0≤x≤20
怎样确定x的取值范围
解:(2)设每件商品降价x元,每星期售出的利润为y元.
y=-20x2+100x+6000,其中,0≤x≤20.
根据上面的函数,填空:
当x=____时,y最大,也就是说,在降价的情况下,降价____元,即定价_____元时,利润最大,最大利润是______元.
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
2.5
2.5
57.5
6125
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
(1)涨价5元,即定价65元时,利润最大,最大利润是6250元;
(2)降价2.5元,即定价57.5元时,利润最大,最大利润是6125元.
当定价为65元时,能使利润最大,最大利润是6250元.
由(1)(2)的讨论及现在的销售情况,你知道应如何定价能使利润最大了吗?
例1.某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=-2x+180.为保证市场稳定,供货商规定销售价格不得低于75元/件且不得高于90元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式;
(2)每件小电器的销售价格定为多少元时,才能使每天获得的利润最大,最大是多少元?
解:(1)由题意可得w=(x-45-5)(-2x+180)=-2x2+280x-9000
(2)w=-2x2+280x-9000=-2(x-70)2+800
∵ 销售价格不得低于75元/件且不得高于90元/件
∴ 75≤x≤90
∵ -2<0,∴ 当75≤x≤90时,w随x的增大而减小
∴ 当x=75时,有最大利润,最大利润为750元
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件. 那么,涨价多少元时,一个月内利润最大,最大利润是多少?
解:设每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,根据题意,得
y=(30-20+x)(180-10x)
即:y=-10x2+80x+1800=-10(x-4)2+1960
∵ -10<0,∴ 当x=4时,y取最大值1960元
答:涨价4元时,一个月内利润最大,最大利润为1960元.
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量?
(2)求出y与x的函数关系式?
(3)该经销店要想获得最大利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗 请说明理由.
解:(1) 45+×7.5=60(吨)
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(2)求出y与x的函数关系式?
解:(2)y=(x-100)(45+×7.5)
即y=-x2+315x-24000
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(3)该经销店要想获得最大利润,售价应定为每吨多少元?
解:(3)y=-x2+315x-24000
∵a=-
∴当x=210时,y最大=9075
即当售价定为210元时,经销店获得最大月利润9075元.
例2.利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其他费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗 请说明理由.
解:(4)不对,
理由:当月利润最大时,x=210,此时,月销售额为17325元;
而当x=200时,月销售额为18000元
∵17325<18000,
∴当月利润最大时,月销售额不是最大.小静说的不对.
例3.春暖花开,树木萌芽,某种时令蔬菜的价格呈上升趋势.若这种蔬菜开始时的售价为每千克20元,并且每天涨价2元,从第6天开始,保持每千克30元的稳定价格销售,直到第11天结束,该蔬菜退市.
(1)请写出该种蔬菜销售价格y(元/千克)与天数x之间的函数关系式;
解:(1)该种蔬菜销售价格y(元/千克)与天数x之间的函数关系式为
(2)若该种蔬菜于进货当天售完,且这种蔬菜每千克进价z(元)与天数x的关系为z=(x-8)2+12(1≤x≤11,且x为整数),那么该种蔬菜在第几天售出后,每千克获得利润最大 最大利润为多少
解:(2)设利润为w,
由①w=x2+14 (1≤x<6,x为整数)
∵>0 ∴当x>0时,w随x的增大而增大∴当x=5时,W最大=+14=17.125(元)
解:(2)设利润为w,
由②w=(x-8)2+18 (6≤x≤11,x为整数)
∴当x=11时,w最大=+18=19.125
∵17.125<19.125
∴在第11天进货并售出后,每千克所获利润最大,最大利润为19.125元.
1.某鞋帽专卖店销售一种绒帽.若这种帽子每天获利y(元)与销售单价x(元)满足关系y=-x2+70x-800,要想获得最大利润,则销售单价为( )
A.30元 B.35元 C.40元 D.45元
2.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x ≤19,那么一周可获得最大利润是( )
A.1554元 B.1556元 C.1558元 D.1560元
B
B
3.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,当一天出售该种手工艺品的总额利润y最大,x的值为( )
A.1 B.2 C.3 D.4
4.某产品每件的成本是120元,试销阶段每件的销售价x(元)与产品日销售量y(件)之间的关系是y=-x+200,为获得最大的销售利润,每件产品的销售价应定为( )
A.120元 B.130元 C.150元 D.160元
D
D
5.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高0.5元,销售量相应减少10件.如何提高售价,才能在半个月内获得最大利润
解:设销售单价提高x元,半个月内销售利润为y元,依题意得
y=(x+30-20)(400-x)
即y=-20(x-5)2+4500(O≤x≤20)
因此,当x=5时,y最大=4500.
答:当售价提高5元,即销售单价为35元时,半个月内可获得最大利润4500元.
6.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件.假定每月销售件数m(件)是价格x(元/件)的一次函数.
(1)试求出m与x之间的函数解析式.
(1)解:设m=kx+b,根据题意,得
解得
∴m=-30x+960
6.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件.假定每月销售件数m(件)是价格x(元/件)的一次函数.
(1)试求出m与x之间的函数解析式.(m=-30x+960)
(2)问销售价格定为多少时,才能使每月获得最大利润 每月的最大利润y(元)是多少
解:(2)依题意得,y=(x-16)(-30x+960)
即y=-30x2+1440x-15360
∵a=-30<0,∴当x=-=24时,y最大=1920
即价格定为24元时,每月获得最大利润为1920元.
x
y
5
16
O
7
7.某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由图象可求y=-x2+20x-75,
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最大,为25元.
(2)由对称性知y=16时,x=7和13.
故销售单价在7 ≤x ≤13时,利润不低于16元.
7.某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
x
y
5
16
O
7
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
