22.3.3 实际问题与二次函数(三)-拱桥问题中的抛物线 课件(共23张PPT)
文档属性
| 名称 | 22.3.3 实际问题与二次函数(三)-拱桥问题中的抛物线 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 09:25:23 | ||
图片预览







文档简介
(共23张PPT)
九上数学同步优质课件
人教版九年级上册
实际问题与二次函数
(三) 拱桥问题中的抛物线
第二十二章 二次函数
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.(重点)
2.利用二次函数解决拱桥及运动中的有关问题.(重、难点)
3.能运用二次函数的图象与性质进行决策.
1.函数y=ax2(a≠0)的图象是一条_______,它的顶点坐标是_______,对称轴是_____,当a____时,开口向上,当a____时,开口向下.
2.二次函数解析式的形式有:
①一般式:____________,
②顶点式:_____________,
③交点式:________________.
3.(1)如图所示的抛物线,可以根据顶点所在的位置设为_________,也可以根据抛物线与x轴的交点坐标设为______________.
(2)由A,B两点的横坐标,可以求得线段AB的长
为______.
抛物线
(0,0)
y轴
>0
<0
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
y=ax2+2
y=a(x+2)(x-2)
4
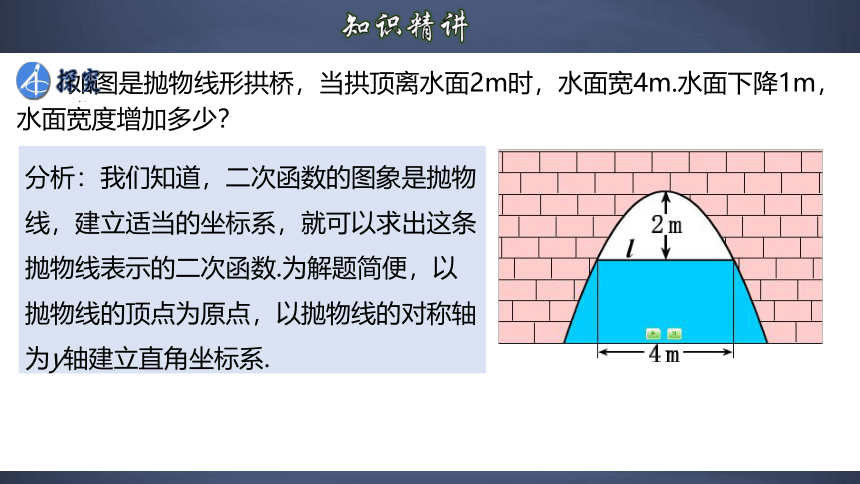
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
解:以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设这条抛物线表示的二次函数为y=ax2.由抛物线经过点(2,-2),可得
-2=a×22,解得,a=-
∴ 这条抛物线表示的二次函数为:y=-x2
当水面下降1m时,水面的纵坐标为-3.
当y=-3时,x=±.
∴当水面下降1m时,水面的宽度为2m.
∴水面的宽度增加了(2-4)m.
你有其它解法吗?
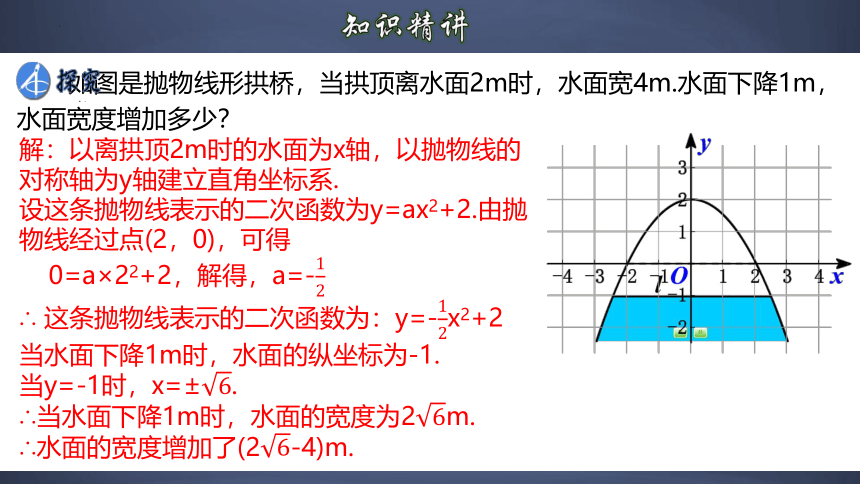
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
解:以离拱顶2m时的水面为x轴,以抛物线的对称轴为y轴建立直角坐标系.
设这条抛物线表示的二次函数为y=ax2+2.由抛物线经过点(2,0),可得
0=a×22+2,解得,a=-
∴ 这条抛物线表示的二次函数为:y=-x2+2
当水面下降1m时,水面的纵坐标为-1.
当y=-1时,x=±.
∴当水面下降1m时,水面的宽度为2m.
∴水面的宽度增加了(2-4)m.
在“拱桥类”问题中,一般知道拱高和拱长,这时可根据抛物线的对称性建立以对称轴为y轴的坐标系,然后根据所建立的坐标系,确定抛物线上一些点的坐标.若顶点在原点上,一般设二次函数的解析式为y=ax2;若顶点不在原点上,一般设二次函数的解析式为y=ax2+k.
步骤:
(1)恰当地建立直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数关系式;
(4)代入已知条件或点的坐标求出关系式;
(5)利用关系式求解问题.
例1.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-0.25x2+4表示.
(1)一辆高5.2m,宽2m的货运卡车能通过该隧道吗
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过
解:(1)建立相应的坐标系.当货运卡车在正中央时,
即对应的x=±1,y=3.75.
∵3.75+2>5.2
∴它能通过该隧道
(2)当隧道内设双行道时,就意味着货运卡车只能走一边,即对应的x=±2,y=3.
∵3+2<5.2
∴它不能通过该隧道.
例2.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管如图做成的立柱,为了计算所需不锈钢立柱的总长度,设计人员测得如图所示的数据.
(1)求该抛物线的解析式;
(2)计算所需不锈钢管的总长度.
解:(1)以0为原点建立直角坐标.
设此抛物线解析式为y=ax(x-2),
依题意得,抛物线顶点坐标为(1,0.5)
∴0.5=a×1×(1-2),解得a=-
∴该抛物线的解析式为y=-x(x-2),即y=-x2+x.
例2.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管如图做成的立柱,为了计算所需不锈钢立柱的总长度,设计人员测得如图所示的数据.
(1)求该抛物线的解析式; y=-x2+x
(2)计算所需不锈钢管的总长度.
解:(2)依题意得:
当x=0.4时,y=0.32
当x=0.8时,y=0.48
当x=1.2时,y=0.48
当x=1.6时,y=0.32
所需不锈钢管的总长度为50×2×(0.32+0.48)=80m.
例3.如图,已知排球场的长度OD为18米,位于球场中线处的球网AB的高度2.24米,一队员站在点0处发球,排球从点0的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点0的水平距离OE为6米时,到达最高点G,以0为原点建立如图所示的平面直角坐标系.
(1)若排球运行的最大高度为2.8米,求排球飞行的高度p(单位:米)与水平距离x(单位:米)之间的函数关系式;
解:(1)由题意知顶点G的坐标为(6,2.8),则设抛物线的解析式为p=a(x-6)2+2.8
∵点C坐标为(0,2),且在抛物线上
∴2=a(0-6)2+2.8,解得a=-.
∴p=-(x-6)2+2.8
例3.如图,已知排球场的长度OD为18米,位于球场中线处的球网AB的高度2.24米,一队员站在点0处发球,排球从点0的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点0的水平距离OE为6米时,到达最高点G,以0为原点建立如图所示的平面直角坐标系.
(2)在(1)的条件下,这次所发的球能够过网吗 如果能够过网,是否会出界 请说明理由;
解:(2)当x=9时,p=-×(9-6)2+2.8
=2.6>2.24
当x=18时,p=-×(18-6)2+2.8=-0.4<0
故这次发球可以过网且不出边界
(3)若该队员发球要想过网,又使排球不会出界(排球压线属于没出界),求二次函数中二次项系数的最大值.
解:(3)设抛物线的解析式为p=a(x-6)2+h
将点C(0,2)代入得36a+h=2,即h=2-36a
∴p=a(x-6)2+2-36a
根据题意,不出边界时有
a(18-6)2+2-36a≤0,解得a≤-
要使排球过网,则a(9-6)2+2-36a≥2.24,解得a≤-故二次函数中二次项系数的最大值为-
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在____s后落地.
2.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是____米.
4
4
3.有一个抛物线形桥拱,其最大高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系中(如右图),则此抛物线的解析式为__________________.
4.在一次羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线y=-元2+bx+c的一部分(如图),其中出球点B离地面0点的距离是1m,球落地点A到0点的距离是4m,那么这条抛物线的解析式为_____________.
y=-0.04(x-20)2+16
y=-x2+x+1
5.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
C
6.河北省赵县的赵州桥的桥拱是抛物线形,水面宽为30米,水面离桥顶的高度是9米,建立如图所示的直角坐标系,你能求出桥拱所在抛物线的函数关系式吗
解:设这条抛物线表示的二次函数为y=ax2.
由已知条件可知抛物线经过点(15,-9),可得-9=a×152
解得,a=-
因此,桥拱所在抛物线的函数关系式为:y=-x2
7.如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米
解:如图,建立直角坐标系
则点B的坐标是(0,3.5),点C的坐标是(1.5,3.05)
点A表示运动员投篮球的出手处
设y=ax2+3.5
把C(1.5,3.05)代入y=ax2+3.5得3.05=2.25a+3.5,解得a=-0.2
∴y=-0.2x2+3.5
当x=-2.5时,y=2.25
故运动员出手时的高度为2.25m。
转化
回归
(二次函数的图象和性质)
拱桥问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
实际问题与二次函数
(三) 拱桥问题中的抛物线
第二十二章 二次函数
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.(重点)
2.利用二次函数解决拱桥及运动中的有关问题.(重、难点)
3.能运用二次函数的图象与性质进行决策.
1.函数y=ax2(a≠0)的图象是一条_______,它的顶点坐标是_______,对称轴是_____,当a____时,开口向上,当a____时,开口向下.
2.二次函数解析式的形式有:
①一般式:____________,
②顶点式:_____________,
③交点式:________________.
3.(1)如图所示的抛物线,可以根据顶点所在的位置设为_________,也可以根据抛物线与x轴的交点坐标设为______________.
(2)由A,B两点的横坐标,可以求得线段AB的长
为______.
抛物线
(0,0)
y轴
>0
<0
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
y=ax2+2
y=a(x+2)(x-2)
4
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
解:以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设这条抛物线表示的二次函数为y=ax2.由抛物线经过点(2,-2),可得
-2=a×22,解得,a=-
∴ 这条抛物线表示的二次函数为:y=-x2
当水面下降1m时,水面的纵坐标为-3.
当y=-3时,x=±.
∴当水面下降1m时,水面的宽度为2m.
∴水面的宽度增加了(2-4)m.
你有其它解法吗?
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
解:以离拱顶2m时的水面为x轴,以抛物线的对称轴为y轴建立直角坐标系.
设这条抛物线表示的二次函数为y=ax2+2.由抛物线经过点(2,0),可得
0=a×22+2,解得,a=-
∴ 这条抛物线表示的二次函数为:y=-x2+2
当水面下降1m时,水面的纵坐标为-1.
当y=-1时,x=±.
∴当水面下降1m时,水面的宽度为2m.
∴水面的宽度增加了(2-4)m.
在“拱桥类”问题中,一般知道拱高和拱长,这时可根据抛物线的对称性建立以对称轴为y轴的坐标系,然后根据所建立的坐标系,确定抛物线上一些点的坐标.若顶点在原点上,一般设二次函数的解析式为y=ax2;若顶点不在原点上,一般设二次函数的解析式为y=ax2+k.
步骤:
(1)恰当地建立直角坐标系;
(2)将已知条件转化为点的坐标;
(3)合理地设出所求函数关系式;
(4)代入已知条件或点的坐标求出关系式;
(5)利用关系式求解问题.
例1.如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-0.25x2+4表示.
(1)一辆高5.2m,宽2m的货运卡车能通过该隧道吗
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过
解:(1)建立相应的坐标系.当货运卡车在正中央时,
即对应的x=±1,y=3.75.
∵3.75+2>5.2
∴它能通过该隧道
(2)当隧道内设双行道时,就意味着货运卡车只能走一边,即对应的x=±2,y=3.
∵3+2<5.2
∴它不能通过该隧道.
例2.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管如图做成的立柱,为了计算所需不锈钢立柱的总长度,设计人员测得如图所示的数据.
(1)求该抛物线的解析式;
(2)计算所需不锈钢管的总长度.
解:(1)以0为原点建立直角坐标.
设此抛物线解析式为y=ax(x-2),
依题意得,抛物线顶点坐标为(1,0.5)
∴0.5=a×1×(1-2),解得a=-
∴该抛物线的解析式为y=-x(x-2),即y=-x2+x.
例2.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管如图做成的立柱,为了计算所需不锈钢立柱的总长度,设计人员测得如图所示的数据.
(1)求该抛物线的解析式; y=-x2+x
(2)计算所需不锈钢管的总长度.
解:(2)依题意得:
当x=0.4时,y=0.32
当x=0.8时,y=0.48
当x=1.2时,y=0.48
当x=1.6时,y=0.32
所需不锈钢管的总长度为50×2×(0.32+0.48)=80m.
例3.如图,已知排球场的长度OD为18米,位于球场中线处的球网AB的高度2.24米,一队员站在点0处发球,排球从点0的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点0的水平距离OE为6米时,到达最高点G,以0为原点建立如图所示的平面直角坐标系.
(1)若排球运行的最大高度为2.8米,求排球飞行的高度p(单位:米)与水平距离x(单位:米)之间的函数关系式;
解:(1)由题意知顶点G的坐标为(6,2.8),则设抛物线的解析式为p=a(x-6)2+2.8
∵点C坐标为(0,2),且在抛物线上
∴2=a(0-6)2+2.8,解得a=-.
∴p=-(x-6)2+2.8
例3.如图,已知排球场的长度OD为18米,位于球场中线处的球网AB的高度2.24米,一队员站在点0处发球,排球从点0的正上方2米的C点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点0的水平距离OE为6米时,到达最高点G,以0为原点建立如图所示的平面直角坐标系.
(2)在(1)的条件下,这次所发的球能够过网吗 如果能够过网,是否会出界 请说明理由;
解:(2)当x=9时,p=-×(9-6)2+2.8
=2.6>2.24
当x=18时,p=-×(18-6)2+2.8=-0.4<0
故这次发球可以过网且不出边界
(3)若该队员发球要想过网,又使排球不会出界(排球压线属于没出界),求二次函数中二次项系数的最大值.
解:(3)设抛物线的解析式为p=a(x-6)2+h
将点C(0,2)代入得36a+h=2,即h=2-36a
∴p=a(x-6)2+2-36a
根据题意,不出边界时有
a(18-6)2+2-36a≤0,解得a≤-
要使排球过网,则a(9-6)2+2-36a≥2.24,解得a≤-故二次函数中二次项系数的最大值为-
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在____s后落地.
2.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是____米.
4
4
3.有一个抛物线形桥拱,其最大高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系中(如右图),则此抛物线的解析式为__________________.
4.在一次羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线y=-元2+bx+c的一部分(如图),其中出球点B离地面0点的距离是1m,球落地点A到0点的距离是4m,那么这条抛物线的解析式为_____________.
y=-0.04(x-20)2+16
y=-x2+x+1
5.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
C
6.河北省赵县的赵州桥的桥拱是抛物线形,水面宽为30米,水面离桥顶的高度是9米,建立如图所示的直角坐标系,你能求出桥拱所在抛物线的函数关系式吗
解:设这条抛物线表示的二次函数为y=ax2.
由已知条件可知抛物线经过点(15,-9),可得-9=a×152
解得,a=-
因此,桥拱所在抛物线的函数关系式为:y=-x2
7.如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米
解:如图,建立直角坐标系
则点B的坐标是(0,3.5),点C的坐标是(1.5,3.05)
点A表示运动员投篮球的出手处
设y=ax2+3.5
把C(1.5,3.05)代入y=ax2+3.5得3.05=2.25a+3.5,解得a=-0.2
∴y=-0.2x2+3.5
当x=-2.5时,y=2.25
故运动员出手时的高度为2.25m。
转化
回归
(二次函数的图象和性质)
拱桥问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
