数学人教A版(2019)必修第一册4.2.2指数函数的图象与性质(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.2.2指数函数的图象与性质(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 577.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 08:44:19 | ||
图片预览


文档简介
(共17张PPT)
指数函数的图象和性质
动手实践
y=ax(a>0且a≠1)的代表图象及其一般性质
用描点法作出下列两组函数的图象,然后写出其一些性质:
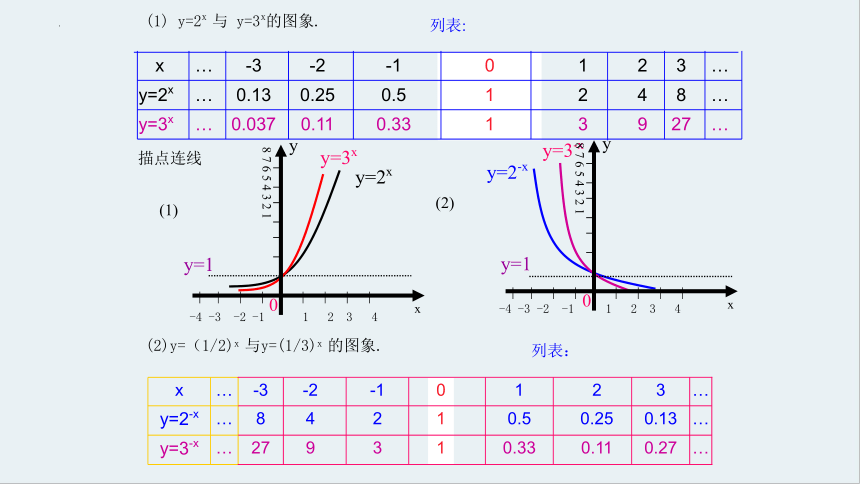
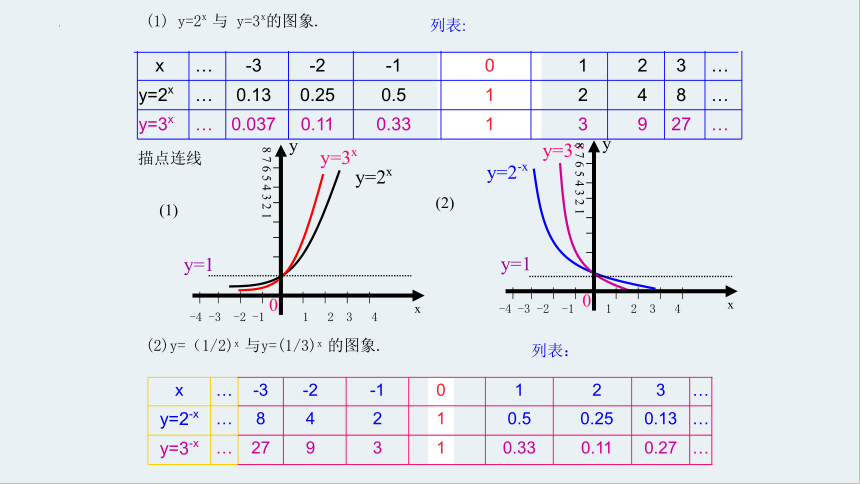
(1) y=2x 与 y=3x ; (a>1)
(2) y=(1/2)x 与 y=(1/3)x . (0…
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
8
4
2
1
0.5
0.25
0.13
…
y=2x
…
3
2
1
0
-1
-2
-3
…
x
(1) y=2x 与 y=3x的图象.
描点连线
y=2x
y=3x
y=2-x
y=3-x
y=1
y=1
…
0.27
0.11
0.33
1
3
9
27
…
y=3-x
…
0.13
0.25
0.5
1
2
4
8
…
y=2-x
…
3
2
1
0
-1
-2
-3
…
x
(2)y=(1/2)x 与y=(1/3)x 的图象.
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(1)
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(2)
列表:
列表:
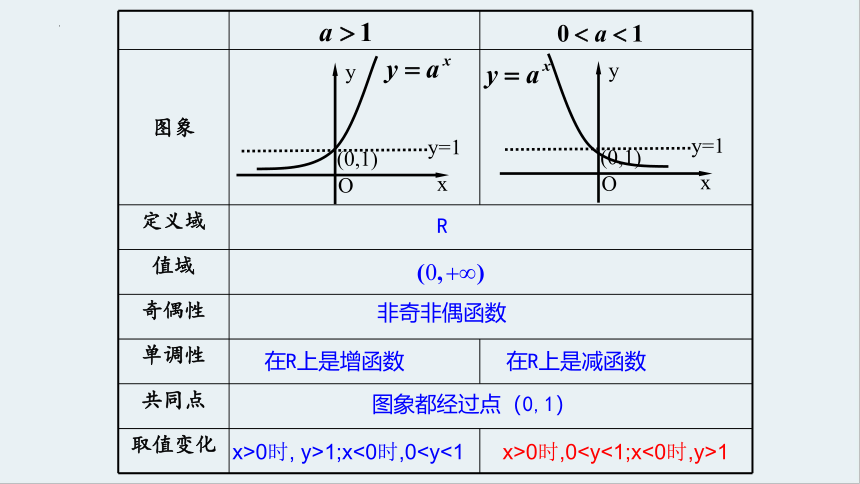
图象
定义域
值域
奇偶性
单调性
共同点
取值变化
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
在R上是增函数
在R上是减函数
R
非奇非偶函数
图象都经过点(0,1)
x>0时, y>1;x<0时,0x>0时,01
…
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
8
4
2
1
0.5
0.25
0.13
…
y=2x
…
3
2
1
0
-1
-2
-3
…
x
(1) y=2x 与 y=3x的图象.
描点连线
y=2x
y=3x
y=2-x
y=3-x
y=1
y=1
…
0.27
0.11
0.33
1
3
9
27
…
y=3-x
…
0.13
0.25
0.5
1
2
4
8
…
y=2-x
…
3
2
1
0
-1
-2
-3
…
x
(2)y=(1/2)x 与y=(1/3)x 的图象.
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(1)
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(2)
列表:
列表:
y=1
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
y=3x
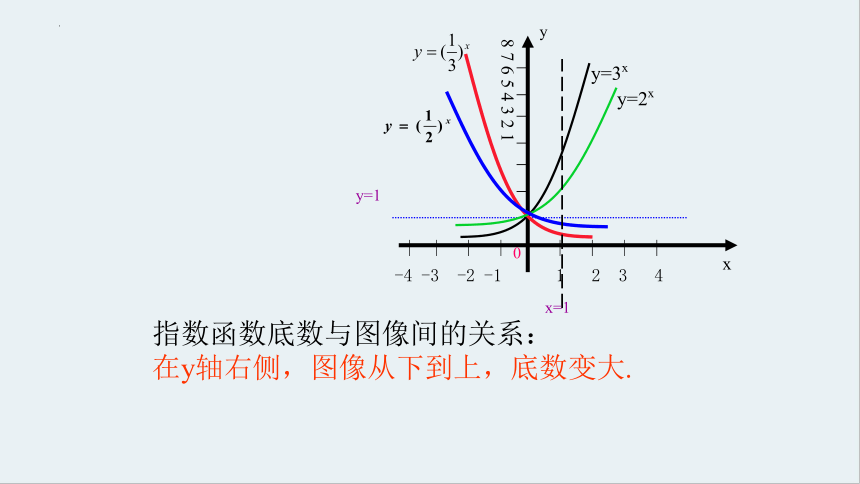
指数函数底数与图像间的关系:
在y轴右侧,图像从下到上,底数变大.
y=2x
x=1
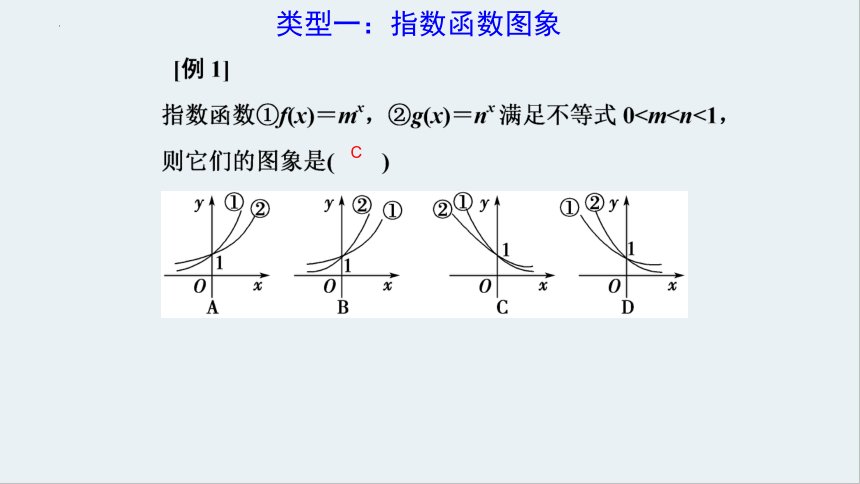
类型一:指数函数图象
C
方法:作直线x=1,即可得到对应的底数的大小关系.
B
课堂练习
1.如图是指数函数f(x)=ax的图象,已知a的值取分别为 ,则相应于曲线C1,C2,C3,C4的选项依次是( )
y=1
(3,4)
D
解简单的指数不等式
《金版》P84
利用指数函数单调性比较大小
点评:比较幂的大小的方法
(1)对于底数相同,但指数不同的幂的大小比较,可以利用指 数函数的单调性来判断,
(2)对于底数不同,指数相同的幂的大小比较,可利用指数函数的图象的变化规律来判断.
(3)对于底数不同且指数不同的幂的大小比较,则应通过中间值来比较.(中间值常为1)
(4)当底数含参数时,要按底数a>1和0 解简单的指数不等式
4. 知实数a, b满足等式 ,下列五个关系式:
①0④b其中不可能成立的关系式有 ( )
A.1个 B.2个 C.3个 D.4个
B
丰收园:
1.本节课学习了那些知识
2.如何记忆函数的性质
3.数形结合的方法记忆
1.比较下列各组数的大小.
作业:(写在作业本上
3.求不等式a2x-7>a4x-1(a>0,且a≠1)中x的取值范围
当a>1时,x的取值范围为(-∞,-3);
当0一、作业:
课本P115页练习1,2,3,
P118的第1到4题及6
写在课本上,星期三检查
课外任务
指数函数的图象和性质
动手实践
y=ax(a>0且a≠1)的代表图象及其一般性质
用描点法作出下列两组函数的图象,然后写出其一些性质:
(1) y=2x 与 y=3x ; (a>1)
(2) y=(1/2)x 与 y=(1/3)x . (0
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
8
4
2
1
0.5
0.25
0.13
…
y=2x
…
3
2
1
0
-1
-2
-3
…
x
(1) y=2x 与 y=3x的图象.
描点连线
y=2x
y=3x
y=2-x
y=3-x
y=1
y=1
…
0.27
0.11
0.33
1
3
9
27
…
y=3-x
…
0.13
0.25
0.5
1
2
4
8
…
y=2-x
…
3
2
1
0
-1
-2
-3
…
x
(2)y=(1/2)x 与y=(1/3)x 的图象.
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(1)
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(2)
列表:
列表:
图象
定义域
值域
奇偶性
单调性
共同点
取值变化
O
x
y
(0,1)
y=1
O
x
y
(0,1)
y=1
在R上是增函数
在R上是减函数
R
非奇非偶函数
图象都经过点(0,1)
x>0时, y>1;x<0时,0
…
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
8
4
2
1
0.5
0.25
0.13
…
y=2x
…
3
2
1
0
-1
-2
-3
…
x
(1) y=2x 与 y=3x的图象.
描点连线
y=2x
y=3x
y=2-x
y=3-x
y=1
y=1
…
0.27
0.11
0.33
1
3
9
27
…
y=3-x
…
0.13
0.25
0.5
1
2
4
8
…
y=2-x
…
3
2
1
0
-1
-2
-3
…
x
(2)y=(1/2)x 与y=(1/3)x 的图象.
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(1)
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
(2)
列表:
列表:
y=1
y
8 7 6 5 4 3 2 1
0
-4 -3 -2 -1 1 2 3 4
x
y=3x
指数函数底数与图像间的关系:
在y轴右侧,图像从下到上,底数变大.
y=2x
x=1
类型一:指数函数图象
C
方法:作直线x=1,即可得到对应的底数的大小关系.
B
课堂练习
1.如图是指数函数f(x)=ax的图象,已知a的值取分别为 ,则相应于曲线C1,C2,C3,C4的选项依次是( )
y=1
(3,4)
D
解简单的指数不等式
《金版》P84
利用指数函数单调性比较大小
点评:比较幂的大小的方法
(1)对于底数相同,但指数不同的幂的大小比较,可以利用指 数函数的单调性来判断,
(2)对于底数不同,指数相同的幂的大小比较,可利用指数函数的图象的变化规律来判断.
(3)对于底数不同且指数不同的幂的大小比较,则应通过中间值来比较.(中间值常为1)
(4)当底数含参数时,要按底数a>1和0
4. 知实数a, b满足等式 ,下列五个关系式:
①0
A.1个 B.2个 C.3个 D.4个
B
丰收园:
1.本节课学习了那些知识
2.如何记忆函数的性质
3.数形结合的方法记忆
1.比较下列各组数的大小.
作业:(写在作业本上
3.求不等式a2x-7>a4x-1(a>0,且a≠1)中x的取值范围
当a>1时,x的取值范围为(-∞,-3);
当0
课本P115页练习1,2,3,
P118的第1到4题及6
写在课本上,星期三检查
课外任务
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
