第11章 三角形 单元同步检测试题(含答案)
文档属性
| 名称 | 第11章 三角形 单元同步检测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 335.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十一章《三角形》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
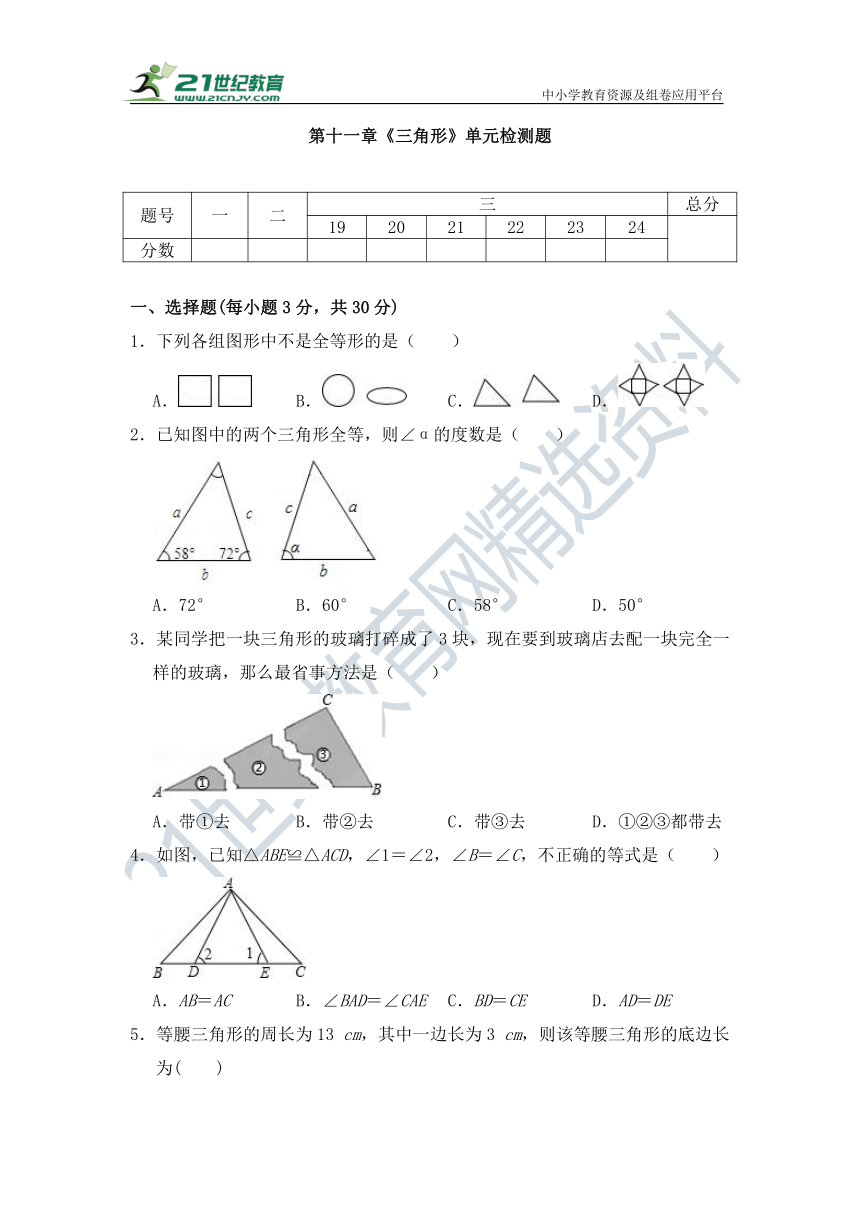
1.下列各组图形中不是全等形的是( )
A. B. C. D.
2.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC B.∠BAD=∠CAE C.BD=CE D.AD=DE
5.等腰三角形的周长为13 cm,其中一边长为3 cm,则该等腰三角形的底边长为( )
A.7 cm B.3 cm C.9 cm D.5 cm
6.下列说法中正确的是 ( )
A.三角形的外角大于任何一个内角
B.三角形的内角和小于外角和
C.三角形的外角和小于四边形的外角和
D.三角形的一个外角等于两个两个内角的和.
7.一个多边形除一个内角外,其余各内角之和是,则这个内角的度数为.
A. B. C. D.
8.锐角三角形ABC中,,且最大内角比最小内角大,则的取值范围是
A. A B. A C. A D. A
9.如图,AD是的角平分钱,,垂足为若,,则的度数为
A. B. C. D.
10.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC; ②∠BDC=∠BAC;③∠ADC=90°﹣∠ABD; ④BD平分∠ADC.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 三角形.
12.一个三角形中,最少有 个锐角.
13.三角形中最大角α的范围为 ,最小角β的范围是 .
14.在△ABC中,∠A=∠B=∠C,则∠A= ,∠B= ,∠C= .此三角形为 三角形.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于 .
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为 .
17. 如图所示,在△ABC中,∠A=36°,E是BC延长线上一点,∠DBE=∠ABE,∠DCE=∠ACE,则∠D的度数为________.
18. 如图,在△ABC中,点D在BC的延长线上,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2019BC和∠A2019CD的平分线交于点A2020,则∠A2020=________°.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,∠C=70°,∠DAE=15°,求∠B的度数.
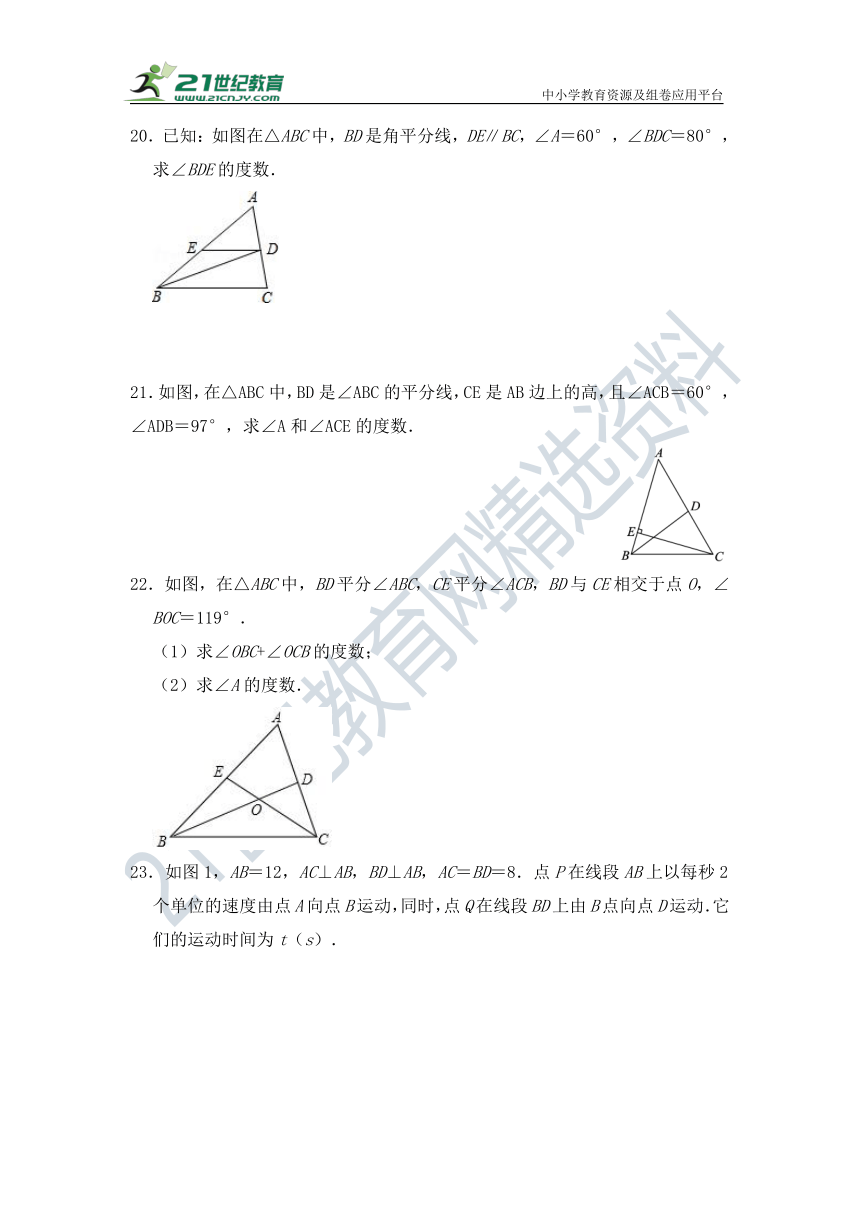
20.已知:如图在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=80°,求∠BDE的度数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE相交于点O,∠BOC=119°.
(1)求∠OBC+∠OCB的度数;
(2)求∠A的度数.
23.如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8.点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动.它们的运动时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=2时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
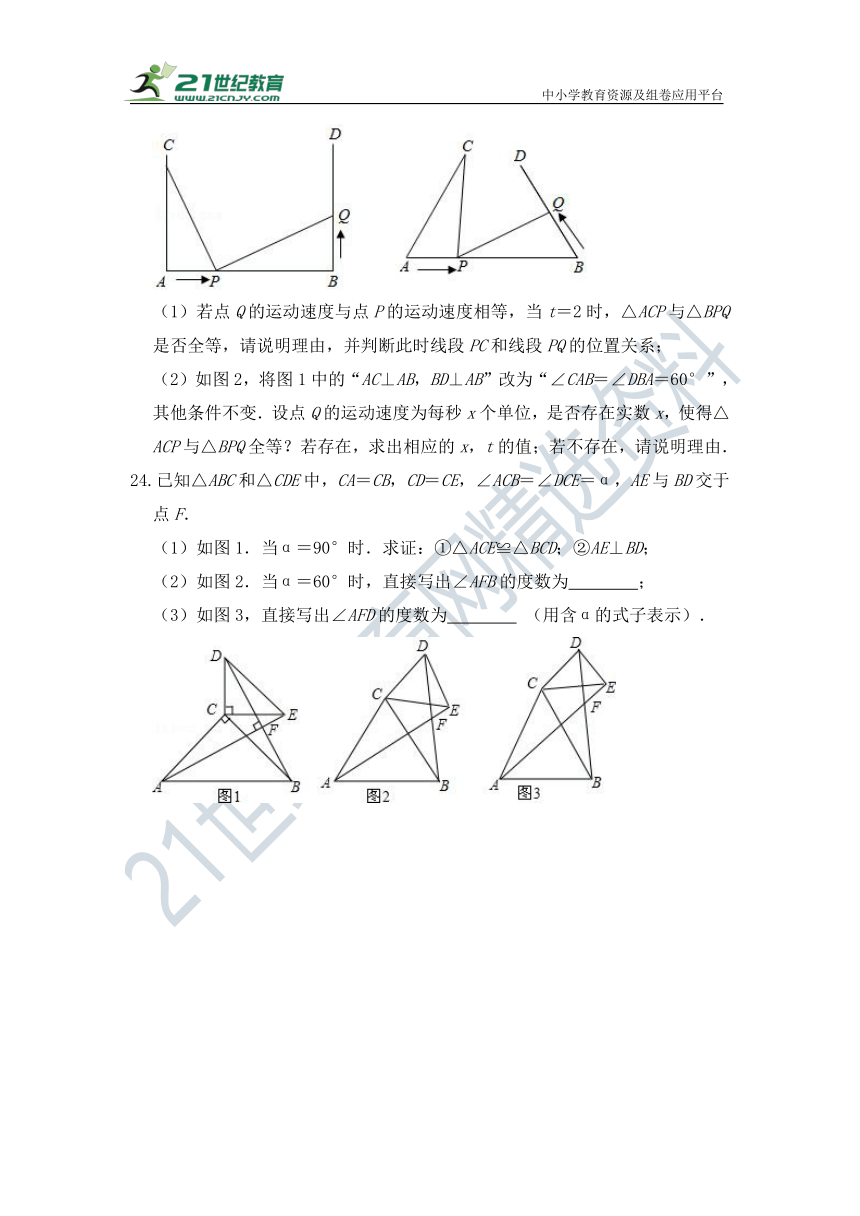
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为每秒x个单位,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由.
24.已知△ABC和△CDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.
(1)如图1.当α=90°时.求证:①△ACE≌△BCD;②AE⊥BD;
(2)如图2.当α=60°时,直接写出∠AFB的度数为 ;
(3)如图3,直接写出∠AFD的度数为 (用含α的式子表示).
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C D B B C D B B
二、填空题
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 钝角 三角形.
【分析】设∠B为x,则∠A=2x,∠C=3x+12,根据三角形的内角和定理可列出方程,从而解出即可得出答案.
【解答】解:设∠B为x,则∠A=2x,∠C=3x+12,
由题意得:x+2x+3x+12=180°,
解得:x=28°,2x=56°,3x+12=96°,
即三角形为钝角三角形.
故答案为:钝角.
12.一个三角形中,最少有 2 个锐角.
【分析】根据三角形的内角和等于180°,三个角中最多有一个直角或钝角,所以最少有两个锐角.
【解答】解:∵三角形的内角和等于180°,
∴三角形最多有一个直角或钝角,剩下的两个为锐角.
∴一个三角形中,最少有2个锐角.
故答案为:2.
13.三角形中最大角α的范围为 60°≤α<180° ,最小角β的范围是 0°<β≤60° .
【分析】利用三角形内角和定理,用反证法来说明最大最小角的范围.
【解答】解:根据三角形内角和定理知,内角和为180°,则最大角不<60°;若最大角<60°,则三个内角的和就<了180°,这与内定理矛盾;
同样,最小应不>60°;若最小角>了60°,则三个内角的和就>了180°,这与内角和定理也矛盾.
故:三角形中最大角α的范围为60°≤α<180°,最小角β的范围是0°<β≤60°.
14.在△ABC中,∠A=∠B=∠C,则∠A= 30° ,∠B= 60° ,∠C= 90° .此三角形为 直角 三角形.
【分析】由题意可得∠B=2∠A,∠C=3∠A,根据三角形的内角和定理求出∠A,即可得∠B,∠C的度数,即可求解.
【解答】解:∵,∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴6∠A=180°,
∴∠A=30°,
∴∠B=2∠A=60°,∠C=3∠A=90°,
∴此三角形为直角三角形.
故答案为:30°,60°,90°,直角.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于 50° .
【分析】设∠A=3k,∠B=5k,∠C=10k,由三角形内角和为180度可求出k,从而求出∠B.
【解答】解:由题意可设∠A=3k,∠B=5k,∠C=10k,
则3k+5k+10k=180°,
∴k=10°,
∴∠B=50°.
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为 90° .
【分析】首先求出∠B=60°,不妨设∠A=30°,则∠C=180°﹣30°﹣60°=90°,即可即可解决问题.
【解答】解:∵∠A+∠C=2∠B,
又∵∠A+∠B+∠C=180°,
∴3∠B=180°,
∴∠B=60°,
设∠A=30°,则∠C=180°﹣30°﹣60°=90°,
∴△ABC中,最大的角为90°.
故答案为:90°.
17. 【答案】24° [解析] ∠D=∠DCE-∠DBE=∠ACE-∠ABE=(∠ACE-∠ABE)=∠A=×36°=24°.
18. 【答案】()
三、解答题
19.解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣70°=20°,
∵∠DAE=15°,
∴∠CAE=∠DAE+∠CAD=15°+20°=35°,
∵AE平分∠BAC,
∴∠BAC=2∠EAC=70°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣70°﹣70°=40°.
20.已知:如图在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=80°,求∠BDE的度数.
【分析】根据∠A=60°,∠BDC=80°,可以得到∠ABD的度数,再根据BD是角平分线,DE∥BC,即可得到∠BDE的度数.
【解答】解:∵∠A=60°,∠BDC=80°,∠BDC=∠A+∠ABD,
∴∠ABD=20°,
∵BD是角平分线,
∴∠ABD=∠DBC=20°,
∵DE∥BC,
∴∠EDB=∠DBC=20°,
即∠BDE的度数是20°.
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.解:(1)∵∠BOC=119°
∴△BCO中,∠OBC+∠OCB=180°﹣∠BOC=61°;
(2)∵BD平分∠ABC,CE平分∠ACB,
∴∠ABC+∠ACB=2∠OBC+2∠OCB=2(∠OBC+∠OCB)=122°,
∴△ABC中,∠A=180°﹣122°=58°.
23.解:(1)结论:△ACP与△BPQ全等.
理由如下:当t=2时,AP=BQ=2×2=4,
则BP=AB﹣AP=12﹣4=8,
∴BP=AC,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
,
∴△ACP≌△BPQ(SAS);
结论:PC⊥PQ.
证明:∵△ACP≌△BPQ,
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
∴,
解得
;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得
;
综上所述,当或时,
使得△ACP与△BPQ全等.
24.
【解答】证明:(1)∵∠ACB=∠DCE=90°,
∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE=∠BCD,
又∵△ABC和△ECD都是等腰直角三角形
∴AC=BC,EC=DC,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=90°,
∴∠CBD+∠EAB+∠ABC=90°,
∴∠AFB=90°,
∴AE⊥BD;
(2)∵∠ACB=∠DCE=60°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=120°,
∴∠CBD+∠EAB+∠ABC=120°,
∴∠AFB=∠ACB=60°;
故答案为:60°;
(3))∵∠ACB=∠DCE=α,
∴∠ACB+∠BCE=∠DCE+∠BCE 即∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=180°﹣α,
∴∠CBD+∠EAB+∠ABC=180°﹣α∴∠AFB=∠ACB=α,
∴∠AFD=180°﹣α.
故答案为:180°﹣α.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第十一章《三角形》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.下列各组图形中不是全等形的是( )
A. B. C. D.
2.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC B.∠BAD=∠CAE C.BD=CE D.AD=DE
5.等腰三角形的周长为13 cm,其中一边长为3 cm,则该等腰三角形的底边长为( )
A.7 cm B.3 cm C.9 cm D.5 cm
6.下列说法中正确的是 ( )
A.三角形的外角大于任何一个内角
B.三角形的内角和小于外角和
C.三角形的外角和小于四边形的外角和
D.三角形的一个外角等于两个两个内角的和.
7.一个多边形除一个内角外,其余各内角之和是,则这个内角的度数为.
A. B. C. D.
8.锐角三角形ABC中,,且最大内角比最小内角大,则的取值范围是
A. A B. A C. A D. A
9.如图,AD是的角平分钱,,垂足为若,,则的度数为
A. B. C. D.
10.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC; ②∠BDC=∠BAC;③∠ADC=90°﹣∠ABD; ④BD平分∠ADC.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 三角形.
12.一个三角形中,最少有 个锐角.
13.三角形中最大角α的范围为 ,最小角β的范围是 .
14.在△ABC中,∠A=∠B=∠C,则∠A= ,∠B= ,∠C= .此三角形为 三角形.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于 .
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为 .
17. 如图所示,在△ABC中,∠A=36°,E是BC延长线上一点,∠DBE=∠ABE,∠DCE=∠ACE,则∠D的度数为________.
18. 如图,在△ABC中,点D在BC的延长线上,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2019BC和∠A2019CD的平分线交于点A2020,则∠A2020=________°.
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,∠C=70°,∠DAE=15°,求∠B的度数.
20.已知:如图在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=80°,求∠BDE的度数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE相交于点O,∠BOC=119°.
(1)求∠OBC+∠OCB的度数;
(2)求∠A的度数.
23.如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8.点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动.它们的运动时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=2时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为每秒x个单位,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由.
24.已知△ABC和△CDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.
(1)如图1.当α=90°时.求证:①△ACE≌△BCD;②AE⊥BD;
(2)如图2.当α=60°时,直接写出∠AFB的度数为 ;
(3)如图3,直接写出∠AFD的度数为 (用含α的式子表示).
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C D B B C D B B
二、填空题
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 钝角 三角形.
【分析】设∠B为x,则∠A=2x,∠C=3x+12,根据三角形的内角和定理可列出方程,从而解出即可得出答案.
【解答】解:设∠B为x,则∠A=2x,∠C=3x+12,
由题意得:x+2x+3x+12=180°,
解得:x=28°,2x=56°,3x+12=96°,
即三角形为钝角三角形.
故答案为:钝角.
12.一个三角形中,最少有 2 个锐角.
【分析】根据三角形的内角和等于180°,三个角中最多有一个直角或钝角,所以最少有两个锐角.
【解答】解:∵三角形的内角和等于180°,
∴三角形最多有一个直角或钝角,剩下的两个为锐角.
∴一个三角形中,最少有2个锐角.
故答案为:2.
13.三角形中最大角α的范围为 60°≤α<180° ,最小角β的范围是 0°<β≤60° .
【分析】利用三角形内角和定理,用反证法来说明最大最小角的范围.
【解答】解:根据三角形内角和定理知,内角和为180°,则最大角不<60°;若最大角<60°,则三个内角的和就<了180°,这与内定理矛盾;
同样,最小应不>60°;若最小角>了60°,则三个内角的和就>了180°,这与内角和定理也矛盾.
故:三角形中最大角α的范围为60°≤α<180°,最小角β的范围是0°<β≤60°.
14.在△ABC中,∠A=∠B=∠C,则∠A= 30° ,∠B= 60° ,∠C= 90° .此三角形为 直角 三角形.
【分析】由题意可得∠B=2∠A,∠C=3∠A,根据三角形的内角和定理求出∠A,即可得∠B,∠C的度数,即可求解.
【解答】解:∵,∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴6∠A=180°,
∴∠A=30°,
∴∠B=2∠A=60°,∠C=3∠A=90°,
∴此三角形为直角三角形.
故答案为:30°,60°,90°,直角.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于 50° .
【分析】设∠A=3k,∠B=5k,∠C=10k,由三角形内角和为180度可求出k,从而求出∠B.
【解答】解:由题意可设∠A=3k,∠B=5k,∠C=10k,
则3k+5k+10k=180°,
∴k=10°,
∴∠B=50°.
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为 90° .
【分析】首先求出∠B=60°,不妨设∠A=30°,则∠C=180°﹣30°﹣60°=90°,即可即可解决问题.
【解答】解:∵∠A+∠C=2∠B,
又∵∠A+∠B+∠C=180°,
∴3∠B=180°,
∴∠B=60°,
设∠A=30°,则∠C=180°﹣30°﹣60°=90°,
∴△ABC中,最大的角为90°.
故答案为:90°.
17. 【答案】24° [解析] ∠D=∠DCE-∠DBE=∠ACE-∠ABE=(∠ACE-∠ABE)=∠A=×36°=24°.
18. 【答案】()
三、解答题
19.解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣70°=20°,
∵∠DAE=15°,
∴∠CAE=∠DAE+∠CAD=15°+20°=35°,
∵AE平分∠BAC,
∴∠BAC=2∠EAC=70°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣70°﹣70°=40°.
20.已知:如图在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=80°,求∠BDE的度数.
【分析】根据∠A=60°,∠BDC=80°,可以得到∠ABD的度数,再根据BD是角平分线,DE∥BC,即可得到∠BDE的度数.
【解答】解:∵∠A=60°,∠BDC=80°,∠BDC=∠A+∠ABD,
∴∠ABD=20°,
∵BD是角平分线,
∴∠ABD=∠DBC=20°,
∵DE∥BC,
∴∠EDB=∠DBC=20°,
即∠BDE的度数是20°.
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.解:(1)∵∠BOC=119°
∴△BCO中,∠OBC+∠OCB=180°﹣∠BOC=61°;
(2)∵BD平分∠ABC,CE平分∠ACB,
∴∠ABC+∠ACB=2∠OBC+2∠OCB=2(∠OBC+∠OCB)=122°,
∴△ABC中,∠A=180°﹣122°=58°.
23.解:(1)结论:△ACP与△BPQ全等.
理由如下:当t=2时,AP=BQ=2×2=4,
则BP=AB﹣AP=12﹣4=8,
∴BP=AC,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
,
∴△ACP≌△BPQ(SAS);
结论:PC⊥PQ.
证明:∵△ACP≌△BPQ,
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
∴,
解得
;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得
;
综上所述,当或时,
使得△ACP与△BPQ全等.
24.
【解答】证明:(1)∵∠ACB=∠DCE=90°,
∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE=∠BCD,
又∵△ABC和△ECD都是等腰直角三角形
∴AC=BC,EC=DC,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=90°,
∴∠CBD+∠EAB+∠ABC=90°,
∴∠AFB=90°,
∴AE⊥BD;
(2)∵∠ACB=∠DCE=60°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=120°,
∴∠CBD+∠EAB+∠ABC=120°,
∴∠AFB=∠ACB=60°;
故答案为:60°;
(3))∵∠ACB=∠DCE=α,
∴∠ACB+∠BCE=∠DCE+∠BCE 即∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠CAE+∠EAB+∠ABC=180°﹣α,
∴∠CBD+∠EAB+∠ABC=180°﹣α∴∠AFB=∠ACB=α,
∴∠AFD=180°﹣α.
故答案为:180°﹣α.
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
