有理数的乘法(1)[上学期]
文档属性
| 名称 | 有理数的乘法(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-19 00:00:00 | ||
图片预览


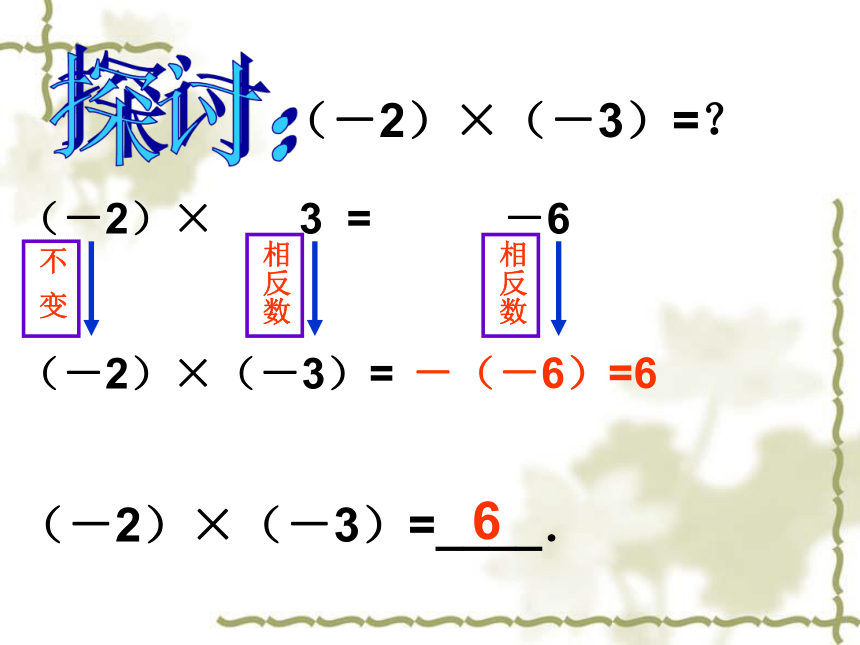


文档简介
课件14张PPT。有理数的乘法(1)蓬街私立中学 周学霄算一算⑴ 2× ⑵ 0 ×7.5
⑶ 1×56 ⑷ 2×3
⑸ (-2)+(-2)+(-2)=-6式子(-2)+(-2)+(-2)
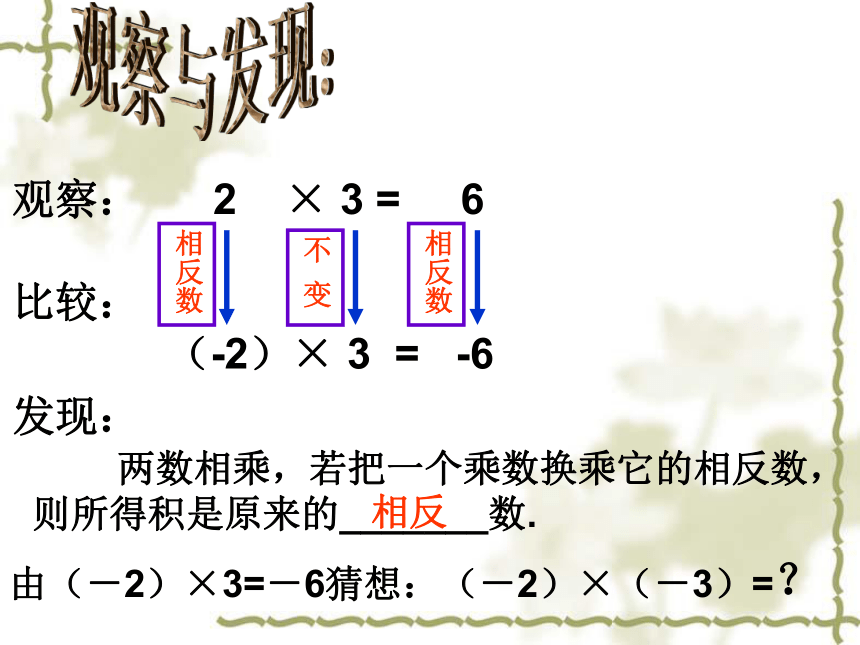
能写成乘法的形式吗?想一想,做一做:(-2)×4.如何计算(-2)×3呢?由(-2)+(-2)+(-2)=-6.可知:(-2)×3=-6.观察与发现:观察: 2 × 3 = 6
比较:
(-2)× 3 = -6相反数相反数不 变发现:由(-2)×3=-6猜想:(-2)×(-3)=? 两数相乘,若把一个乘数换乘它的相反数,则所得积是原来的_______数.相反(-2)× 3 = -6
(-2)×(-3)=-(-6)=6 探讨:(-2)×(-3)=?不 变相反数相反数(-2)×(-3)=____.6 2 ×3 = 6 ⑴
(-2)×3 =-6 ⑵
(-2)×(-3)= 6 ⑶观察并填空:正数×正数=___数
正数×负数=___数
负数×负数=___数乘积的绝对值等于各乘数的绝对值的_____.正负正乘积归纳:有理数的乘法法则: 两数相乘,同号得___;异号得___;并把____相乘.正负绝对值应用:例1 计算:
⑴(-3)×9 ⑵(-5)×
⑶(-7)×1 ⑷(-4)×(-1)应用法则:有理数相乘,先确定积的_____;再确定积的_______.绝对值符号看谁做得又对又快:⑴6×(-9); ⑵(-4)×6;
⑶(-6)×(-1);⑷(-6)×9;
⑸ × ; ⑹ × .通过观察例1并结合小学学习的乘法法则讨论:⑴一个数同1相乘;得_______.
⑵一个数同-1相乘;得_________.
⑶一个数同0相乘;得_______.
⑷乘积是1的两个数是________.合作与交流原数原数相反数0互为倒数例2:用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1Km气温的变化量为-6oC,攀登3Km后,气温有什么变化?1.写出下列各数的倒数:
1,-1, , ,5, -5, , .动手又动脑2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗?课堂小结有理数的乘法法则: 两数相乘,同号得___;异号得___;并把_______相乘.有理数相乘,先确定积的_____;再确定积的______.符号绝对值绝对值正负GOODBYE!
⑶ 1×56 ⑷ 2×3
⑸ (-2)+(-2)+(-2)=-6式子(-2)+(-2)+(-2)
能写成乘法的形式吗?想一想,做一做:(-2)×4.如何计算(-2)×3呢?由(-2)+(-2)+(-2)=-6.可知:(-2)×3=-6.观察与发现:观察: 2 × 3 = 6
比较:
(-2)× 3 = -6相反数相反数不 变发现:由(-2)×3=-6猜想:(-2)×(-3)=? 两数相乘,若把一个乘数换乘它的相反数,则所得积是原来的_______数.相反(-2)× 3 = -6
(-2)×(-3)=-(-6)=6 探讨:(-2)×(-3)=?不 变相反数相反数(-2)×(-3)=____.6 2 ×3 = 6 ⑴
(-2)×3 =-6 ⑵
(-2)×(-3)= 6 ⑶观察并填空:正数×正数=___数
正数×负数=___数
负数×负数=___数乘积的绝对值等于各乘数的绝对值的_____.正负正乘积归纳:有理数的乘法法则: 两数相乘,同号得___;异号得___;并把____相乘.正负绝对值应用:例1 计算:
⑴(-3)×9 ⑵(-5)×
⑶(-7)×1 ⑷(-4)×(-1)应用法则:有理数相乘,先确定积的_____;再确定积的_______.绝对值符号看谁做得又对又快:⑴6×(-9); ⑵(-4)×6;
⑶(-6)×(-1);⑷(-6)×9;
⑸ × ; ⑹ × .通过观察例1并结合小学学习的乘法法则讨论:⑴一个数同1相乘;得_______.
⑵一个数同-1相乘;得_________.
⑶一个数同0相乘;得_______.
⑷乘积是1的两个数是________.合作与交流原数原数相反数0互为倒数例2:用正数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1Km气温的变化量为-6oC,攀登3Km后,气温有什么变化?1.写出下列各数的倒数:
1,-1, , ,5, -5, , .动手又动脑2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗?课堂小结有理数的乘法法则: 两数相乘,同号得___;异号得___;并把_______相乘.有理数相乘,先确定积的_____;再确定积的______.符号绝对值绝对值正负GOODBYE!
