有理数的大小比较[上学期]
文档属性
| 名称 | 有理数的大小比较[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 531.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-25 00:00:00 | ||
图片预览





文档简介
课件12张PPT。郁文中学1.2.4 绝对值与有理数的大小比较教学目标:
1.掌握有理数的大小比较法则,会比较两个或多个有理数的大小.
2.使学生对有理数有进一步的认识.
重点:有理数的大小比较法则.
难点:两个负数的大小比较.
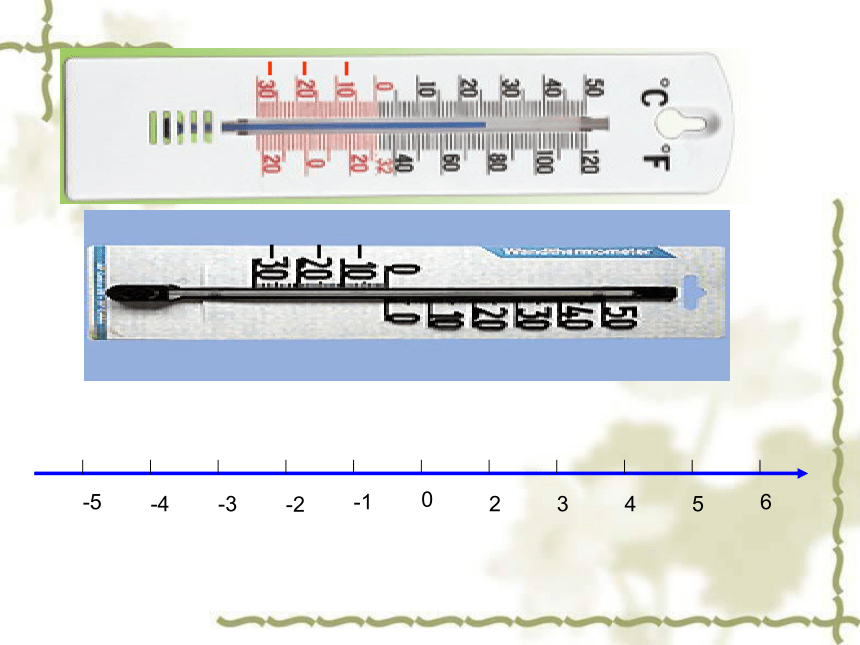
14个温度从底到高的排列为:
-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,我们已经知道两个正数之间是怎样比较大小的,
例如:0<1,1<2.2<3,等等那么任意两个有理数怎么比较大小呢?
例如:-4与-3,-3与-2,-2与-1
-1与0 等等小大数学中规定:在数轴上表示有理数,他们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.练习:
-5 -6 ,-3 -4 ,-9 -6 ,
-5 -2 ,-8 -15
-99 -69,-1 0, -4 2等等>>><<<<<数学中规定:在数轴上表示有理数,他们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.1.正数大于0,0大于负数,正数大于负数;
2.两个负数,绝对值大的反而小.绝对值越来越大
小结论但结果越来越小书P16思考
前面对温度由底到高的排列与上述有理数大小的规定一致吗?例:比较大小
1.-(-1)和-(+2);2. 解:(1) 先化简,
-(-1)=
-(+2)=
因为1>-2(正数大于负数)
所以-(-1) > -(+2)解:这是两个负数比较大小,要考虑它们 的绝对值.
因为|-(8/21)| =8/ 21
| -(3/7) | = 3/7
3/7 = 9/21
所以 -(8/21)| < | -(3/7) |
即 -(8/21) > -(3/7)1-2作业:P18 T4 T5比较有理数的大小可分为3种情况:
1.
2.
3.小结:正书负数正数与负数
2.使学生对有理数有进一步的认识.
重点:有理数的大小比较法则.
难点:两个负数的大小比较.
14个温度从底到高的排列为:
-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,我们已经知道两个正数之间是怎样比较大小的,
例如:0<1,1<2.2<3,等等那么任意两个有理数怎么比较大小呢?
例如:-4与-3,-3与-2,-2与-1
-1与0 等等小大数学中规定:在数轴上表示有理数,他们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.练习:
-5 -6 ,-3 -4 ,-9 -6 ,
-5 -2 ,-8 -15
-99 -69,-1 0, -4 2等等>>><<<<<数学中规定:在数轴上表示有理数,他们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.1.正数大于0,0大于负数,正数大于负数;
2.两个负数,绝对值大的反而小.绝对值越来越大
小结论但结果越来越小书P16思考
前面对温度由底到高的排列与上述有理数大小的规定一致吗?例:比较大小
1.-(-1)和-(+2);2. 解:(1) 先化简,
-(-1)=
-(+2)=
因为1>-2(正数大于负数)
所以-(-1) > -(+2)解:这是两个负数比较大小,要考虑它们 的绝对值.
因为|-(8/21)| =8/ 21
| -(3/7) | = 3/7
3/7 = 9/21
所以 -(8/21)| < | -(3/7) |
即 -(8/21) > -(3/7)1-2作业:P18 T4 T5比较有理数的大小可分为3种情况:
1.
2.
3.小结:正书负数正数与负数
