人教版七年级上册1.2.3 相反数课件(共20张PPT)
文档属性
| 名称 | 人教版七年级上册1.2.3 相反数课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 20:03:42 | ||
图片预览







文档简介
(共20张PPT)
1.2.3 相反数
2
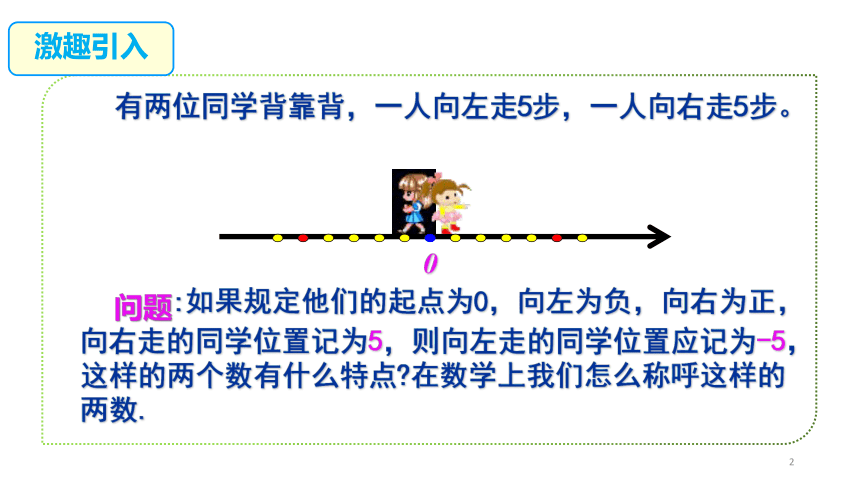
有两位同学背靠背,一人向左走5步,一人向右走5步。
问题:如果规定他们的起点为0,向左为负,向右为正,向右走的同学位置记为5,则向左走的同学位置应记为-5,这样的两个数有什么特点 在数学上我们怎么称呼这样的两数.
0
激趣引入
1.理解相反数的概念,掌握相反数的表示方法,能够准确写出任意数的相反数,对化简符号能正确应用.(重点)
2.熟练负数的相反数的表示方法及化简.(难点)
1、画数轴,在数轴上表示出以下各点:
2,-3,2.5,-2.5,-2,3
2、观察所画的数轴及表示的点回答下列问题:
(1)3与-3分别在原点的 和 。它们到原点的距离为: 。
(2)数轴上与原点距离是2 的点有 个,这些点表示的数是 。
(3)数轴上与原点距离是5 的点有 个,这些点表示的数是 。
动手做
一般地,设a是一个正数,数轴上与原点的距离是a 的点有 个,它们分别在原点的 ,表示 ,我们说这两点关于 。
注意:到原点的距离相等。
两
左侧和右侧
-a和a
原点对称
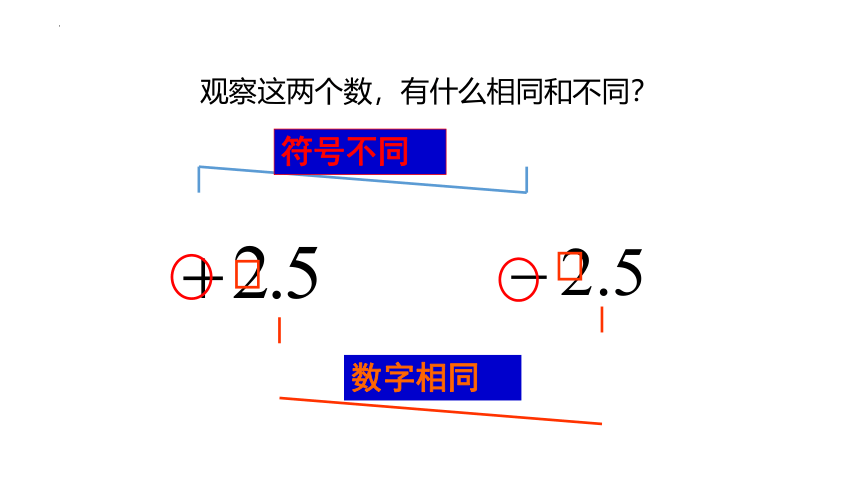
观察这两个数,有什么相同和不同?
数字相同
符号不同
像-2和2,3和-3,-2.5和2.5这样,只有符号不同的两个数叫做互为相反数。
例如:8的相反数是-8,7的相反数是-7。
5的相反数是 .
由此可知,求一个数的相反数就是在这个数的
前面添上“-”号。
一般地,a的相反数是 .
-a
a
-a的相反数是 .
a和-a互为相反数.
???
0的相反数是??(从数轴上考虑)
0的相反数是0。
一个正数的相反数是一个 。
一个负数的相反数是一个 。
负数
正数
一个数的相反数是它本身的数是: .
0
想一想
数轴上表示相反数的两个点和原点有什么关系?
在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等。
例1:求3,-4.5, 的相反数
例2:-1.6是 的相反数
的相反数是0.3
例3:判断
1.符号不同的两个数是相反数。
2.0没有相反数
3.负数的相反数是正数
例4.一个数的相反数比它本身大,则这个数一定是 ( )
A、正数 B、负数 C、0 D、负数和0
通过上面的练习,你知道怎么去表示一个数的相反数吗?比如3在前面添个“-”就变成了它的相反数-3
在一个数的前面添个“-”号,就表示那个数的相反数
例如:-(+4)=-4 -(-4)=4 -(+5.5)=-5.5
在一个数的前面添个“+”号,就表示那个数的本身
如:+(-4)=-4 +(+12)=12
在这,我们对这些符号的化简要求,先读后化
比如-(+4)读作+4的相反数,它等于-4,-(-4)读作-4的相反数,它等于4
+(-4)读作-4的本身,它等于-4,+(+12)读作+12的本身,它等于12
例5.化简下列各数。(先读后写)
(1)-(+10) (2)+(-0.15)
(3)+(+3) (4)-(-12)
你从刚才化简过程中,结果与符号之间有什么关系吗?
两个符号的化简:负负得正,正正得正,正负得负,负正得负。
方法:当负号的个数是奇数个时,结果就为负。
当负号的个数是偶数个时,结果就为正。
(5)-[-(+10)] (6)+[-(-0.15)]
(7)-[+(+3)]
如果是多重符号化简,又应该怎么去化简呢?
-{-[+(-7.5)]}=
例6.下列几对数中互为相反数的对是 ( )
A、-(-8)和-(+8) B、-(+8)和+(+8)
C、-(-8)和-(+8)
例7.5的相反数是 ,a的相反数是 , -a的相反数是 ,a-b的相反数是 ,a+b的相反数是 。
课堂练习
1.-1.6是____的相反数,___的相反数是0.3.
2.下列几对数中互为相反数的一对为( ).
A. 和 B. 与 C. 与
3.5的相反数是____; 的相反数是___; 的相 反数是____.
4.若 ,则 ;
若 ,则 .
5.若 是负数,则 是 ___数;若 是负数,则 是______数.
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
0
思考题:
数轴上,若点 A和点B分别表示互为相反数的两个数,并且这两点的距离是10 ,则这两个点所表示的数分别是_____ 和______ 。
10
课堂小结
本节课学习了以下内容:
1.相反数的概念:只有符号不同的两个数,我们说其中一个是另一个的相反数.
2. 表示求 的相反数.
3.如果a和b互为相反数,则有a+b=_____,且在数轴上表示a和b的两个点——————。
1.2.3 相反数
2
有两位同学背靠背,一人向左走5步,一人向右走5步。
问题:如果规定他们的起点为0,向左为负,向右为正,向右走的同学位置记为5,则向左走的同学位置应记为-5,这样的两个数有什么特点 在数学上我们怎么称呼这样的两数.
0
激趣引入
1.理解相反数的概念,掌握相反数的表示方法,能够准确写出任意数的相反数,对化简符号能正确应用.(重点)
2.熟练负数的相反数的表示方法及化简.(难点)
1、画数轴,在数轴上表示出以下各点:
2,-3,2.5,-2.5,-2,3
2、观察所画的数轴及表示的点回答下列问题:
(1)3与-3分别在原点的 和 。它们到原点的距离为: 。
(2)数轴上与原点距离是2 的点有 个,这些点表示的数是 。
(3)数轴上与原点距离是5 的点有 个,这些点表示的数是 。
动手做
一般地,设a是一个正数,数轴上与原点的距离是a 的点有 个,它们分别在原点的 ,表示 ,我们说这两点关于 。
注意:到原点的距离相等。
两
左侧和右侧
-a和a
原点对称
观察这两个数,有什么相同和不同?
数字相同
符号不同
像-2和2,3和-3,-2.5和2.5这样,只有符号不同的两个数叫做互为相反数。
例如:8的相反数是-8,7的相反数是-7。
5的相反数是 .
由此可知,求一个数的相反数就是在这个数的
前面添上“-”号。
一般地,a的相反数是 .
-a
a
-a的相反数是 .
a和-a互为相反数.
???
0的相反数是??(从数轴上考虑)
0的相反数是0。
一个正数的相反数是一个 。
一个负数的相反数是一个 。
负数
正数
一个数的相反数是它本身的数是: .
0
想一想
数轴上表示相反数的两个点和原点有什么关系?
在数轴上表示互为相反数的两个数的点,分别位于原点的两旁,且与原点的距离相等。
例1:求3,-4.5, 的相反数
例2:-1.6是 的相反数
的相反数是0.3
例3:判断
1.符号不同的两个数是相反数。
2.0没有相反数
3.负数的相反数是正数
例4.一个数的相反数比它本身大,则这个数一定是 ( )
A、正数 B、负数 C、0 D、负数和0
通过上面的练习,你知道怎么去表示一个数的相反数吗?比如3在前面添个“-”就变成了它的相反数-3
在一个数的前面添个“-”号,就表示那个数的相反数
例如:-(+4)=-4 -(-4)=4 -(+5.5)=-5.5
在一个数的前面添个“+”号,就表示那个数的本身
如:+(-4)=-4 +(+12)=12
在这,我们对这些符号的化简要求,先读后化
比如-(+4)读作+4的相反数,它等于-4,-(-4)读作-4的相反数,它等于4
+(-4)读作-4的本身,它等于-4,+(+12)读作+12的本身,它等于12
例5.化简下列各数。(先读后写)
(1)-(+10) (2)+(-0.15)
(3)+(+3) (4)-(-12)
你从刚才化简过程中,结果与符号之间有什么关系吗?
两个符号的化简:负负得正,正正得正,正负得负,负正得负。
方法:当负号的个数是奇数个时,结果就为负。
当负号的个数是偶数个时,结果就为正。
(5)-[-(+10)] (6)+[-(-0.15)]
(7)-[+(+3)]
如果是多重符号化简,又应该怎么去化简呢?
-{-[+(-7.5)]}=
例6.下列几对数中互为相反数的对是 ( )
A、-(-8)和-(+8) B、-(+8)和+(+8)
C、-(-8)和-(+8)
例7.5的相反数是 ,a的相反数是 , -a的相反数是 ,a-b的相反数是 ,a+b的相反数是 。
课堂练习
1.-1.6是____的相反数,___的相反数是0.3.
2.下列几对数中互为相反数的一对为( ).
A. 和 B. 与 C. 与
3.5的相反数是____; 的相反数是___; 的相 反数是____.
4.若 ,则 ;
若 ,则 .
5.若 是负数,则 是 ___数;若 是负数,则 是______数.
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
0
思考题:
数轴上,若点 A和点B分别表示互为相反数的两个数,并且这两点的距离是10 ,则这两个点所表示的数分别是_____ 和______ 。
10
课堂小结
本节课学习了以下内容:
1.相反数的概念:只有符号不同的两个数,我们说其中一个是另一个的相反数.
2. 表示求 的相反数.
3.如果a和b互为相反数,则有a+b=_____,且在数轴上表示a和b的两个点——————。
