湖北省武汉市第四十三高级中学2022-2023学年高二上学期9月开学检测数学试题(PDF版含答案)
文档属性
| 名称 | 湖北省武汉市第四十三高级中学2022-2023学年高二上学期9月开学检测数学试题(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 599.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 10:51:12 | ||
图片预览




文档简介
武汉市第四十三高级中学2022-2023学年高二上学期9月开学检测
数学
一、单项选择题:本大题共 8小题,每小题 5分,共 40分,在每小题给出的四个选项中,只有一项是符合
题目要求的.
1.已知复数 z满足 z i i 2 i,则 z的虚部为( )
A. i B. 3i C. 1 D. 3
2.为了研究某种病毒与血型之间的关系,决定从被感染的人群中抽取样本进行调查,这些感染人群中 O型
血、A型血、B型血、AB型血的人数比为 4:3:3:2,现用比例分配的分层随机抽样方法抽取一个样本量为 n的
样本,已知样本中 O型血的人数比 AB型血的人数多 20,则 n ( )
A.100 B.120 C.200 D.240
2 cos2 sin2
3 3 sin 2 .若
cos
,则 sin 2 ( )
4
2 2 1 1A. B. C. D.
3 3 3 3
4.设 x, y R
,向量a x,1 ,b (1, y),c 1, 2 , a c 且 ,b / /c ,则 x y ( )
A.0 B.1 C.2 D.3
5.设 , 是互不重合的平面, l,m, n是互不重合的直线,下列命题中正确的是( )
A.若m , n ,m//n,则 // B.若 , =l,m l,m ,则m
C.若 // ,m ,n ,则m//n D.若m l,n l,m ,n ,则 l
6.在 ABC中,角 A,B,C的对边分别为 a,b,c ,已知三个向量m a, cos
A
,n b, cos
B
, p c, cos
C
共
2 2 2
线,则 ABC的形状为( )
A.等边三角形 B.钝角三角形
C .有一个角是 6 的直角三角形 D.等腰直角三角形
7.如图,在三棱锥 P ABC中, PA BC 3, PB AC 2,PC AB 5,
则三棱锥 P ABC外接球的体积为( )
A. 2 B. 3 C. 6 D.6
8.在正方体 ABCD A B C D 中, E为棱DC上的动点,F 为线段 B E的中点.给出下列四个
① B E AD ;②直线D F 与平面 ABB A 所成角不变;
试卷第 1页,共 4页
③点 F 到直线 AB的距离不变;④点 F 到 A,D,D ,A 四点的距离相等.其中,所有正确结论的序号为( )
A.②③ B.③④ C.①③④ D.①②④
二、多项选择题:本题共 4小题,每小题 5分,共 20分.在每小题给出的四个选项中,有多项符合题目要求,
全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
1 i
9.已知复数 z ,以下结论正确的是( )
1 i
A. z 2021是纯虚数 B. z i 2
C. z z 1 D.在复平面内,复数 z z i对应的点位于第三象限
10.某学校为了了解学生一周内在生活方面的支出情况,从全校学生中随机抽取 n名学生进行调查,得到
频率分布直方图如图所示,其中支出在[50,60]内的学
生有 60人,则下列说法正确的是( )
A.样本中数据的中位数小于 41
B.样本中支出不少于 40元的人数为 132
C.全校学生支出的众数约为 45元
D.若该校有 2000名学生,则约有 600人的支出在[50,60]内
11.已知 f (x) sin( x ) 0,| |
7
的图象关于点 ,0 对称,相邻两条对称轴的距离为 ,则下
2 12 2
列说法正确的是( )
π
A. 2,
6
B .将函数 f (x)的图象向右平移 6 个单位长度后,得到的图象关于 y轴对称
C
.函数 f (x)在 0, 上的单调递减区间为 2
,
3 2
D.为了得到 f (x)的图象,可以将函数 y sin 2x 的图象向右平移 6 个单位
12.已知正四面体的外接球、内切球的球面上各有一动点M 、 N,若线段MN的最小值为 6,则( )
A.正四面体的棱长为 6 B.正四面体的内切球的表面积为 6
C.正四面体的外接球的体积为8 6 D.线段MN的最大值为2 6
三、填空题:本大题共 4小题,每小题 5分,共 20分请将答案填在答题卡对应题号的位置上,填错位置,
书写不清,模棱两可均不得分.
13.某同学5次上学途中所花的时间(单位:分钟)分别为 x,y,8,10,12 .已知这组数据的平均数为10,
标准差为 2,则 x y的值为____________.
试卷第 2页,共 4页
14 .已知向量 a,b 满足 a 1, 3 ,b 1,0 ,则向量 a在b 上的投影向量为________.
15.如图,四边形 ABCD为正方形, AG 平面 ABCD, AG / /DF / /CE,若
AG AB 3,DF 2,CE 1,则VB EGD :VG BEF ______.
16.已知 ABC的内角 A,B,C所对的边分别为 a,b,c,且
sin B π cos
π 3
B
,若 ABC为钝角三角形, a c 3,则 外接圆
3 6 4
ABC
的半径 R的取值范围是__________.
四、解答题:本大题共 6小题,共 70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分 10分)平面内给定三个向量 a (2,5), b ( 1,2), c (4,1) .
(1) 求满足 a mb n c 的实数m, n;
(2)若 (a k c)//(3b a) ,求实数 k的值.
18.(本小题满分 12分)
已知 a,b,c分别为 ABC的内角 A,B,C所对的边,且满足 a c b sinA sinC sinB csinB
(1)求角A的大小;
(2)若 a 2 3,求 ABC面积的最大值.
19.(本小题满分 12分)如图,直三棱柱 ABC A1B1C1中, AC BC 1, ACB 120 , AA1 3 .
(1)证明: A1B1∥平面 ABC1;
(2)求点C到平面 ABC1的距离.
试卷第 3页,共 4页
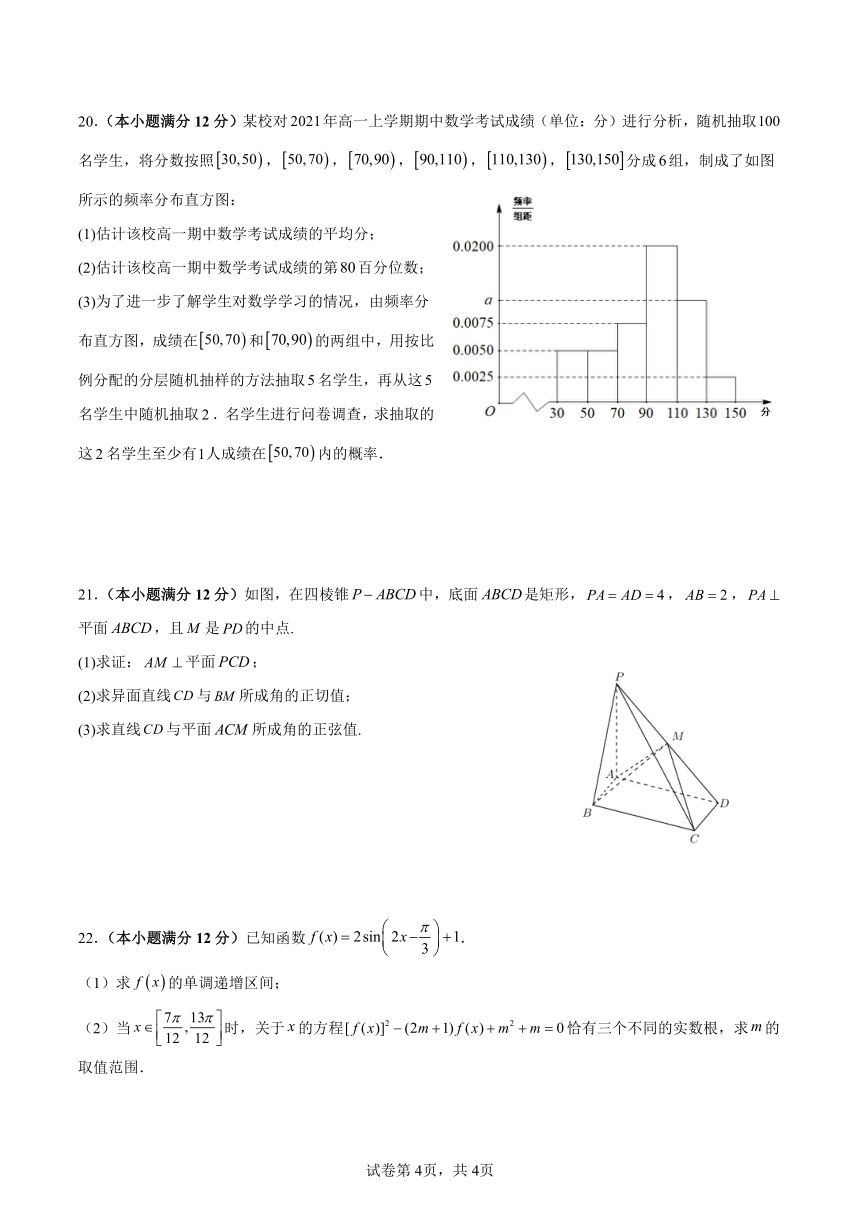
20.(本小题满分 12分)某校对 2021年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取100
名学生,将分数按照 30,50 , 50,70 , 70,90 , 90,110 , 110,130 , 130,150 分成 6组,制成了如图
所示的频率分布直方图:
(1)估计该校高一期中数学考试成绩的平均分;
(2)估计该校高一期中数学考试成绩的第80百分位数;
(3)为了进一步了解学生对数学学习的情况,由频率分
布直方图,成绩在 50,70 和 70,90 的两组中,用按比
例分配的分层随机抽样的方法抽取5名学生,再从这5
名学生中随机抽取 2.名学生进行问卷调查,求抽取的
这 2名学生至少有1人成绩在 50,70 内的概率.
21.(本小题满分 12分)如图,在四棱锥 P ABCD中,底面 ABCD是矩形,PA AD 4, AB 2,PA
平面 ABCD,且M 是 PD的中点.
(1)求证: AM 平面 PCD;
(2)求异面直线CD与 BM 所成角的正切值;
(3)求直线CD与平面 ACM 所成角的正弦值.
22.(本小题满分 12分)已知函数 f (x) 2sin 2x 1.
3
(1)求 f x 的单调递增区间;
7 13 2 ( )当 x , 时,关于 x的方程[ f (x)]2 (2m 1) f (x) m
2 m 0恰有三个不同的实数根,求m的
12 12
取值范围.
试卷第 4页,共 4页
参考答案
1 2 3 4 5 6 7 8
D B A A B A C C
9 10 11 12
ABD BCD BC ABD
13 14 15 16
2 1,0 2 :1 (1, 3)
1.D
2 i
【详解】解:因为 z i i 2 i,所以 z i 1 3i,所以 z的虚部为 3 .故选:D
i
2.B
【详解】因为感染人群中 O型血、A型血、B型血、AB型血的人数比为 4:3:3:2,
4 2
所以,抽取样本量为 n的样本中,O型血的人数为 n, AB型血的人数为 n,所以,
4 3 3 2 4 3 3 2
4 n 2 n 20,解得n 120 故选:B
4 3 3 2 4 3 3 2
3.A
【详解】由 cos sin 0可得1 sin2 0,则 sin 2 1,
2 cos2 sin2
3 sin 2 2 cos sin 因为 2 , cos sin
2
3sin2等式两边平方可得 2 4 1 sin 2 ,即3sin2 2 4sin2 4 0,
1 sin 2 2 1,解得 sin 2 .故选:A.
3
4.A
【详解】由题意向量 a x,1 ,b (1, y),c 1, 2 ,且 a c,b / /c ,
x 1 1 2 0 x 2
故得: ,解得 ,故 x y 0
1 2 y 1 0
,故选:A
y 2
5.B
【详解】对于 A,m , n ,m//n,则 , 可能相交,也可能平行,故 A错误‘
对于 B, 若 , =l,m l,m ,根据面面垂直的性质定理m ,故 B正确;
对于 C, 若 // ,m ,n ,则 m,n可能平行也可能异面,故 C错误;
对于 D,若m l,n l,m ,n ,由于不能确定 m,n是否相交,故不能确定 l ,故 D错误,故
选:B
答案第 1页,共 8页
6.A
A
【详解】 向量m (a, cos ), n (b, cos
B ) B A共线, a cos b cos ,
2 2 2 2
由正弦定理: sin Acos
B sin B cos A A A B B , 2sin cos cos 2sin cos
B cos A,
2 2 2 2 2 2 2 2
则 sin
A
sin B,
2 2
0 A 0 B A B , , ,即 A B.同理可得 B C. ABC形状为等边三角形.故选:A.
2 2 2 2 2 2
7.C
【详解】解:由题意, PA BC 3, PB AC 2, PC AB 5,
将三棱锥 P ABC放到长方体中,可得长方体的三条对角线分别为 3,2, 5,
设长方体的长、宽、高分别为 a,b,c,
则 a2 b2 3, a2 c2 2, c2 b2 5,解得a 1,b 2, c 3.
所以三棱锥 P ABC R 1 a2 b2 c2 6外接球的半径 .
2 2
4三棱锥 P ABC 3外接球的体积V R 6 .故选:C
3
8.C
【详解】如下图,当 E在棱DC上运动时,B E始终在平面 A B CD中,由 AD A D, AD CD,A D CD D
可得 AD 平面A B CD,所以B E AD ,故①正确,
此时点 F的轨迹为线段 F1F2 ,如下图可知, F1F2 //AB, F1F2 过正方形 ADD A 中心G且 F1F2 平面ADD A ,
故③④正确,
如下图,延长D F 与 AB的延长线交于H,连接 A H,则 A HD 即为直线D F 与平面 ABB A 所成角,
A D
当点H在 BM 上运动时, A D 不变而HD 在变,所以 sin A HD 不是定值,
HD
故②错误.
故选:C.
答案第 2页,共 8页
9.ABD
1 i 1 iz 1 i 2i【详解】 i1 i 1 i 1 i 2
对于 A, z2021 i2021 i4 505 1 i, z2021为纯虚数,A正确;
对于 B, z i 2i 2,B正确;
对于 C, z z i i i2 1,C错误;
对于 D, z z i i i2 1 i, z z i对应的点为 1, 1 ,位于第三象限,D正确.故选:ABD.
10.BCD
【详解】在 A中,设样本数据的中位数为 x,则 0.01 0.024 10 x 40 0.036 0.5,解得 x≈44.44>41,
故 A错误;
在 B中,样本中支出在 50,60 内的频率为1 0.01 0.024 0.036 10 0.3,样本中支出不少于 40元的人
0.36 60
数为 60 132,故 B正确;
0
40 50
在 C中,由频率分布直方图得样本中学生支出的众数约为 45(元),所以全校学生支出的众数约
2
为 45元,故 C正确;
在 D中,若该校有 2000名学生,则约有 2000×0.3=600人的支出在 50,60 内,故 D正确.
故选:BCD.
11.BC
【详解】解:因为相邻两条对称轴的距离为 ,故周期为 ,则 2,
2
7
图象关于点 ,0
对称,则 2
7
k ,因为 | |
,所以 ,A错;
12 12 2 6
f (x) sin(2x 6 )
f (x) ,将函数 的图象向右平移 6 个单位长度后得
y sin 2x cos2x,该函数是偶函数,
2
图象关于 y轴对称,B正确;
令 2k
3
2x 2k k x 5 ,得 k ,k Z,
2 6 2 3 6
所以函数 f (x)
0, 在 上的单调递减区间为 , 2 3 2
,C正确;
为了得到 f (x)
的图象,应该将函数 y sin 2x的图象向右平移 12 个单位,D错.故选:BC.
答案第 3页,共 8页
12.ABD
2
【详解】设这个四面体的棱长为 a,则此四面体可看作棱长为 a的正方体截得的,所以四面体的外接球
2
即为正方体的外接球,外接球直径为正方体的对角线长,
2
2 6 6
设外接球的半径为 R,内切球的半径为 r,则 2R 3 a a,所以R a,
2 2 4
2
3 6 1 1
四面体的高为 h a2 a a,则等体积法可得 Sh 4 Sr r
1 h 6,所以 a,
3 3 3 3 4 12
R r 6 6由题意得 ,所以 a 6 a 6,解得 a 6所以 A正确,
4 12
3
6 4 4 3 6
所以 R 6 3 6 ,所以外接球的体积为 R3 27 6 ,所以 C错误,
4 2 3 3
2
2
6 6 6
因为内切球半径为 r 6 ,所以内切球的表面积为 4 r 2 4 6 ,所以 B正确,12 2 2
线段MN 3 6 6的最大值为R r 2 6 ,所以 D正确,故选:ABD
2 2
13. 2
1
【详解】平均数为 (x y 10 12 8) 10 x y 205 ,即 ①,
1
方差为 [(x 10)2 (y 10)2 (10 10)2 (12 10)2 (8 10)2 ] 2,即 (x 10)2 (y 10)2 25 ②,
由①②解得 x 9, y 11或 x 11, y 9,
所以当 x 9, y 11时, x y 2;当 x 11, y 9, x y 2 故答案为: 2.
14. 1,0
a
b
【详解】由题知, a在b 上的投影为 a cos a,b ,又 a 1, 3 ,b 1,0b ,
所以 a b 1 1 3 0 1 , b 12 02 1 ;
所以 a cos a,b 1 ,即 a在b 上的投影为 1 ;
b
又b 的单位向量为 1,0 b ,所以 a在b 上的投影向量为 1,0 故答案为: 1,0 .
答案第 4页,共 8页
15. 2 :1
【详解】将几何体补全为正方体,如下图示,
VG BEF VABCD GIHJ VG HEBJ VG HIFE VB CDFE VB DFGA
27 1 3 1 5 3 1 3 1 3 3 1 3 1 3 3 1 3 1 5 3 3
3 2 3 2 3 2 3 2 .
VB EGD VABCD GIHJ VG HEBJ VG HIDE VE BCD VG ABD
27 1 3 1 5 3 1 3 1 5 3 1 1 1 1 3 3 3 1 3 3 6 .
3 2 3 2 3 2 3 2
所以VB EGD :VG BEF 2 :1 .故答案为: 2 :1
16. (1, 3)
π π 3 π 3 π 3
【详解】因为 sin B cos B ,所以 sin2 B sin B ,
3 6 4 3 4 3 2
0 B π π B π 4π B π 2π B π又因为: ,所以 ,
3 3 3 3 3 3
a c a c 3
由正弦定理有: 2R ,
sin A sinC sin A sinC sin A sinC
sin A sinC sin A 2π sin A 3而 sin A
3
cos A 3 sin A
π
,
3 2 2 6
π 2π 2π π 5π
又因为 ABC为钝角三角形,不妨设 A 1 π, A sin A 3则 ,则 ,
2 3 3 6 6 2 6 2
3 3 3
所以 sin A+sinC ,所以 ABC外接圆的半径 R (1, 3) .故答案为: (1, 3) .
2 2 2 sin A sinC
17 (1) . 解:因为 a (2,5), b ( 1,2), c (4,1),且 a mb n c ,
m 4n 2
2,5 m 1,2 n 4,1 m 4n, 2m n , ,解得m 2, n 1
2m n 5
(2) 解: a k c 2,5 k 4,1 4k 2,k 5 ,3b a 3 1,2 2,5 5,1 .
因为 (a k c)//(3b a) , 4k 2 5 k 5 9k 27 0,解得 k 3 .
答案第 5页,共 8页
18.(1)在 ABC中,由题意及正弦定理得 a c b a c b bc,整理得b2 c2 a 2 bc,由余弦定理
b2 c2 2
得 cosA a bc 1 ,因为0 A ,所以 A ;
2bc 2bc 2 3
(2)方法一:由(1)知,A ,又 a 2 3,所以12 b2 c2 bc 2bc bc bc ,所以 bc 12,当且仅当
3
1 1 3
b c 2 3时,等号成立,所以 S ABC bcsinA 12 3 3 ;方法二:由(1)知,A ,又 a 2 3,max 2 2 2 3
a b c 2 3
4
所以由正弦定理,知 sinA sinB sinC ,所以b 4sinB,c 4sinC,所以sin
3
2
S 1 ABC bcsinA 8sinBsinC
3
4 3sinBsinC,又因为 B C ,所以
2 2 3
4 3sinBsinC 4 3sinBsin 2 B
4 3sinB
3
cosB
1
sinB 3 2 3 sin2B
1 cos2B
3
2 2 2 2
2 3sin 2B
3 B C 2 2 7 ,因为 ,所以0 B , 2B ,所以当 2B ,即 B
6 3 3 6 6 6 6 2 3
时, ABC的面积取得最大值,最大值为3 3 .
19.(1)证明:∵ ABC A1B1C1为直三棱柱,∴ A1B1∥ AB
又 A1B1 平面 ABC1, AB 平面 ABC1,∴ A1B1∥平面 ABC1
(2)解:在 ABC中, AC BC 1, ACB 120 ,
则 AB 3, ABC 1 3的面积为 1 1 sin120
2 4
∵ ABC A1B1C1为直三棱柱,∴CC1⊥平面 ABC,
∴CC1⊥AC,从而 AC1 BC1 2
取 AB的中点D,连接C1D,则C1D AB,C1D
13
2
ABC 1 3 13 39∴ 1的面积为 ,
2 2 4
设点C到平面 ABC1的距离为 h,
V =V 1 3 1 39 39由于 C1 ABC C ABC1 ∴ 3 h,解得 h 3 4 3 4 13
故点C到平面 ABC 391的距离为 .
13
答案第 6页,共 8页
20. (1)解:由0.005 20 0.005 20 0.0075 20 0.02 20 a 20 0.0025 20 1,得 a 0.01.
数学成绩在: 30,50 频率0.0050 20 0.1, 50,70 频率 0.0050 20 0.1,
70,90 频率0.0075 20 0.15, 90,110 频率0.0200 20 0.4,
110,130 频率0.0100 20 0.2, 130,150 频率 0.0025 20 0.05,
样本平均值为: 40 0.1 60 0.1 80 0.15 100 0.4 120 0.2 140 0.05 93,
可以估计样本数据中数学成绩均值为93分,据此可以估计该校高一下学期期中数学考试成绩估计93分.
(2)解:由 1 知样本数据中数学考试成绩在110分以下所占比例为0.1 0.1 0.15 0.4 0.75,
在130分以下所占比例为0.75 0.2 0.95
因此,第80百分位数一定位于 110,130 110 20 0.8 0.75内,由 115,
0.95 0.75
可以估计样本数据的第80百分位数约为115分,
据此可以估计该校高一下学期期中数学考试成绩第80百分位数约为115分.
(3)解:由题意可知, 50,70 分数段的人数为100 0.1 10 (人),
70,90 分数段的人数为100 0.15 15 (人).
用按比例分配的分层随机抽样的方法抽取5名学生,则需在 50,70 分数段内抽 2人,分别记为 A1, A2,需
在 70,90 分数段内抽3人,分别记为 B1, B2, B3,
设“从样本中任取 2人,至少有1人在分数段 50,70 内”为事件A,
则样本空间 A1A2 , A1B1, A1B2 , A1B3, A2B1, A2B2 , A2B3,B1B2 ,B1B3,B2B3 共包含10个样本点
而A的对立事件 A B1B2 ,B1B3,B2B3 包含3个样本点
所以 P A 3 ,所以 P A 1 P A 7 7 ,即抽取的这 2名学生至少有1人在 50,70 内的概率为 .10 10 10
21.(1)解:∵ PA 平面 ABCD,CD 平面 ABCD,∴ PA CD,又四边形 ABCD是矩形,
∴CD DA,∵DA PA A,∴CD 平面 PAD,∵ AM 平面 PAD,∴CD AM ,
又M 是 PD的中点, PA AD 4,∴ AM PD,∵CD PD D,所以 AM 平面 PCD .
(2)解:∵底面 ABCD是矩形,∴CD / /BA,∴异面直线CD与 BM所成角为直线 BA与直线 BM 所成的角,
由(1)得CD 平面 PAD,∴ BA⊥平面 PAD,
∵ AM 平面 PAD,∴ BA AM ,∴ BAM 为直角三角形,
答案第 7页,共 8页
又M 是 PD的中点,PA AD 4,∴ AM 2 2,∴在Rt BAM中, ABM 为异面直线CD与 BM 所成角,
故 tan ABM
AM
2,∴异面直线CD与 BM 所成角的正切值为 .
AB 2
(3)解:取 AD中点为 N ,连接MN, AC,在△PAD中,M ,N分别为线段 PD, AD的中点,
故MN / /PA,MN
1
PA 2,∵ PA 平面 ABCD,∴MN 平面 ABCD,
2
V 1 MN 1∴ M ACD AD CD
8
,由(1)得 AM 平面 PCD,∵MC 平面 PCD,∴ AM MC,
3 2 3
∵ PA AD 4,∴ PD 4 2,MD 2 2
1
又 AB CD 2,∴MC 2 3 ,∴ S AMC AM MC 2 6,2
设点D到平面 AMC的距离为 h,直线CD与平面 ACM所成角为 ,
1 8 4 h 6
则VD AMC h S V3 AMC M ACD
,解得: h ,故
3 6 sin
,
CD 3
所以直线CD与平面 ACM 6所成角的正弦值为 .
3
5
22.【详解】(1)令 2k 2x 2k (k Z)2 3 2 ,解得 k x k (k Z)12 12 ,
f x k ,k 5 故 的单调递增区间为 (k Z) 12 12
(2) [ f (x)]2 (2m 1) f (x) m2 m 0等价于 [ f (x) (m 1)][ f (x) m] 0,
解得 f x m 1或 f x m,
x 7 因为 ,
13 5 11
,所以 2x , , f (x) [ 1,2],如图,绘出函数
12 12 3 6 6
f x 的图像,方程 [ f (x)]2 (2m 1) f (x) m2 m 0有三个不同的实数根
等价于 f (x) m 1有一个实数解且 f x m有两个不同的实数解
或 f x m 1有两个不同的实数解且 f x m有一个实数解,
①当m 1或m 2时, f x m无解,不符合题意;
②当m 1时,则m 1 0, f x m有一个实数解, f x m 1有两个不同的实数解,符合题意;
③当 1 m 0时,则0 m 1 2, f x m有两个不同的实数解, f x m 1有一个实数解,符合题意;
④当0 m 2时,则1 m 1 3, f x m有一个实数解, f x m 1至多有一个实数解,不符合题意.
综上,m的取值范围为[ 1,0].
答案第 8页,共 8页
数学
一、单项选择题:本大题共 8小题,每小题 5分,共 40分,在每小题给出的四个选项中,只有一项是符合
题目要求的.
1.已知复数 z满足 z i i 2 i,则 z的虚部为( )
A. i B. 3i C. 1 D. 3
2.为了研究某种病毒与血型之间的关系,决定从被感染的人群中抽取样本进行调查,这些感染人群中 O型
血、A型血、B型血、AB型血的人数比为 4:3:3:2,现用比例分配的分层随机抽样方法抽取一个样本量为 n的
样本,已知样本中 O型血的人数比 AB型血的人数多 20,则 n ( )
A.100 B.120 C.200 D.240
2 cos2 sin2
3 3 sin 2 .若
cos
,则 sin 2 ( )
4
2 2 1 1A. B. C. D.
3 3 3 3
4.设 x, y R
,向量a x,1 ,b (1, y),c 1, 2 , a c 且 ,b / /c ,则 x y ( )
A.0 B.1 C.2 D.3
5.设 , 是互不重合的平面, l,m, n是互不重合的直线,下列命题中正确的是( )
A.若m , n ,m//n,则 // B.若 , =l,m l,m ,则m
C.若 // ,m ,n ,则m//n D.若m l,n l,m ,n ,则 l
6.在 ABC中,角 A,B,C的对边分别为 a,b,c ,已知三个向量m a, cos
A
,n b, cos
B
, p c, cos
C
共
2 2 2
线,则 ABC的形状为( )
A.等边三角形 B.钝角三角形
C .有一个角是 6 的直角三角形 D.等腰直角三角形
7.如图,在三棱锥 P ABC中, PA BC 3, PB AC 2,PC AB 5,
则三棱锥 P ABC外接球的体积为( )
A. 2 B. 3 C. 6 D.6
8.在正方体 ABCD A B C D 中, E为棱DC上的动点,F 为线段 B E的中点.给出下列四个
① B E AD ;②直线D F 与平面 ABB A 所成角不变;
试卷第 1页,共 4页
③点 F 到直线 AB的距离不变;④点 F 到 A,D,D ,A 四点的距离相等.其中,所有正确结论的序号为( )
A.②③ B.③④ C.①③④ D.①②④
二、多项选择题:本题共 4小题,每小题 5分,共 20分.在每小题给出的四个选项中,有多项符合题目要求,
全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
1 i
9.已知复数 z ,以下结论正确的是( )
1 i
A. z 2021是纯虚数 B. z i 2
C. z z 1 D.在复平面内,复数 z z i对应的点位于第三象限
10.某学校为了了解学生一周内在生活方面的支出情况,从全校学生中随机抽取 n名学生进行调查,得到
频率分布直方图如图所示,其中支出在[50,60]内的学
生有 60人,则下列说法正确的是( )
A.样本中数据的中位数小于 41
B.样本中支出不少于 40元的人数为 132
C.全校学生支出的众数约为 45元
D.若该校有 2000名学生,则约有 600人的支出在[50,60]内
11.已知 f (x) sin( x ) 0,| |
7
的图象关于点 ,0 对称,相邻两条对称轴的距离为 ,则下
2 12 2
列说法正确的是( )
π
A. 2,
6
B .将函数 f (x)的图象向右平移 6 个单位长度后,得到的图象关于 y轴对称
C
.函数 f (x)在 0, 上的单调递减区间为 2
,
3 2
D.为了得到 f (x)的图象,可以将函数 y sin 2x 的图象向右平移 6 个单位
12.已知正四面体的外接球、内切球的球面上各有一动点M 、 N,若线段MN的最小值为 6,则( )
A.正四面体的棱长为 6 B.正四面体的内切球的表面积为 6
C.正四面体的外接球的体积为8 6 D.线段MN的最大值为2 6
三、填空题:本大题共 4小题,每小题 5分,共 20分请将答案填在答题卡对应题号的位置上,填错位置,
书写不清,模棱两可均不得分.
13.某同学5次上学途中所花的时间(单位:分钟)分别为 x,y,8,10,12 .已知这组数据的平均数为10,
标准差为 2,则 x y的值为____________.
试卷第 2页,共 4页
14 .已知向量 a,b 满足 a 1, 3 ,b 1,0 ,则向量 a在b 上的投影向量为________.
15.如图,四边形 ABCD为正方形, AG 平面 ABCD, AG / /DF / /CE,若
AG AB 3,DF 2,CE 1,则VB EGD :VG BEF ______.
16.已知 ABC的内角 A,B,C所对的边分别为 a,b,c,且
sin B π cos
π 3
B
,若 ABC为钝角三角形, a c 3,则 外接圆
3 6 4
ABC
的半径 R的取值范围是__________.
四、解答题:本大题共 6小题,共 70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分 10分)平面内给定三个向量 a (2,5), b ( 1,2), c (4,1) .
(1) 求满足 a mb n c 的实数m, n;
(2)若 (a k c)//(3b a) ,求实数 k的值.
18.(本小题满分 12分)
已知 a,b,c分别为 ABC的内角 A,B,C所对的边,且满足 a c b sinA sinC sinB csinB
(1)求角A的大小;
(2)若 a 2 3,求 ABC面积的最大值.
19.(本小题满分 12分)如图,直三棱柱 ABC A1B1C1中, AC BC 1, ACB 120 , AA1 3 .
(1)证明: A1B1∥平面 ABC1;
(2)求点C到平面 ABC1的距离.
试卷第 3页,共 4页
20.(本小题满分 12分)某校对 2021年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取100
名学生,将分数按照 30,50 , 50,70 , 70,90 , 90,110 , 110,130 , 130,150 分成 6组,制成了如图
所示的频率分布直方图:
(1)估计该校高一期中数学考试成绩的平均分;
(2)估计该校高一期中数学考试成绩的第80百分位数;
(3)为了进一步了解学生对数学学习的情况,由频率分
布直方图,成绩在 50,70 和 70,90 的两组中,用按比
例分配的分层随机抽样的方法抽取5名学生,再从这5
名学生中随机抽取 2.名学生进行问卷调查,求抽取的
这 2名学生至少有1人成绩在 50,70 内的概率.
21.(本小题满分 12分)如图,在四棱锥 P ABCD中,底面 ABCD是矩形,PA AD 4, AB 2,PA
平面 ABCD,且M 是 PD的中点.
(1)求证: AM 平面 PCD;
(2)求异面直线CD与 BM 所成角的正切值;
(3)求直线CD与平面 ACM 所成角的正弦值.
22.(本小题满分 12分)已知函数 f (x) 2sin 2x 1.
3
(1)求 f x 的单调递增区间;
7 13 2 ( )当 x , 时,关于 x的方程[ f (x)]2 (2m 1) f (x) m
2 m 0恰有三个不同的实数根,求m的
12 12
取值范围.
试卷第 4页,共 4页
参考答案
1 2 3 4 5 6 7 8
D B A A B A C C
9 10 11 12
ABD BCD BC ABD
13 14 15 16
2 1,0 2 :1 (1, 3)
1.D
2 i
【详解】解:因为 z i i 2 i,所以 z i 1 3i,所以 z的虚部为 3 .故选:D
i
2.B
【详解】因为感染人群中 O型血、A型血、B型血、AB型血的人数比为 4:3:3:2,
4 2
所以,抽取样本量为 n的样本中,O型血的人数为 n, AB型血的人数为 n,所以,
4 3 3 2 4 3 3 2
4 n 2 n 20,解得n 120 故选:B
4 3 3 2 4 3 3 2
3.A
【详解】由 cos sin 0可得1 sin2 0,则 sin 2 1,
2 cos2 sin2
3 sin 2 2 cos sin 因为 2 , cos sin
2
3sin2等式两边平方可得 2 4 1 sin 2 ,即3sin2 2 4sin2 4 0,
1 sin 2 2 1,解得 sin 2 .故选:A.
3
4.A
【详解】由题意向量 a x,1 ,b (1, y),c 1, 2 ,且 a c,b / /c ,
x 1 1 2 0 x 2
故得: ,解得 ,故 x y 0
1 2 y 1 0
,故选:A
y 2
5.B
【详解】对于 A,m , n ,m//n,则 , 可能相交,也可能平行,故 A错误‘
对于 B, 若 , =l,m l,m ,根据面面垂直的性质定理m ,故 B正确;
对于 C, 若 // ,m ,n ,则 m,n可能平行也可能异面,故 C错误;
对于 D,若m l,n l,m ,n ,由于不能确定 m,n是否相交,故不能确定 l ,故 D错误,故
选:B
答案第 1页,共 8页
6.A
A
【详解】 向量m (a, cos ), n (b, cos
B ) B A共线, a cos b cos ,
2 2 2 2
由正弦定理: sin Acos
B sin B cos A A A B B , 2sin cos cos 2sin cos
B cos A,
2 2 2 2 2 2 2 2
则 sin
A
sin B,
2 2
0 A 0 B A B , , ,即 A B.同理可得 B C. ABC形状为等边三角形.故选:A.
2 2 2 2 2 2
7.C
【详解】解:由题意, PA BC 3, PB AC 2, PC AB 5,
将三棱锥 P ABC放到长方体中,可得长方体的三条对角线分别为 3,2, 5,
设长方体的长、宽、高分别为 a,b,c,
则 a2 b2 3, a2 c2 2, c2 b2 5,解得a 1,b 2, c 3.
所以三棱锥 P ABC R 1 a2 b2 c2 6外接球的半径 .
2 2
4三棱锥 P ABC 3外接球的体积V R 6 .故选:C
3
8.C
【详解】如下图,当 E在棱DC上运动时,B E始终在平面 A B CD中,由 AD A D, AD CD,A D CD D
可得 AD 平面A B CD,所以B E AD ,故①正确,
此时点 F的轨迹为线段 F1F2 ,如下图可知, F1F2 //AB, F1F2 过正方形 ADD A 中心G且 F1F2 平面ADD A ,
故③④正确,
如下图,延长D F 与 AB的延长线交于H,连接 A H,则 A HD 即为直线D F 与平面 ABB A 所成角,
A D
当点H在 BM 上运动时, A D 不变而HD 在变,所以 sin A HD 不是定值,
HD
故②错误.
故选:C.
答案第 2页,共 8页
9.ABD
1 i 1 iz 1 i 2i【详解】 i1 i 1 i 1 i 2
对于 A, z2021 i2021 i4 505 1 i, z2021为纯虚数,A正确;
对于 B, z i 2i 2,B正确;
对于 C, z z i i i2 1,C错误;
对于 D, z z i i i2 1 i, z z i对应的点为 1, 1 ,位于第三象限,D正确.故选:ABD.
10.BCD
【详解】在 A中,设样本数据的中位数为 x,则 0.01 0.024 10 x 40 0.036 0.5,解得 x≈44.44>41,
故 A错误;
在 B中,样本中支出在 50,60 内的频率为1 0.01 0.024 0.036 10 0.3,样本中支出不少于 40元的人
0.36 60
数为 60 132,故 B正确;
0
40 50
在 C中,由频率分布直方图得样本中学生支出的众数约为 45(元),所以全校学生支出的众数约
2
为 45元,故 C正确;
在 D中,若该校有 2000名学生,则约有 2000×0.3=600人的支出在 50,60 内,故 D正确.
故选:BCD.
11.BC
【详解】解:因为相邻两条对称轴的距离为 ,故周期为 ,则 2,
2
7
图象关于点 ,0
对称,则 2
7
k ,因为 | |
,所以 ,A错;
12 12 2 6
f (x) sin(2x 6 )
f (x) ,将函数 的图象向右平移 6 个单位长度后得
y sin 2x cos2x,该函数是偶函数,
2
图象关于 y轴对称,B正确;
令 2k
3
2x 2k k x 5 ,得 k ,k Z,
2 6 2 3 6
所以函数 f (x)
0, 在 上的单调递减区间为 , 2 3 2
,C正确;
为了得到 f (x)
的图象,应该将函数 y sin 2x的图象向右平移 12 个单位,D错.故选:BC.
答案第 3页,共 8页
12.ABD
2
【详解】设这个四面体的棱长为 a,则此四面体可看作棱长为 a的正方体截得的,所以四面体的外接球
2
即为正方体的外接球,外接球直径为正方体的对角线长,
2
2 6 6
设外接球的半径为 R,内切球的半径为 r,则 2R 3 a a,所以R a,
2 2 4
2
3 6 1 1
四面体的高为 h a2 a a,则等体积法可得 Sh 4 Sr r
1 h 6,所以 a,
3 3 3 3 4 12
R r 6 6由题意得 ,所以 a 6 a 6,解得 a 6所以 A正确,
4 12
3
6 4 4 3 6
所以 R 6 3 6 ,所以外接球的体积为 R3 27 6 ,所以 C错误,
4 2 3 3
2
2
6 6 6
因为内切球半径为 r 6 ,所以内切球的表面积为 4 r 2 4 6 ,所以 B正确,12 2 2
线段MN 3 6 6的最大值为R r 2 6 ,所以 D正确,故选:ABD
2 2
13. 2
1
【详解】平均数为 (x y 10 12 8) 10 x y 205 ,即 ①,
1
方差为 [(x 10)2 (y 10)2 (10 10)2 (12 10)2 (8 10)2 ] 2,即 (x 10)2 (y 10)2 25 ②,
由①②解得 x 9, y 11或 x 11, y 9,
所以当 x 9, y 11时, x y 2;当 x 11, y 9, x y 2 故答案为: 2.
14. 1,0
a
b
【详解】由题知, a在b 上的投影为 a cos a,b ,又 a 1, 3 ,b 1,0b ,
所以 a b 1 1 3 0 1 , b 12 02 1 ;
所以 a cos a,b 1 ,即 a在b 上的投影为 1 ;
b
又b 的单位向量为 1,0 b ,所以 a在b 上的投影向量为 1,0 故答案为: 1,0 .
答案第 4页,共 8页
15. 2 :1
【详解】将几何体补全为正方体,如下图示,
VG BEF VABCD GIHJ VG HEBJ VG HIFE VB CDFE VB DFGA
27 1 3 1 5 3 1 3 1 3 3 1 3 1 3 3 1 3 1 5 3 3
3 2 3 2 3 2 3 2 .
VB EGD VABCD GIHJ VG HEBJ VG HIDE VE BCD VG ABD
27 1 3 1 5 3 1 3 1 5 3 1 1 1 1 3 3 3 1 3 3 6 .
3 2 3 2 3 2 3 2
所以VB EGD :VG BEF 2 :1 .故答案为: 2 :1
16. (1, 3)
π π 3 π 3 π 3
【详解】因为 sin B cos B ,所以 sin2 B sin B ,
3 6 4 3 4 3 2
0 B π π B π 4π B π 2π B π又因为: ,所以 ,
3 3 3 3 3 3
a c a c 3
由正弦定理有: 2R ,
sin A sinC sin A sinC sin A sinC
sin A sinC sin A 2π sin A 3而 sin A
3
cos A 3 sin A
π
,
3 2 2 6
π 2π 2π π 5π
又因为 ABC为钝角三角形,不妨设 A 1 π, A sin A 3则 ,则 ,
2 3 3 6 6 2 6 2
3 3 3
所以 sin A+sinC ,所以 ABC外接圆的半径 R (1, 3) .故答案为: (1, 3) .
2 2 2 sin A sinC
17 (1) . 解:因为 a (2,5), b ( 1,2), c (4,1),且 a mb n c ,
m 4n 2
2,5 m 1,2 n 4,1 m 4n, 2m n , ,解得m 2, n 1
2m n 5
(2) 解: a k c 2,5 k 4,1 4k 2,k 5 ,3b a 3 1,2 2,5 5,1 .
因为 (a k c)//(3b a) , 4k 2 5 k 5 9k 27 0,解得 k 3 .
答案第 5页,共 8页
18.(1)在 ABC中,由题意及正弦定理得 a c b a c b bc,整理得b2 c2 a 2 bc,由余弦定理
b2 c2 2
得 cosA a bc 1 ,因为0 A ,所以 A ;
2bc 2bc 2 3
(2)方法一:由(1)知,A ,又 a 2 3,所以12 b2 c2 bc 2bc bc bc ,所以 bc 12,当且仅当
3
1 1 3
b c 2 3时,等号成立,所以 S ABC bcsinA 12 3 3 ;方法二:由(1)知,A ,又 a 2 3,max 2 2 2 3
a b c 2 3
4
所以由正弦定理,知 sinA sinB sinC ,所以b 4sinB,c 4sinC,所以sin
3
2
S 1 ABC bcsinA 8sinBsinC
3
4 3sinBsinC,又因为 B C ,所以
2 2 3
4 3sinBsinC 4 3sinBsin 2 B
4 3sinB
3
cosB
1
sinB 3 2 3 sin2B
1 cos2B
3
2 2 2 2
2 3sin 2B
3 B C 2 2 7 ,因为 ,所以0 B , 2B ,所以当 2B ,即 B
6 3 3 6 6 6 6 2 3
时, ABC的面积取得最大值,最大值为3 3 .
19.(1)证明:∵ ABC A1B1C1为直三棱柱,∴ A1B1∥ AB
又 A1B1 平面 ABC1, AB 平面 ABC1,∴ A1B1∥平面 ABC1
(2)解:在 ABC中, AC BC 1, ACB 120 ,
则 AB 3, ABC 1 3的面积为 1 1 sin120
2 4
∵ ABC A1B1C1为直三棱柱,∴CC1⊥平面 ABC,
∴CC1⊥AC,从而 AC1 BC1 2
取 AB的中点D,连接C1D,则C1D AB,C1D
13
2
ABC 1 3 13 39∴ 1的面积为 ,
2 2 4
设点C到平面 ABC1的距离为 h,
V =V 1 3 1 39 39由于 C1 ABC C ABC1 ∴ 3 h,解得 h 3 4 3 4 13
故点C到平面 ABC 391的距离为 .
13
答案第 6页,共 8页
20. (1)解:由0.005 20 0.005 20 0.0075 20 0.02 20 a 20 0.0025 20 1,得 a 0.01.
数学成绩在: 30,50 频率0.0050 20 0.1, 50,70 频率 0.0050 20 0.1,
70,90 频率0.0075 20 0.15, 90,110 频率0.0200 20 0.4,
110,130 频率0.0100 20 0.2, 130,150 频率 0.0025 20 0.05,
样本平均值为: 40 0.1 60 0.1 80 0.15 100 0.4 120 0.2 140 0.05 93,
可以估计样本数据中数学成绩均值为93分,据此可以估计该校高一下学期期中数学考试成绩估计93分.
(2)解:由 1 知样本数据中数学考试成绩在110分以下所占比例为0.1 0.1 0.15 0.4 0.75,
在130分以下所占比例为0.75 0.2 0.95
因此,第80百分位数一定位于 110,130 110 20 0.8 0.75内,由 115,
0.95 0.75
可以估计样本数据的第80百分位数约为115分,
据此可以估计该校高一下学期期中数学考试成绩第80百分位数约为115分.
(3)解:由题意可知, 50,70 分数段的人数为100 0.1 10 (人),
70,90 分数段的人数为100 0.15 15 (人).
用按比例分配的分层随机抽样的方法抽取5名学生,则需在 50,70 分数段内抽 2人,分别记为 A1, A2,需
在 70,90 分数段内抽3人,分别记为 B1, B2, B3,
设“从样本中任取 2人,至少有1人在分数段 50,70 内”为事件A,
则样本空间 A1A2 , A1B1, A1B2 , A1B3, A2B1, A2B2 , A2B3,B1B2 ,B1B3,B2B3 共包含10个样本点
而A的对立事件 A B1B2 ,B1B3,B2B3 包含3个样本点
所以 P A 3 ,所以 P A 1 P A 7 7 ,即抽取的这 2名学生至少有1人在 50,70 内的概率为 .10 10 10
21.(1)解:∵ PA 平面 ABCD,CD 平面 ABCD,∴ PA CD,又四边形 ABCD是矩形,
∴CD DA,∵DA PA A,∴CD 平面 PAD,∵ AM 平面 PAD,∴CD AM ,
又M 是 PD的中点, PA AD 4,∴ AM PD,∵CD PD D,所以 AM 平面 PCD .
(2)解:∵底面 ABCD是矩形,∴CD / /BA,∴异面直线CD与 BM所成角为直线 BA与直线 BM 所成的角,
由(1)得CD 平面 PAD,∴ BA⊥平面 PAD,
∵ AM 平面 PAD,∴ BA AM ,∴ BAM 为直角三角形,
答案第 7页,共 8页
又M 是 PD的中点,PA AD 4,∴ AM 2 2,∴在Rt BAM中, ABM 为异面直线CD与 BM 所成角,
故 tan ABM
AM
2,∴异面直线CD与 BM 所成角的正切值为 .
AB 2
(3)解:取 AD中点为 N ,连接MN, AC,在△PAD中,M ,N分别为线段 PD, AD的中点,
故MN / /PA,MN
1
PA 2,∵ PA 平面 ABCD,∴MN 平面 ABCD,
2
V 1 MN 1∴ M ACD AD CD
8
,由(1)得 AM 平面 PCD,∵MC 平面 PCD,∴ AM MC,
3 2 3
∵ PA AD 4,∴ PD 4 2,MD 2 2
1
又 AB CD 2,∴MC 2 3 ,∴ S AMC AM MC 2 6,2
设点D到平面 AMC的距离为 h,直线CD与平面 ACM所成角为 ,
1 8 4 h 6
则VD AMC h S V3 AMC M ACD
,解得: h ,故
3 6 sin
,
CD 3
所以直线CD与平面 ACM 6所成角的正弦值为 .
3
5
22.【详解】(1)令 2k 2x 2k (k Z)2 3 2 ,解得 k x k (k Z)12 12 ,
f x k ,k 5 故 的单调递增区间为 (k Z) 12 12
(2) [ f (x)]2 (2m 1) f (x) m2 m 0等价于 [ f (x) (m 1)][ f (x) m] 0,
解得 f x m 1或 f x m,
x 7 因为 ,
13 5 11
,所以 2x , , f (x) [ 1,2],如图,绘出函数
12 12 3 6 6
f x 的图像,方程 [ f (x)]2 (2m 1) f (x) m2 m 0有三个不同的实数根
等价于 f (x) m 1有一个实数解且 f x m有两个不同的实数解
或 f x m 1有两个不同的实数解且 f x m有一个实数解,
①当m 1或m 2时, f x m无解,不符合题意;
②当m 1时,则m 1 0, f x m有一个实数解, f x m 1有两个不同的实数解,符合题意;
③当 1 m 0时,则0 m 1 2, f x m有两个不同的实数解, f x m 1有一个实数解,符合题意;
④当0 m 2时,则1 m 1 3, f x m有一个实数解, f x m 1至多有一个实数解,不符合题意.
综上,m的取值范围为[ 1,0].
答案第 8页,共 8页
同课章节目录
