有理数乘法(1)[上学期]
文档属性
| 名称 | 有理数乘法(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 315.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-22 12:05:00 | ||
图片预览





文档简介
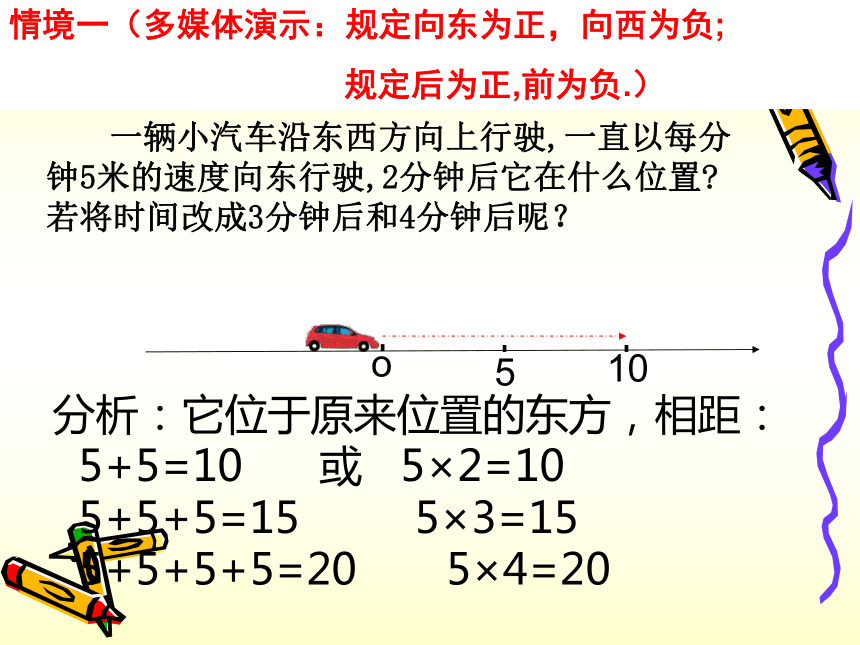
课件22张PPT。有理数乘法重庆涪陵第十五中学李小银(一)o510 一辆小汽车沿东西方向上行驶,一直以每分钟5米的速度向东行驶,2分钟后它在什么位置? 若将时间改成3分钟后和4分钟后呢? 分析:它位于原来位置的东方,相距:
5+5=10 或 5×2=10
5+5+5=15 5×3=15
5+5+5+5=20 5×4=20情境一(多媒体演示:规定向东为正,向西为负;
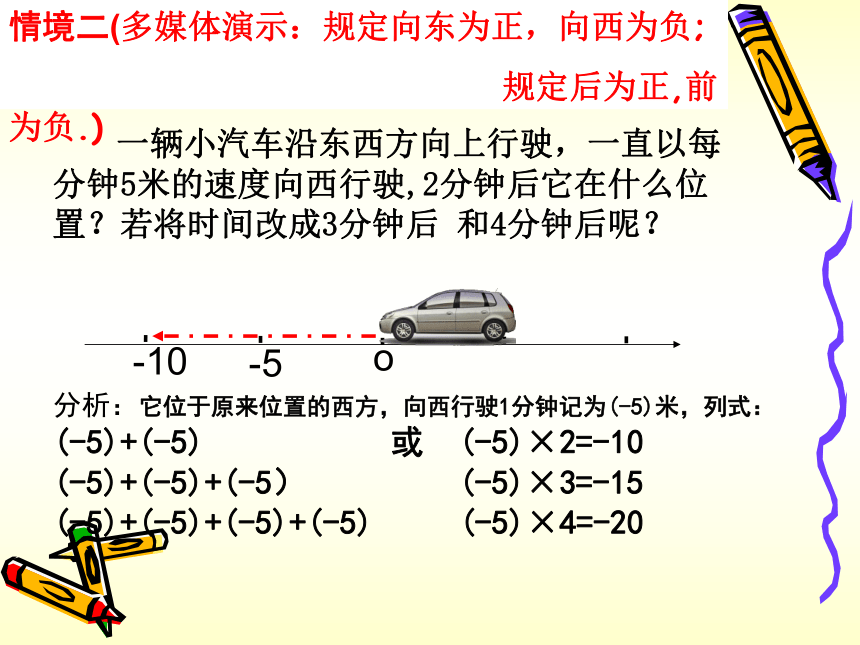
规定后为正,前为负.) 一辆小汽车沿东西方向上行驶,一直以每分钟5米的速度向西行驶,2分钟后它在什么位置?若将时间改成3分钟后 和4分钟后呢? 分析:它位于原来位置的西方,向西行驶1分钟记为(-5)米,列式:
(-5)+(-5) 或 (-5)×2=-10
(-5)+(-5)+(-5) (-5)×3=-15
(-5)+(-5)+(-5)+(-5) (-5)×4=-20-10-5情境二(多媒体演示:规定向东为正,向西为负;
规定后为正,前为负.)o-5-10 一辆小汽车沿东西方向上行驶,一直以每分钟5米的速度向东行驶,2分钟前它在什么位置? 若将时间改成3分钟前和4分钟前呢? 分析:它位于原来位置的东方,相距:
5+5=10 或 5×(-2)=-10
5+5+5=15 5×(-3)=-15
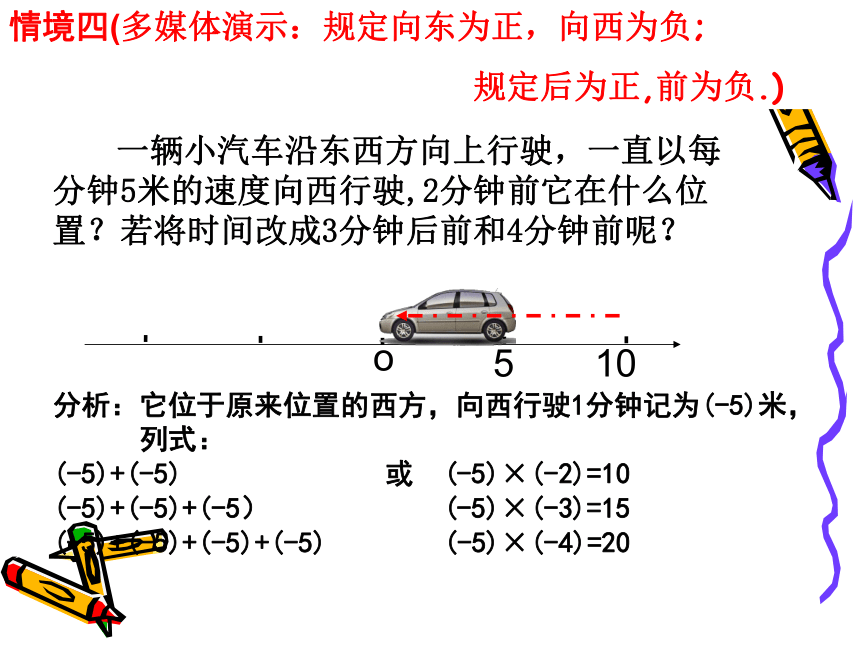
5+5+5+5=20 5×(-4)=-20情境三(多媒体演示:规定向东为正,向西为负; 规定后为正,前为负.) 一辆小汽车沿东西方向上行驶,一直以每分钟5米的速度向西行驶,2分钟前它在什么位置?若将时间改成3分钟后前和4分钟前呢? 分析:它位于原来位置的西方,向西行驶1分钟记为(-5)米,
列式:
(-5)+(-5) 或 (-5)×(-2)=10
(-5)+(-5)+(-5) (-5)×(-3)=15
(-5)+(-5)+(-5)+(-5) (-5)×(-4)=20105情境四(多媒体演示:规定向东为正,向西为负;
规定后为正,前为负.)5 × 2 = 10
5 × 3 = 15
5 × 4 = 20(-5) × 2 = -10
(-5) × 3 = -15
(-5) × 4 = -205 × (-2) = -10
5 × (-3) = -15
5 × (-4) = -20(-5) ×(-2) = 10
(-5) ×(-3) = 15
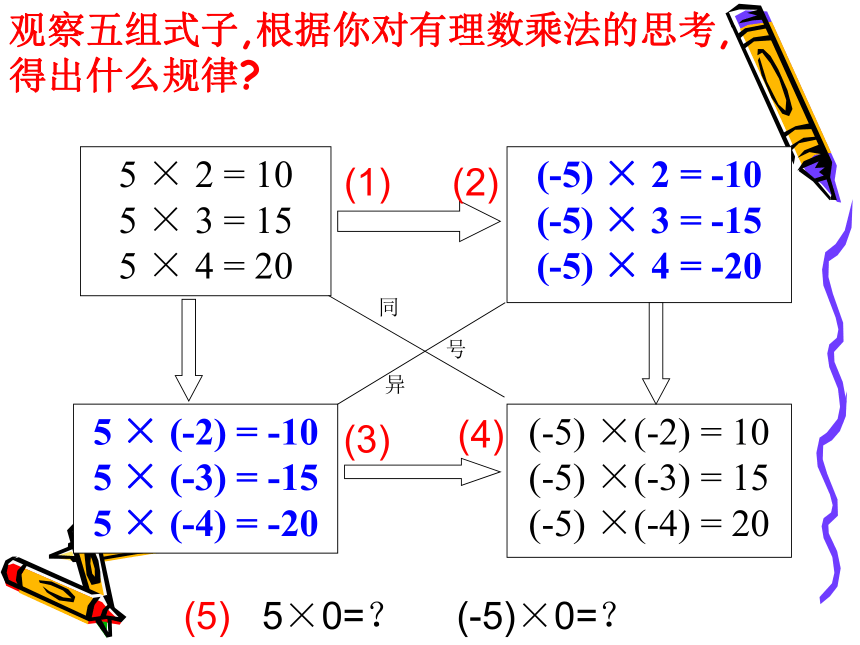
(-5) ×(-4) = 20(5) 5×0=? (-5)×0=?(1)(2)(3)(4)同号异观察五组式子,根据你对有理数乘法的思考,
得出什么规律?有理数乘法(multiplication)法则两数相乘,同号得正,异号得负,绝对值相乘。
任何数与0相乘,积仍为0。结合法则,让学生观察下面两个式子:
(1) (-5)×(-2) = + (5×2) = +10;
(2) (-5) × 2 = - (5×2) = -10
从中你发现有理数乘法运算与小学乘法运算有什么联系吗?同号两数相乘得正把绝对值相乘异号两数相乘得负把绝对值相乘理解法则,掌握实质 (1)先确定积的符号;
(2)将每个因数的绝对值求积作为积的绝对值。
确定积的符号步骤:关键:同号得正,异号得负有理数乘法例: 计算
(1)小题由学生完成,(2)小题由教师示范
(1) (-3)×9 (2) (- ) ×(-2)
应用法则,知识迁移1、突破能力层
(1)1×1 (2) (-1)×(-1) (3) ×3
(4) - ×(-3) (5) a× (a≠0)
前面做得很好,继续努力,一定行! 想一想,从计算结果中,你发现有何规律?快乐套餐有理数倒数的概念乘积是1的两个有理数互为倒数。注意:用式子表示:如果ab=1,则a、b互为倒数;反之,如果a、b互为倒数,则ab=1求倒数与符号无关,不能改变符号。思考:谁的倒数等于它本身?
0有倒数吗?
一个整数,分数,带分数,小数的倒数怎么求?±1没有练习1,写出下列各数的倒数。变式:3. 下列说法错误的是( )
A. 小于-1的数的倒数大于其本身。
B. 大于-1的数的倒数小于其本身
C. 一个数的倒数不能等于它本身。
D. 1和-1互为负倒数。C两个有理数相乘,先要确定积的符号,然后再确定积的绝对值,那三个有理数相乘怎样呢?填空 (1) 4×5×0.25=?
(2) (-4)×5×0.25=?
(3) (-4)×(-5)×0.25=?
(4) (-4)×(-5)×(-0.25)=?
(5)(-4)×5×(-0.25)×0=?思考:5-55-50想一想,从计算结果中,积的符号又怎样确定呢?
积的绝对值是多少?几个不等于0的因数相乘,积的符号由负因数的个数决定。当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正。只要有一个因数为0,积就为0。多个有理数相乘的法则积的绝对值是这几个因数的绝对值的乘积 把-6表示成两个整数的积, 有多少种可能性?把它们全部写出来。例?计算练习(2) (-2) ×3×(-0.5)(3) |-1.25| ×(-8) ×4探索活动:4)乘积是1的两个有理数互为倒数。课堂小结通过本节课的学习,大家学会了什么?(1)有理数的乘法法则。(2)多个不等于0的有理数相乘,积的符号
由负因数的个数决定。(3)几个数相乘时,如果有一个因数是0,则积就为0。开放性试题1.当 a、b是什么有理数时,等式|ab|=-ab成立。解:(1)当a>0, b<0时, 等式|ab|=-ab;
(2) 当a<0, b>0时, 等式|ab|=-ab;
(3) 当a、b两数中至少有一个数为0时,等式|ab|=-ab;变式:当 a、b是什么有理数时,等式ab= |ab|成立。解:(1)当a>0, b>0时, 等式ab =|ab|
(2) 当a<0, b<0时, 等式ab =|ab|
(3) 当a、b两数中至少有一个数为0时,等式|ab|=-ab;一题多变,越变越聪明例:已知|x|=2, |y|=3,且x y<0,求x 、y的值?变式1:已知|x|=2, |y|=3,且x y>0,求x 、y的值?变式2:已知|x|=2, |y|=3,且x y<0,求|2x-3y|的值?变式3:已知|x|=2, |y|=3,且x y>0,求|x+y|- |x-y|的值?自主探究题1.计算下列各式,将其结果填在 横线上.
15×15=______ 27×23=______
34×36=______ 71×79=______(1)你发现了什么?
(2)你能直接写出一个- 98×92的结果吗?22562112245609答:两个因数的十位数字相同,个位数字之和为10,
它们的积为: 十位数字×(十位数字+1) ×100+个位数字的积解:- 98×92=-9016自主探究题2. 三个正方体木块粘合成如图所示的模型,它们的棱长分别为1米,2米,3米,要在模型上涂油漆,如果除去粘合部分不涂外,求模型的涂漆面积.解:涂漆面积相当于棱长为3米的立方体的六个面,棱长为2米的正方体的4个面与棱长为米的正方体的4个面,涂漆面积为3×3×6+2×2×4+1×1×4=74(平方米)谢谢!
5+5=10 或 5×2=10
5+5+5=15 5×3=15
5+5+5+5=20 5×4=20情境一(多媒体演示:规定向东为正,向西为负;
规定后为正,前为负.) 一辆小汽车沿东西方向上行驶,一直以每分钟5米的速度向西行驶,2分钟后它在什么位置?若将时间改成3分钟后 和4分钟后呢? 分析:它位于原来位置的西方,向西行驶1分钟记为(-5)米,列式:
(-5)+(-5) 或 (-5)×2=-10
(-5)+(-5)+(-5) (-5)×3=-15
(-5)+(-5)+(-5)+(-5) (-5)×4=-20-10-5情境二(多媒体演示:规定向东为正,向西为负;
规定后为正,前为负.)o-5-10 一辆小汽车沿东西方向上行驶,一直以每分钟5米的速度向东行驶,2分钟前它在什么位置? 若将时间改成3分钟前和4分钟前呢? 分析:它位于原来位置的东方,相距:
5+5=10 或 5×(-2)=-10
5+5+5=15 5×(-3)=-15
5+5+5+5=20 5×(-4)=-20情境三(多媒体演示:规定向东为正,向西为负; 规定后为正,前为负.) 一辆小汽车沿东西方向上行驶,一直以每分钟5米的速度向西行驶,2分钟前它在什么位置?若将时间改成3分钟后前和4分钟前呢? 分析:它位于原来位置的西方,向西行驶1分钟记为(-5)米,
列式:
(-5)+(-5) 或 (-5)×(-2)=10
(-5)+(-5)+(-5) (-5)×(-3)=15
(-5)+(-5)+(-5)+(-5) (-5)×(-4)=20105情境四(多媒体演示:规定向东为正,向西为负;
规定后为正,前为负.)5 × 2 = 10
5 × 3 = 15
5 × 4 = 20(-5) × 2 = -10
(-5) × 3 = -15
(-5) × 4 = -205 × (-2) = -10
5 × (-3) = -15
5 × (-4) = -20(-5) ×(-2) = 10
(-5) ×(-3) = 15
(-5) ×(-4) = 20(5) 5×0=? (-5)×0=?(1)(2)(3)(4)同号异观察五组式子,根据你对有理数乘法的思考,
得出什么规律?有理数乘法(multiplication)法则两数相乘,同号得正,异号得负,绝对值相乘。
任何数与0相乘,积仍为0。结合法则,让学生观察下面两个式子:
(1) (-5)×(-2) = + (5×2) = +10;
(2) (-5) × 2 = - (5×2) = -10
从中你发现有理数乘法运算与小学乘法运算有什么联系吗?同号两数相乘得正把绝对值相乘异号两数相乘得负把绝对值相乘理解法则,掌握实质 (1)先确定积的符号;
(2)将每个因数的绝对值求积作为积的绝对值。
确定积的符号步骤:关键:同号得正,异号得负有理数乘法例: 计算
(1)小题由学生完成,(2)小题由教师示范
(1) (-3)×9 (2) (- ) ×(-2)
应用法则,知识迁移1、突破能力层
(1)1×1 (2) (-1)×(-1) (3) ×3
(4) - ×(-3) (5) a× (a≠0)
前面做得很好,继续努力,一定行! 想一想,从计算结果中,你发现有何规律?快乐套餐有理数倒数的概念乘积是1的两个有理数互为倒数。注意:用式子表示:如果ab=1,则a、b互为倒数;反之,如果a、b互为倒数,则ab=1求倒数与符号无关,不能改变符号。思考:谁的倒数等于它本身?
0有倒数吗?
一个整数,分数,带分数,小数的倒数怎么求?±1没有练习1,写出下列各数的倒数。变式:3. 下列说法错误的是( )
A. 小于-1的数的倒数大于其本身。
B. 大于-1的数的倒数小于其本身
C. 一个数的倒数不能等于它本身。
D. 1和-1互为负倒数。C两个有理数相乘,先要确定积的符号,然后再确定积的绝对值,那三个有理数相乘怎样呢?填空 (1) 4×5×0.25=?
(2) (-4)×5×0.25=?
(3) (-4)×(-5)×0.25=?
(4) (-4)×(-5)×(-0.25)=?
(5)(-4)×5×(-0.25)×0=?思考:5-55-50想一想,从计算结果中,积的符号又怎样确定呢?
积的绝对值是多少?几个不等于0的因数相乘,积的符号由负因数的个数决定。当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正。只要有一个因数为0,积就为0。多个有理数相乘的法则积的绝对值是这几个因数的绝对值的乘积 把-6表示成两个整数的积, 有多少种可能性?把它们全部写出来。例?计算练习(2) (-2) ×3×(-0.5)(3) |-1.25| ×(-8) ×4探索活动:4)乘积是1的两个有理数互为倒数。课堂小结通过本节课的学习,大家学会了什么?(1)有理数的乘法法则。(2)多个不等于0的有理数相乘,积的符号
由负因数的个数决定。(3)几个数相乘时,如果有一个因数是0,则积就为0。开放性试题1.当 a、b是什么有理数时,等式|ab|=-ab成立。解:(1)当a>0, b<0时, 等式|ab|=-ab;
(2) 当a<0, b>0时, 等式|ab|=-ab;
(3) 当a、b两数中至少有一个数为0时,等式|ab|=-ab;变式:当 a、b是什么有理数时,等式ab= |ab|成立。解:(1)当a>0, b>0时, 等式ab =|ab|
(2) 当a<0, b<0时, 等式ab =|ab|
(3) 当a、b两数中至少有一个数为0时,等式|ab|=-ab;一题多变,越变越聪明例:已知|x|=2, |y|=3,且x y<0,求x 、y的值?变式1:已知|x|=2, |y|=3,且x y>0,求x 、y的值?变式2:已知|x|=2, |y|=3,且x y<0,求|2x-3y|的值?变式3:已知|x|=2, |y|=3,且x y>0,求|x+y|- |x-y|的值?自主探究题1.计算下列各式,将其结果填在 横线上.
15×15=______ 27×23=______
34×36=______ 71×79=______(1)你发现了什么?
(2)你能直接写出一个- 98×92的结果吗?22562112245609答:两个因数的十位数字相同,个位数字之和为10,
它们的积为: 十位数字×(十位数字+1) ×100+个位数字的积解:- 98×92=-9016自主探究题2. 三个正方体木块粘合成如图所示的模型,它们的棱长分别为1米,2米,3米,要在模型上涂油漆,如果除去粘合部分不涂外,求模型的涂漆面积.解:涂漆面积相当于棱长为3米的立方体的六个面,棱长为2米的正方体的4个面与棱长为米的正方体的4个面,涂漆面积为3×3×6+2×2×4+1×1×4=74(平方米)谢谢!
