河北省唐山市丰南一中2013-2014学年高二上学期第一次阶段考试数学试题(文)
文档属性
| 名称 | 河北省唐山市丰南一中2013-2014学年高二上学期第一次阶段考试数学试题(文) |  | |
| 格式 | zip | ||
| 文件大小 | 311.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-11 16:06:19 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
丰南一中2013-2014学年高二上学期第一次阶段考试
数学文
一.选择题(每个选项只有一个正确答案,每小题5分,共60分)
1、已知平面α内有无数条直线都与平面β平行,那么( )
A.α∥β B.α与β相交 C.α与β重合 D.α∥β或α与β相交
2.下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是 ( )
A.(1)(2) B.(2)(3) C.(3)(4) D.(1)(4)
3. 设、是两条不同的直线,是一个平面,则下列命题正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
4. 已知两条直线,和平面,且,则与的位置关系是( ) A.平面 B.平面
C.平面 D.平面,或平面
5、下列说法正确的是
A、三点确定一个平面 B、四边形一定是平面图形
C、梯形一定是平面图形 D、平面和平面有不同在一条直线上的三个交点
6、在空间四边形各边上分别取四点,如果与能相交于点,那么 ( )
A、点必在直线上 B、点必在直线BD上
C、点必在平面内 D、点必在平面内
7.三个平面把空间分成7部分时,它们的交线有( )
A.1条 B.2条 C.3条 D.1条或2条
8.如图所示,一个空间几何体的正视图和侧视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的全面积为:
A、 B、 C、 D、
9、有下列命题:①有两个面平行,其余各面都是四边形的几何体叫棱柱;②有两个面平行, 其余各面都是平行四边形的几何体叫棱柱; ③有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱;④ 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台。⑤有一个面是多边形,其余各面都是三角形的几何体是棱锥。其中正确的命题的个数为 ( )
A. B. C. D.
10、圆锥母线长为1,侧面展开图的圆心角为240°,则圆锥体积为( )
A. B. C. D.
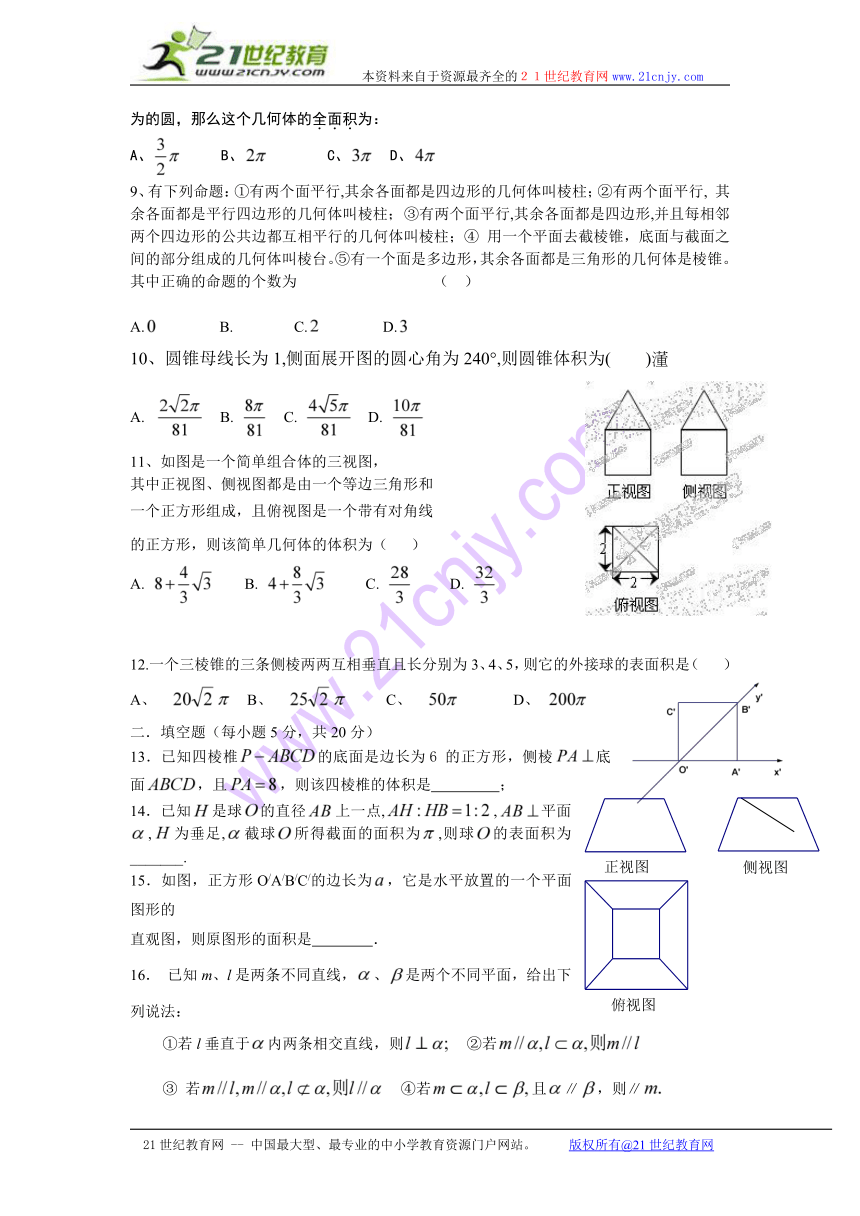
11、如图是一个简单组合体的三视图,
其中正视图、侧视图都是由一个等边三角形和
一个正方形组成,且俯视图是一个带有对角线
的正方形,则该简单几何体的体积为( )
A. B. C. D.
12.一个三棱锥的三条侧棱两两互相垂直且长分别为3、4、5,则它的外接球的表面积是( )
A、 B、 C、 D、
二.填空题(每小题5分,共20分)
13.已知四棱椎的底面是边长为6 的正方形,侧棱底面,且,则该四棱椎的体积是 ;
14.已知是球的直径上一点,,平面,为垂足,截球所得截面的面积为,则球的表面积为_______.
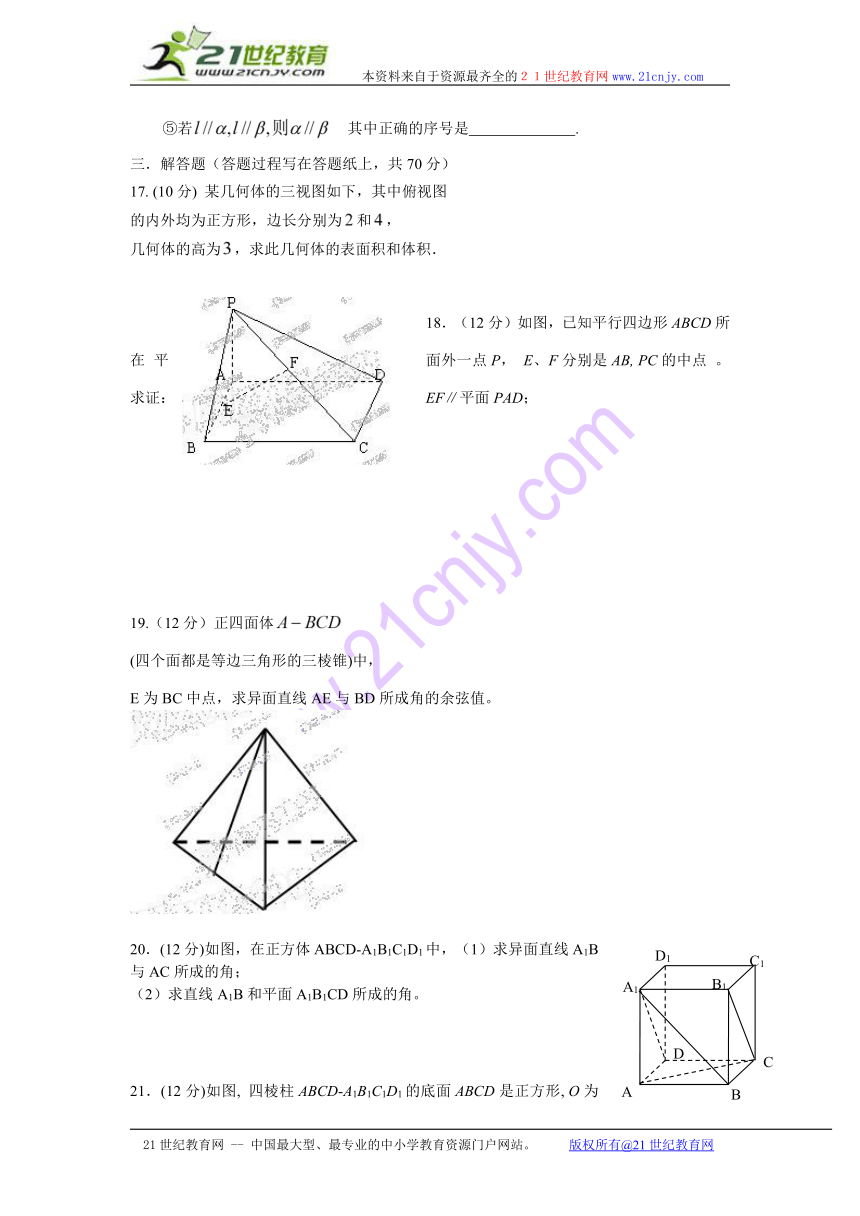
15.如图,正方形O/A/B/C/的边长为,它是水平放置的一个平面图形的
直观图,则原图形的面积是 .
16. 已知m、l是两条不同直线,、是两个不同平面,给出下列说法:
①若l垂直于内两条相交直线,则 ②若
③ 若 ④若且∥,则∥
⑤若 其中正确的序号是 .
三.解答题(答题过程写在答题纸上,共70分)
17. (10分) 某几何体的三视图如下,其中俯视图
的内外均为正方形,边长分别为和,
几何体的高为,求此几何体的表面积和体积.
18.(12分)如图,已知平行四边形ABCD所在平面外一点P, E、F分别是AB, PC的中点 。求证:EF∥平面PAD;
19.(12分)正四面体
(四个面都是等边三角形的三棱锥)中,
E为BC中点,求异面直线AE与BD所成角的余弦值。
20.(12分)如图,在正方体ABCD-A1B1C1D1中,(1)求异面直线A1B与AC所成的角;
(2)求直线A1B和平面A1B1CD所成的角。
21.(12分)如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, .
(Ⅰ) 证明: A1BD // 平面CD1B1; (Ⅱ) 求三棱柱ABD-A1B1D1的体积.
22. (本小题满分12分)如图,在四棱锥中,,,且DB平分,E为PC的中点,,
(Ⅰ)证明
(Ⅱ)证明
(Ⅲ)求直线BC与平面PBD所成的角的正切值
2013-2014学年度第一学期丰南一中高二
第一次阶段考试数学试卷
答案(文理合并)
20.解: (Ⅰ) 设.
.
21.证:连AC,设AC中点为O,连OF、OE(1)在△PAC中,∵ F、O分别为PC、AC的中点 ∴ FO∥PA …………①在△ABC中,
∵ E、O分别为AB、AC的中点
∴ EO∥BC ,又
∵ BC∥AD ∴ EO∥AD …………②
综合①、②可知:平面EFO∥平面PAD ∵ EF 平面EFO
∴ EF∥平面PAD.
22.解析: (1)证明:如图,连接BD,MO,在平行四边形ABCD中,因为O为AC的中点,所以O为BD的中点.
又M为PD的中点,所以PB∥MO.因为PB 平面ACM,MO 平面ACM,所以PB∥平面ACM.
即直线AM与平面ABCD所成角的正切值为.
俯视图
俯视图
侧视图
正视图
A
A1
B
B1
C1
D1
C
D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
丰南一中2013-2014学年高二上学期第一次阶段考试
数学文
一.选择题(每个选项只有一个正确答案,每小题5分,共60分)
1、已知平面α内有无数条直线都与平面β平行,那么( )
A.α∥β B.α与β相交 C.α与β重合 D.α∥β或α与β相交
2.下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是 ( )
A.(1)(2) B.(2)(3) C.(3)(4) D.(1)(4)
3. 设、是两条不同的直线,是一个平面,则下列命题正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
4. 已知两条直线,和平面,且,则与的位置关系是( ) A.平面 B.平面
C.平面 D.平面,或平面
5、下列说法正确的是
A、三点确定一个平面 B、四边形一定是平面图形
C、梯形一定是平面图形 D、平面和平面有不同在一条直线上的三个交点
6、在空间四边形各边上分别取四点,如果与能相交于点,那么 ( )
A、点必在直线上 B、点必在直线BD上
C、点必在平面内 D、点必在平面内
7.三个平面把空间分成7部分时,它们的交线有( )
A.1条 B.2条 C.3条 D.1条或2条
8.如图所示,一个空间几何体的正视图和侧视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的全面积为:
A、 B、 C、 D、
9、有下列命题:①有两个面平行,其余各面都是四边形的几何体叫棱柱;②有两个面平行, 其余各面都是平行四边形的几何体叫棱柱; ③有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱;④ 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台。⑤有一个面是多边形,其余各面都是三角形的几何体是棱锥。其中正确的命题的个数为 ( )
A. B. C. D.
10、圆锥母线长为1,侧面展开图的圆心角为240°,则圆锥体积为( )
A. B. C. D.
11、如图是一个简单组合体的三视图,
其中正视图、侧视图都是由一个等边三角形和
一个正方形组成,且俯视图是一个带有对角线
的正方形,则该简单几何体的体积为( )
A. B. C. D.
12.一个三棱锥的三条侧棱两两互相垂直且长分别为3、4、5,则它的外接球的表面积是( )
A、 B、 C、 D、
二.填空题(每小题5分,共20分)
13.已知四棱椎的底面是边长为6 的正方形,侧棱底面,且,则该四棱椎的体积是 ;
14.已知是球的直径上一点,,平面,为垂足,截球所得截面的面积为,则球的表面积为_______.
15.如图,正方形O/A/B/C/的边长为,它是水平放置的一个平面图形的
直观图,则原图形的面积是 .
16. 已知m、l是两条不同直线,、是两个不同平面,给出下列说法:
①若l垂直于内两条相交直线,则 ②若
③ 若 ④若且∥,则∥
⑤若 其中正确的序号是 .
三.解答题(答题过程写在答题纸上,共70分)
17. (10分) 某几何体的三视图如下,其中俯视图
的内外均为正方形,边长分别为和,
几何体的高为,求此几何体的表面积和体积.
18.(12分)如图,已知平行四边形ABCD所在平面外一点P, E、F分别是AB, PC的中点 。求证:EF∥平面PAD;
19.(12分)正四面体
(四个面都是等边三角形的三棱锥)中,
E为BC中点,求异面直线AE与BD所成角的余弦值。
20.(12分)如图,在正方体ABCD-A1B1C1D1中,(1)求异面直线A1B与AC所成的角;
(2)求直线A1B和平面A1B1CD所成的角。
21.(12分)如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, .
(Ⅰ) 证明: A1BD // 平面CD1B1; (Ⅱ) 求三棱柱ABD-A1B1D1的体积.
22. (本小题满分12分)如图,在四棱锥中,,,且DB平分,E为PC的中点,,
(Ⅰ)证明
(Ⅱ)证明
(Ⅲ)求直线BC与平面PBD所成的角的正切值
2013-2014学年度第一学期丰南一中高二
第一次阶段考试数学试卷
答案(文理合并)
20.解: (Ⅰ) 设.
.
21.证:连AC,设AC中点为O,连OF、OE(1)在△PAC中,∵ F、O分别为PC、AC的中点 ∴ FO∥PA …………①在△ABC中,
∵ E、O分别为AB、AC的中点
∴ EO∥BC ,又
∵ BC∥AD ∴ EO∥AD …………②
综合①、②可知:平面EFO∥平面PAD ∵ EF 平面EFO
∴ EF∥平面PAD.
22.解析: (1)证明:如图,连接BD,MO,在平行四边形ABCD中,因为O为AC的中点,所以O为BD的中点.
又M为PD的中点,所以PB∥MO.因为PB 平面ACM,MO 平面ACM,所以PB∥平面ACM.
即直线AM与平面ABCD所成角的正切值为.
俯视图
俯视图
侧视图
正视图
A
A1
B
B1
C1
D1
C
D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
