2022—2023学年人教版数学八年级上册14.2.2 完全平方公式 课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册14.2.2 完全平方公式 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
14.2.2 完全平方公式
第十四章 整式的乘法与因式分解
14.2 乘法公式
学习目标
理解完全平方公式,能运用公式进行计算;
会用一般到特殊的研究问题的方法探索完全平方公式,会用数形结合的思想解释完全平方公式。
理解完全平方公式的结构与特征,能正确的运用公式进行计算(重点)
完全平方公式的变式运用(难点)
教学重难点
情境引入
八年级一班共49人,现需要购进一批班服,一件班服的价格也是49元,请问共需要多少元,小明很快的就得出了答案,你知道小明是怎样迅速得到答案的吗?
49×49
问题1: 计算下列多项式的积,你能发现什么规律?
(1) (x+p)(x+q)=
问题2:根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
探究一
追问①当p=q时(x+p)(x+p)=
当 p=q=2时(x+2)(x+2)=
(x-p)(x-q)=
追问② 当p=q时(x-p)(x-p)=
当 p=q=2时 (x-2)(x-2)=
有一块边长为a米的正方形土地,现要扩大这片土地面积,两位同学提出了两种不同的方案,甲:边长增加b米;乙:增加一块边长为b的正方形,这时候面积跟甲的增加后的面积一样大了。你认为乙的说法对吗,谁的方案最后得到的面积最大?
探究二
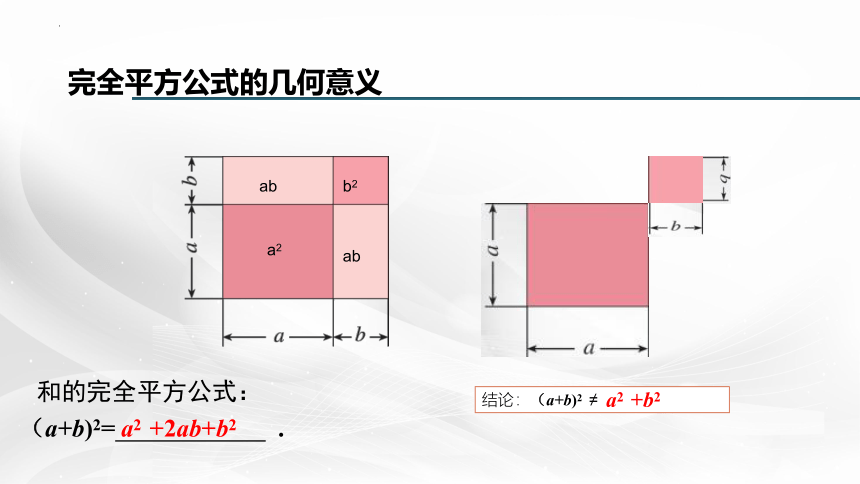
完全平方公式的几何意义
(a+b)2= .
a2 +2ab+b2
和的完全平方公式:
结论:(a+b)2
≠
a2 +b2
ab
b2
ab
a2
(a-b)2= .
a2-2ab+b2
差的完全平方公式:
Ⅳ
Ⅰ
Ⅱ
Ⅲ
a
a
b
b
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
简记为“首平方,尾平方,积的2倍放中间”
结构特征:
1、积为二次三项式;
2、积中两项为两数的平方和,另一项为两数积的2倍;
3、字母a,b可以表示数、单项式和多项式
文字表述
公式要点总结
公式表达
例1 运用完全平方公式计算:
典例精析
1、练一练:利用完全平方公式计算:
针对训练
2、想一想:下面各式的计算是否正确?如果不正确,应当怎样改正?
针对训练
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x-y)2 =4x2 -2xy -y2
×
×
×
×
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(-x +y)2 =x2 -2xy +y2
(2x -y)2 =4x2-4xy +y2
(1) 1022;
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
992
= (100 –1)2
=10000 -200+1
=9801.
3、用一用:运用完全平方公式计算:
方法总结:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
针对训练
1、如果x2+kx+81是运用完全平方式得到的结果,
则k=______
18或-18
变式:如果x2+6x+m2是完全平方式,则m的值是_____
3或-3
拓展训练
2、已知ab=2,(a+b)2=9,则(a-b)2的值为______
变式:若题目条件不变,则a-b的值为_____
±1
1
3.下列计算结果为2ab-a2-b2的是( )
A.(a-b)2 B.(-a-b)2
C.-(a+b)2 D.-(a-b)2
D
拓展训练
数学知识
数学思想、方法
数形结合
一般到特殊
具体到抽象
完全平方公式推导及应用
设计意图:知识梳理,体会知识间的联系,提炼数学思想
课堂小结,整体回顾
公式表达
易错点及常见变形
感谢您的聆听
14.2.2 完全平方公式
第十四章 整式的乘法与因式分解
14.2 乘法公式
学习目标
理解完全平方公式,能运用公式进行计算;
会用一般到特殊的研究问题的方法探索完全平方公式,会用数形结合的思想解释完全平方公式。
理解完全平方公式的结构与特征,能正确的运用公式进行计算(重点)
完全平方公式的变式运用(难点)
教学重难点
情境引入
八年级一班共49人,现需要购进一批班服,一件班服的价格也是49元,请问共需要多少元,小明很快的就得出了答案,你知道小明是怎样迅速得到答案的吗?
49×49
问题1: 计算下列多项式的积,你能发现什么规律?
(1) (x+p)(x+q)=
问题2:根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
探究一
追问①当p=q时(x+p)(x+p)=
当 p=q=2时(x+2)(x+2)=
(x-p)(x-q)=
追问② 当p=q时(x-p)(x-p)=
当 p=q=2时 (x-2)(x-2)=
有一块边长为a米的正方形土地,现要扩大这片土地面积,两位同学提出了两种不同的方案,甲:边长增加b米;乙:增加一块边长为b的正方形,这时候面积跟甲的增加后的面积一样大了。你认为乙的说法对吗,谁的方案最后得到的面积最大?
探究二
完全平方公式的几何意义
(a+b)2= .
a2 +2ab+b2
和的完全平方公式:
结论:(a+b)2
≠
a2 +b2
ab
b2
ab
a2
(a-b)2= .
a2-2ab+b2
差的完全平方公式:
Ⅳ
Ⅰ
Ⅱ
Ⅲ
a
a
b
b
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
简记为“首平方,尾平方,积的2倍放中间”
结构特征:
1、积为二次三项式;
2、积中两项为两数的平方和,另一项为两数积的2倍;
3、字母a,b可以表示数、单项式和多项式
文字表述
公式要点总结
公式表达
例1 运用完全平方公式计算:
典例精析
1、练一练:利用完全平方公式计算:
针对训练
2、想一想:下面各式的计算是否正确?如果不正确,应当怎样改正?
针对训练
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x-y)2 =4x2 -2xy -y2
×
×
×
×
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(-x +y)2 =x2 -2xy +y2
(2x -y)2 =4x2-4xy +y2
(1) 1022;
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
992
= (100 –1)2
=10000 -200+1
=9801.
3、用一用:运用完全平方公式计算:
方法总结:运用完全平方公式进行简便计算,要熟记完全平方公式的特征,将原式转化为能利用完全平方公式的形式.
针对训练
1、如果x2+kx+81是运用完全平方式得到的结果,
则k=______
18或-18
变式:如果x2+6x+m2是完全平方式,则m的值是_____
3或-3
拓展训练
2、已知ab=2,(a+b)2=9,则(a-b)2的值为______
变式:若题目条件不变,则a-b的值为_____
±1
1
3.下列计算结果为2ab-a2-b2的是( )
A.(a-b)2 B.(-a-b)2
C.-(a+b)2 D.-(a-b)2
D
拓展训练
数学知识
数学思想、方法
数形结合
一般到特殊
具体到抽象
完全平方公式推导及应用
设计意图:知识梳理,体会知识间的联系,提炼数学思想
课堂小结,整体回顾
公式表达
易错点及常见变形
感谢您的聆听
