浙江省金华一中2013-2014学年高一入学摸底数学试卷
文档属性
| 名称 | 浙江省金华一中2013-2014学年高一入学摸底数学试卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 88.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-11 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
金华一中高一新生摸底考试数学试题
注意:答案必须写在答题卷上
一、选择题:本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,那么( )
A. B. C. D.
2.设,则a,b,c大小关系 ( )
A.a>c>b B.a>b>c C. c>a>b D.b>a>c
3.已知集合,下列从A到B的对应关系f不是映射的是( )
A. B.
C. D.
4.下列函数中与函数相同的是 ( )
A. B. C. D.
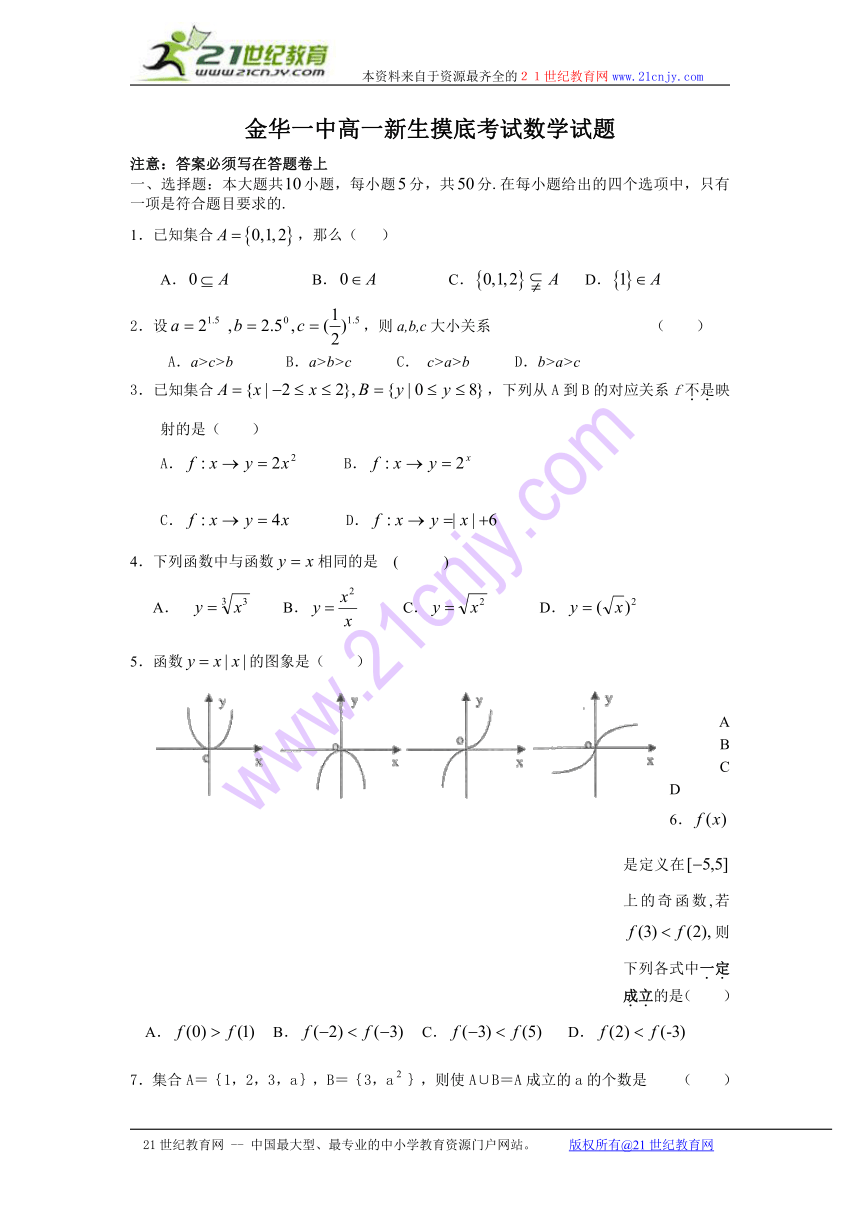
5.函数的图象是( )
A B C D
6.是定义在上的奇函数,若则下列各式中一定成立的是( )
A. B. C. D.
7.集合A={1,2,3,a},B={3,a},则使A∪B=A成立的a的个数是 ( )
A.2个 B.3个 C.4个 D. 5个
8.已知偶函数,当时,,若,则实数的取值范围是( )
A. B. C. D.
9.对任意实数,定义运算,其中是常数,等式右边的运算是通常的加法和乘法运算.已知,并且有一个非零常数,使得对任意实数,都有,则的值是 ( )
A. B. C. D.
10.已知函数,若存在,,使成立,则实数的取值范围是 ( )
A. B. C.或 D.或
二、填空题(本大题共7小题,每小题4分,共28分)
11.函数的定义域为 .
12.已知函数,则= .
13.若函数满足,则
14.已知指数函数在内是增函数,则实数的取值范围是 .
15.已知函数,若,则 .
16.当时,关于x的不等式恒成立,则实数的取值范围是 .
17.设表示不超过的最大整数,如,若函数,则的值域为 .
三、解答题:本题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分14分)化简或求值:
(Ⅰ);
(Ⅱ)
19.(本小题满分14分)已知全集U=R,集合,.
(Ⅰ)分别求,;
(Ⅱ)已知,若,求实数的取值范围.
20.(本小题满分15分)已知函数是奇函数,且.
(Ⅰ)求实数的值;
(Ⅱ)判断函数的单调性,并用函数单调性的定义加以证明;
(Ⅲ)求不等式的解.
21.(本小题满分15分)设函数
(Ⅰ)若表达式;
(Ⅱ)在(Ⅰ)的条件下, (,其中常数),区间D为的值域,若D的长度为,求此时的值。
注:b-a为区间[a,b]的长度
22.(本小题满分14分)已知函数,,。
(Ⅰ)当时,若在上单调递增,求实数的取值范围;
(Ⅱ)求满足下列条件的所有实数对:当是整数时,存在,使得是的最大值,是的最小值.
金华一中高一新生摸底考试数学试题答案
一、BBCAC BCDAD
二、; 3 -1 a>1 -2 {-1,0}
三、18.(本题14分)
解: (Ⅰ)19 (Ⅱ)
19. (Ⅰ);
(Ⅱ)
20.解:(Ⅰ)是定义域为的奇函数,
,经检验符合题意.…………………..4分
(Ⅱ),又且 ………………..6分
用定义可以证明在上单调递增. ………………..10分
(Ⅲ) 原不等式化为
,即
x>1或 x<-4…..15分
21.(本题15分)解(1)a=0时,不能恒成立,--------2分
a≠0时
------------6分
(2),23-2m=
①当时,23-2m==,得: -----10分
②当时,23-2m=,得(舍) ----------12分
③当时,23-2m=,得:
-------------14分
综合得 -- ----15分
22.(本小题满分14分) (Ⅰ)时,,则在上单调递减,不符题意。
时,要使在上单调递增,必须满足 ,∴ 。
综上,。
(Ⅱ)若,,则无最大值,故,
∴为二次函数,
要使有最大值,必须满足,即且,
此时,时,有最大值。
又取最小值时,,依题意,有,
则,
∵且,∴,得,
此时或。
∴满足条件的实数对是。
牛哥@的小弟%上传
21!世纪*教育#网……版权+|有所
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
金华一中高一新生摸底考试数学试题
注意:答案必须写在答题卷上
一、选择题:本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,那么( )
A. B. C. D.
2.设,则a,b,c大小关系 ( )
A.a>c>b B.a>b>c C. c>a>b D.b>a>c
3.已知集合,下列从A到B的对应关系f不是映射的是( )
A. B.
C. D.
4.下列函数中与函数相同的是 ( )
A. B. C. D.
5.函数的图象是( )
A B C D
6.是定义在上的奇函数,若则下列各式中一定成立的是( )
A. B. C. D.
7.集合A={1,2,3,a},B={3,a},则使A∪B=A成立的a的个数是 ( )
A.2个 B.3个 C.4个 D. 5个
8.已知偶函数,当时,,若,则实数的取值范围是( )
A. B. C. D.
9.对任意实数,定义运算,其中是常数,等式右边的运算是通常的加法和乘法运算.已知,并且有一个非零常数,使得对任意实数,都有,则的值是 ( )
A. B. C. D.
10.已知函数,若存在,,使成立,则实数的取值范围是 ( )
A. B. C.或 D.或
二、填空题(本大题共7小题,每小题4分,共28分)
11.函数的定义域为 .
12.已知函数,则= .
13.若函数满足,则
14.已知指数函数在内是增函数,则实数的取值范围是 .
15.已知函数,若,则 .
16.当时,关于x的不等式恒成立,则实数的取值范围是 .
17.设表示不超过的最大整数,如,若函数,则的值域为 .
三、解答题:本题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分14分)化简或求值:
(Ⅰ);
(Ⅱ)
19.(本小题满分14分)已知全集U=R,集合,.
(Ⅰ)分别求,;
(Ⅱ)已知,若,求实数的取值范围.
20.(本小题满分15分)已知函数是奇函数,且.
(Ⅰ)求实数的值;
(Ⅱ)判断函数的单调性,并用函数单调性的定义加以证明;
(Ⅲ)求不等式的解.
21.(本小题满分15分)设函数
(Ⅰ)若表达式;
(Ⅱ)在(Ⅰ)的条件下, (,其中常数),区间D为的值域,若D的长度为,求此时的值。
注:b-a为区间[a,b]的长度
22.(本小题满分14分)已知函数,,。
(Ⅰ)当时,若在上单调递增,求实数的取值范围;
(Ⅱ)求满足下列条件的所有实数对:当是整数时,存在,使得是的最大值,是的最小值.
金华一中高一新生摸底考试数学试题答案
一、BBCAC BCDAD
二、; 3 -1 a>1 -2 {-1,0}
三、18.(本题14分)
解: (Ⅰ)19 (Ⅱ)
19. (Ⅰ);
(Ⅱ)
20.解:(Ⅰ)是定义域为的奇函数,
,经检验符合题意.…………………..4分
(Ⅱ),又且 ………………..6分
用定义可以证明在上单调递增. ………………..10分
(Ⅲ) 原不等式化为
,即
x>1或 x<-4…..15分
21.(本题15分)解(1)a=0时,不能恒成立,--------2分
a≠0时
------------6分
(2),23-2m=
①当时,23-2m==,得: -----10分
②当时,23-2m=,得(舍) ----------12分
③当时,23-2m=,得:
-------------14分
综合得 -- ----15分
22.(本小题满分14分) (Ⅰ)时,,则在上单调递减,不符题意。
时,要使在上单调递增,必须满足 ,∴ 。
综上,。
(Ⅱ)若,,则无最大值,故,
∴为二次函数,
要使有最大值,必须满足,即且,
此时,时,有最大值。
又取最小值时,,依题意,有,
则,
∵且,∴,得,
此时或。
∴满足条件的实数对是。
牛哥@的小弟%上传
21!世纪*教育#网……版权+|有所
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
